Intermediate Questions

If people frequently asked more involved questions, then these might be among them!

Skip to the advanced level questions.

What is the "last-scattering surface"?

The early Universe was so hot that all of the matter was ionized. Ionized stuff is extremely good at interacting with radiation (it has a high "cross-section" for scattering a photon), whereas neutral material is almost transparent. Most of the Universe is hydrogen, which was all ionized up until about a million years after the Big Bang. As the Universe expanded it cooled down, so that all it's constituents had less energy. About a million years after the Big Bang protons were able to hold onto electrons, without the energies being so high that the electrons would get torn off again. So the material of the Universe became neutral at that time, after which the photons and hydrogen atoms hardly interacted with each other again. So when we look out into space we see a microwave photon coming from the direction where it last scattered off ionized material. There were ions and electrons in every direction around us, as long as we look out to large enough distances (which means looking far enough into the past, because of the finite speed of light). So we can define a "last-scattering surface", which is a distant shell in space, where today's CMB photons last scattered off ionized matter. Closer than this surface the Universe was essentially transparent. Further away than this surface the photons and ions were rapidly scattering. So although the surface has a finite thickness, it is a relatively sharp boundary. Most of the anisotropies we see on the microwave sky today were generated on this last-scattering surface.

Can I see the objects that caused the anisotropies?

Sometimes people forget that most of the CMB anisotropies are formed on the last scattering surface, Knowing that the precursors of clusters and super-clusters caused the microwave bumps, it's not too hard to get confused about the connection between these objects and local structures. But remember that the last scattering event was around 300,000 years after the Big Bang, ie a very long time ago. So the objects which caused the hot and cold spots, seen by COBE for example, are about 15 billion light years distant (assuming this is the age of the Universe), and we're seeing their effects on the CMB about 15 billion years ago. So the actual structures which caused the microwave ripples are basically at a horizon length from us, and hence far from being the structures that we trace out using relatively nearby clusters. However, in a statistical sense these objects ought to be very similar to what local structures were like about 15 billion years ago. And remember that someone who lives close to a horizon-distance away from us will see our local supercluster causing an anisotropy on their last scattering surface.

Are hot spots over-densities or under-densities?

In the standard theoretical pictures which people have for the CMB fluctuations, the large-angle variations are caused by gravitational red-shifts and blue-shifts from blobs sitting on the last-scattering surface. An overdensity (ie a region with more matter than the average) causes a photon to lose energy on its way out: we say there is a "gravitational redshift" as the photon "climbs out of the potential well". An underdensity on the other hand, leads to a blueshift. Since a redshift means a lower energy (redder) photon, then that corresponds to a slightly lower CMB temperature. So overdensities are cold spots, and underdensities are hot spots.

There are of course alternative theories in which the large angle anisotropies are caused by things slightly different than these simple gravitational redshifts and blueshifts. In such theories it is possible for over- and under-densities to correspond to the opposite from what was described above. In particular in models where the initial perturbations come from "topological defect" or "isocurvature" modes, things can be more complicated. Presumably at some time in the near future we will know definitively what sort of large-scale fluctuations our Universe has, and then we will know for certain whether you can point to a CMB hot spot and say "the Universe used to be slightly under-dense in that direction"!

What is "Cosmic Variance"?

When you try to estimate any quantity based on a restricted sample, then you expect some uncertainty between your estimate and the "true" underlying value. This is sometimes known as the sample or sampling variance. As you build up a bigger and bigger sample you expect this uncertainty to decrease (if everything is behaving nicely, it will go down like the square root of the number of samples).

Now let's imagine that we're trying to determine the value of something on some pretty large scale, say a reasonable fraction of the size of the observable Universe. This quantity may be density or velocity or some such. Then what we will find is that we will eventually run into a limit, because there's only a finite observable Universe, and then we can't get a bigger sample. Things are even clearer for the CMB, if we are trying to determine the power spectrum, or equivalently the amplitudes of some multipole moments (how big the fluctuations are at different angular scales). Any underlying theory will give a prediction for the expectation value of the multipole coefficients, but the density fluctuations are inherently a stochastic process: the theory will not tell us what the realization is in our particular region of spacetime. This leads to an inherent uncertainty in the determination of the theoretical "expectation value" (what you would get if you could average over an ensemble of universes) from our empirically determined quantity. No matter how precisely you measure things, you can't get rid of this "Cosmic Variance".

Take the quadrupole anisotropy as an example. This is a thing on the sky which has five coefficients. Each of those coefficients is some random number (a Gaussian random variate in the standard models), and so the statistical distribution expected for the quadrupole amplitude is like the sum of five Gaussians (a 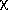² distribution with 5 degrees of freedom), and so is pretty wide. This means that measuring the actual quadrupole on our sky doesn't tell you a whole lot about the expectation value of quadrupoles for a bunch of observers. You can think of this uncertainty as a "theoretical error bar" if you like. For higher multipoles (smaller angular scales) there are a lot more samples, and so the "Cosmic Variance" is less important. So if you're trying to determine the angular power spectrum, then at large angles you tend to be dominated by "Cosmic Variance", while at small angles you're dominated by instrumental noise.