I have a friend who doesn't believe in the expansion of the Universe.
His main argument is that our speed relative to the microwave background
is nowhere near the speed of light, and so we must be at the centre of the
expansion. How do I answer this? And are there any good articles to read?
Submitted by sbauer1"AT"juno.com
Can I ask why your friend is anti-expansionist?! This seems to be an extreme position to take! Like deciding that you're not going to believe the earth is round, or deciding that all Moon landings were done in a TV studio!
In any case, I should attempt to explain the expansion of the Universe once more. The basic evidence is from measuring the redshifts of distant galaxies, and finding that the redshift increases with distance. This goes back to Hubble's original studies of 1926, so as you can imagine, we've come a long way since then! There is now no room for doubting that the redshifts of galaxies increase with distance from us. And the only viable interpretation is that the Universe as a whole is expanding, everything from everything else, so that *anyone* can consider themselves the centre if they like.
The CMB dipole shows that we *are* in fact travelling very fast through the Universe. Something like 600km/s for the motion of our Local Group of galaxies relative to the CMB photons. Remember also that on top of this, there is the motion of our Galaxy relative to the Local Group as a whole, the motion of the Sun round the Galaxy, and the annual motion of the Earth round the Sun - if you were to believe that we are genuinely at rest in a special place, then you'd have to decide which velocity is the right one!
I suspect that your friend may be confusing the expansion velocity with the small local velocity that each Galaxy has. You should picture the Universe as expanding smoothly in all directions. However, the individual objects in the Universe also have small gravitational effects on each other. So each Galaxy has a velocity on top of the Hubble expansion velocity, and this can be as much as several hundred km/s. This is just what you observe when you look at a cluster of galaxies - they have a whole bunch of velocities, with a spread of perhaps 500-1000km/s, but the average velocity of the cluster as a whole is the Hubble expansion velocity. This is just the same situation for our Galaxy - our local "peculiar velocity" is a few hundred km/s, while the Hubble velocity is zero here (as it is zero for all observers at their own location!).
The basic point is that the situation would be the same for an observer on any galaxy in the Universe: there is a relatively small peculiar velocity, on top of which the speeds of galaxies increase linearly with distance in all directions.
Results from the COBE satellite are one part of the clear picture we now have of how the Universe works. There are many articles you could read as background for the modern view of the Big Bang etc. I thoroughly recommend the article which appeared in Nature in 1992 (vol. 357, p288) by Peebles, Turner, Kron and Schramm or the similar one from Scientific American, which you can find here.
Expansion, as it is explained, occurs only in the voids of space,
namely the space between galaxies, not the galaxies themselves,
or the Earth, or my leg. So what's going on here? And given this
heterogeneous expansion, shouldn't there
be many directions (notably in the directions of galaxies and
large scale structure) where there will be a difference
in the CMB temperature due to travel time in areas of spacetime that
are not "expanding"?Submitted by sbauer1"AT"juno.com
The Universe as a whole is expanding, and this is a result of the large scale gravitational field of the whole Universe. However, on small scales, the gravitational effect of the Universe is easily overcome by the effects of any local concentration of matter. When our Galaxy (and other structures in the Universe) formed, the process started by having a local overdensity of matter (exactly where that came from is another story entirely!). This led to a little bit of gravitational attraction among the matter there, meaning that it was expanding a little bit slower than the Universe as a whole. Eventually the region became compact enough that it stopped expanding all together, started to collapse, and then complicated gas physics and other processes came into play and a galaxy was formed (again another story!).
This means that any object with a significant concentration of matter has locally stopped expanding with the Universe, although all the space between such objects is still expanding. Within our Galaxy the average density is around a million times the average density of the Universe, and so we are entirely dominated by "local" gravity. Hence all the objects within a galaxy, including the dust and gas clouds, the stars, the planets, the life forms, and their legs, are not expanding. But the vast amount of space in between the galaxies certainly is.
In fact there are effects on the isotropy of the CMB which come from just the sort of non-uniform expansion which you describe. However, those effects are certainly calculable - they turn out to be only important on very small angular scales, and even there they are always pretty much negligible. The reason is that if you are a photon crossing such a region, then you will blueshift on the way in and redshift on the way out, which almost cancels the effect of the local gravity. But there will be a small change in the energy of the photon due to any change in the gravity in the time it takes the photon to cross the object. This ends up being a much smaller effect than you might first have thought. So a smoothly expanding Universe containing no-longer-expanding objects (i.e. our Universe!) still has a very smooth CMB.
Does the CMB have a center or an edge? If so, where is the center and
edge?
Submitted by Pureman33"AT"aol.com
The CMB is just a uniform sea of photons, which are left over from the hot early phase of the Universe. So I'll assume that this question is essentially the same as asking about the properties of the Universe as a whole.
The simple answer is that the Universe has no centre, and no edge! And that the Universe doesn't have to be so simple that it's easy to get a clear mental picture of what's going on! In the theory of General Relativity (which as far as we know works very well for understanding gravity), space gets curved by the matter that's in it. So if there's enough stuff in the Universe, then space can be so curved that you could, in principle, set off in a straight line, go all the way "round" the Universe, and come back to where you started. Or alternatively if you could see clearly out to very large distances, you might be able to see the back of your head! If that was the case, then the Universe would be curved round on itself (in some abstract 4th dimension), so that it was finite in volume while having no edge.
On the other hand, most people's interpretation of the evidence is that there isn't enough mass to "close" the Universe. In that case, it is likely that the Universe is either genuinely infinite in extent, or at least so much bigger than the part we can observe, that it's infinite for all practical purposes. To understand that, you just have to realise that it's basically semantics: the Universe is everything, so it can't have an edge!
As far as a centre is concerned, the fact is that everyone is the centre! The whole Universe is expanding, everything from everything else, and so anyone can think of themselves as being the centre of the expansion. But in reality there is no special "centre" to the Universe. This obviously makes sense if the Universe has no edge, since it's clearly silly to think of the centre of something that's infinite.
So the best picture for the Universe is a very large (possibly infinite) thing, full of galaxies, which is expanding in every direction at once. The CMB is the background of radiation left over from when the Universe was very hot and dense. As the Universe expands it cools, and so we see the background radiation as microwaves, coming from all directions. There's no significant large scale pattern discernible on the microwave sky precisely because we live in a fairly mundane part of a Universe with no centre and no edge.
I study Physics at University and I am having trouble finding information on
things like: How are the initial density fluctuations related to the angular
fluctuations that we see in the CMB? And what would we observe if the
Universe were periodic?
Submitted by m.p.pendlebury"AT"ncl.ac.uk
If you are studying physics, then you ought to have enough background to read some of the original work in the field. You might like to start with the article in Annual Reviews of Astronomy & Astrophysics (1994) vol 32, p319, which you should be able to find in your University Library. That will give brief explanations of the questions you raised, and also point you to other relevant papers.
Of course much has changed in the last few years, but the basic physics remains the same, and this article in ARAA remains one of the best overviews of the subject (if I do say so myself!).
I am trying to get the CMB spectral data points for a plot and
data fitting routine which I will demonstrate in a graduate
thermodynamics course that I will start teaching soon. Could you
point me to a place where I can download the points, preferably with
attribution to each of the experiments?
Submitted by kevinmccann"AT"erols.com
It's always good to make your own plot, just to convince yourself that the CMB really is such a staggeringly good blackbody! There are rather a lot of different measurements now, so it's useful to have a place where you can look up a bunch of the data points. I think the best recent compilation is in George Smoot's conference review, which is obtainable at astro-ph/9705101
There's an explicit list of measurements at different frequencies, with error bars and attribution. There are also nice plots in our new web-update for the Particle Data Book (astro-ph/9711069), but we don't actually list the points there.
My question centers around the surface of last scattering. If I
understand correctly, some of the key equations that have been used to
determine the physics of the universe depend on two variables, one of
which has usually been ignored (the pressure?) because it becomes so
small as to be irrelevant. Does this assumption still hold at the time
of the surface of last scattering or should the pressure figure back
into the equations?
Submitted by rassler"AT"cleo.bc.edu
The pressure is certainly a very important part of the physics of what's going around redshift 1000 when the Universe becomes neutral and the photons last interact with the matter. So rest assured that when theorists calculate the real thing, they don't forget to include the pressure!
In today's Universe pressure on the whole is negligible. The Universe is dominated by regular stuff, which acts like a largely non-interacting fluid on big scales. Such stuff is usually referred to by the term "dust", which here has a technical meaning. So for the recent history of the Universe you can indeed ignore pressure.
But earlier in the Universe the radiation content becomes more and more important. And back when the Universe was so hot that all the matter was ionized, the photons were very strongly interacting with all those charged particles. At those early times in the history of the Universe, it would be a hopelessly bad approximation to neglect pressure effects. Indeed the effect of pressure on the generation of CMB anisotropies is very much tied up with the existence and detailed shape of the bumps and wiggles in the "power spectrum" of anisotropies, through which we hope to be able to understand all the physics of the large scale Universe!
What is the magnitude of our motion relative to the CMB (RA, Decl, km/s)?
Submitted by Wolverine"AT"netgate.net
The best number comes from analysis of data from the COBE satellite, and I will just quote those numbers. We are moving at a velocity of 370.6 +/- 0.4 km/s towards galactic coordinates (l,b)=(264.31+/-0.17,48.05+/-0.10). which corresponds to RA=11h12m, Dec=-7.2.
These numbers are specifically for the motion of the Sun relative to the CMB. Of course the Earth is in motion around the Sun, and so there is an annual variation in the Earth's motion relative to the background. In fact COBE was sensitive enough that it could detect the motion of the Earth by the changing temperature pattern in the sky throughout the year!
I'm writing a short paper for my undergraduate level introduction to
astrophysics course. The topic is on the source(s) of the CMB. What
are the most important physical processes that created the CMB photons?
It seems that baryogenesis, nucleosynthesis, and element formation are
all important, but I'm not sure where my focus should be.
Submitted by rkeyes"AT"rice.edu
The answer to this question depends to some extent on what you are really asking. In some sense the CMB photons that we detect were created in the Earth's atmosphere, as they are absorbed and re-emitted along the path of the light. But that's not a very useful answer! Along similar lines, the photons were last scattered at a few hundred thousand years after the Big Bang, and you can think of scattering as absorption of a photon and simultaneous emission of a new one in a random direction. As you go even earlier in the history of the Universe, individual photons interact ever more strongly with matter, and at times before about 1 year photons lose even energy information during scattering processes. So none of the photons we see today contain information about things happening before about the first year in the history of the Universe. What you presumably want to know is where the photons came from in the first place though!
The process of nucleosynthesis (formation of the light elements) happened in about the first three minutes. In fact there were already so many photons per baryon (normal matter particle), that the extra photons created from the nuclear energy released at this time are quite negligible.
At super-high energies particles and anti-particles were being created
and annihilated constantly -- appearing out of pure energy (photons) and
then annihilating again into pure energy. At higher energies even higher mass
particles and anti-particles were appearing and disappearing, and existed
in roughly equal numbers to the photons at that time. So early in
the history of the Universe there were lots of protons and anti-protons around,
for example, earlier than that there also lots of higher mass exotic particles,
and so on. The lightest particles we know about are the electrons, and so they
annihilated last. Before about 1 second the Universe was full of
electrons (e-) and anti-electrons (e+) and
photons (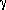
),
in about equal amounts. Then as the Universe expanded, the temperature
dropped low enough that if you annihilated an e+-e-
pair there wasn't enough energy in the average photon to recreate the pair.
So eventually the Universe lost most of its e+'s
and e-'s, and ended up with mostly 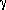's.
Why we have any e-'s left over is a good question
(that's baryogenesis), and I talked a little about that before.
But this annihilation process is basically what produced the photons in the
CMB, with most coming from e+-e- annihilation, some
contribution from
µ+-µ-
and 
+--
annihilation a little earlier and a tiny bit extra from nucleosynthesis.
And of course it's always possible that other unknown physical processes
occurring between the first 1 second and the first year could have
played some role in generating extra photons as well.
I'm doing an essay on "Penzias & Wilson and the discovery of CMB". I
would be very grateful if you could send me any information on the
discovery of CMB and on Penzias and Wilson themselves.
Submitted by ketal.patel"AT"ic.ac.uk
This story has been told many times before, and by people much better qualified than me to tell it, who also did a much better job than I could do here! So let me just suggest places where you can read more about the history of the discovery. One excellent place to start is the popular book "Afterglow of Creation" by Marcus Chown (University Science Books). This gives an excellent overview of the whole story, written in an exciting way, while being pretty fair on all the main players, and presented at an accessible level. This is a book I'd recommend to my mother!
For more "on the spot" viewpoints, which are necessarily more subjective, you can't do better than the articles written by Wilson himself, although they may be a little hard to obtain (in Physica Scripta, vol. 21, p599 (1980), and in the books "Modern Cosmology in Retrospect", edited by Bertotti et al. (1990), and "The Cosmic Microwave Background: 25 Years Later", edited by Mandolesi & Vittorio (1990)). The Princeton point of view is presented in Peebles book "Principles of Physical Cosmology" (1993), as well as in an article by Wilkinson & Peebles in "Serendipitous Discoveries in Radio Astronomy", edited by Kellermann & Sheets (1983).
There are even more intriguing parts of the story involving "predictions" of the CMB by Gamov and collaborators (see Alpher & Herman's article in Physics Today, August 1988 issue) and regarding whether the CMB had already been inadvertently detected, either through anomalous excitation in interstellar molecules by McKellar as early as 1941 (see Thaddeus in Annual Reviews of Astronomy & Astrophysics, 1972 for more details), or in radiometer measurements by Ohm and others in the early 1960s. There is a fairly extensive discussion of these topics in the review article (in english) by Melchiorri & Melchiorri in La Rivista del Nuovo Cimento, vol. 17, no. 1 (1994), as well as the book "3K: The Cosmic Background Radiation" by Partridge (Cambridge, 1996).
I am wondering what the redshift is to the last scattering surface.
Also, shouldn't
this give a very good number for the age of the universe? That is,
aren't the
theories about the temperature of the universe at last-scattering times
very good,
and so shouldn't the observed redshift of the CMB give a very tight
estimate? What
am I missing?
Submitted by billgr"AT"sunoptics.caltech.edu
Let me review the nature of redshift first.
Since more distant things have their light more shifted towards the
red end of the spectrum, then we can use this "red-shift", conventionally
denoted by z, as a measure of
how far away something is. Light takes longer to get to us from more
distant objects, and so when we see something at high redshift, we are
seeing it as it was when the Universe was much younger; hence redshift is
also a measure of time back into the early history of the Universe.
In the standard expanding Universe models, it is best to think of redshift
as being due to expansion rather than velocity. In other words, if you see
something shifted towards the red, that's because the light was emitted when
the Universe was smaller, and as the light travelled towards you it expanded
along with the rest of the Universe, having longer wavelength by the time
it reached you. So objects seen in the more and more distant past are
seen with their light redshifted more and more (because the Universe is
smaller and smaller as we approach t=0).
Redshift zero is today, the most distant galaxies are seen at about
z=5, the CMB photons last scattered at approximately z=1000,
and the Big Bang took place at z=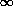
.
What exactly was the redshift of last scattering of CMB photons? Well, the last scattering surface is really a shell rather than a surface, ie there's a range of redshifts over which the photons suffered their last interaction with matter. The central redshift is around 1100, with a width of about 100 in z. This depends a little bit on the precise cosmological model (eg how dense the Universe is, or how fast it is expanding), but surprisingly doesn't change very much. It's a pretty good approximation to look at some CMB photon that you've just detected and say "this photon probably last interacted with matter back at z=1100". (What age the Universe was at that redshift does of course depend a lot on the cosmological model, which is precisely why cosmologists use redshift as their measure of time!).
The second part of the question above concerns predicting the CMB temperature. It's true that there are some rough arguments for the order of magnitude of the CMB temperature. But there is no precise prediction for how hot the radiation background should be. What I know is that if the temperature is about T0=2.73K today, then the photons last scattered at about z=1100 (when the matter was going from an ionized to neutral state). If I measured a different temperature for the CMB today, then I'd infer a different redshift for last scattering. Say for example that T0=10K instead, then I'd infer that I lived in a Universe where there was more radiation, and the last scattering redshift would have been substantially lower.
It would be great if there was an independent method to predict the redshift
of last scattering, since then I could indeed use the measured CMB
temperature today to constrain the age of the Universe at the last scattering
time. Unfortunately no such independent estimates exist, and so I can
only tell you that last scattering is at z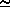
1100
because I've measured T0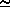2.73.
What are the significant factors that the CMB has contributed to developing
our cosmological ideas? (apart from being a large constituent
of the proof of the Big Bang).
Submitted by micky"AT"acon.com.au
So being a cornerstone of the Big Bang isn't enough for you, eh?
To summarise how important it is in this regard: the discovery and confirmation of the CMB was instrumental in building our current picture for how the whole Universe behaves with time. Namely, that it used to be very much hotter and denser, and is continuing to expand and cool.
But there is more to it than that. The precise black-body (thermal equilibrium) nature of the CMB spectrum has ruled out any other serious possibility for modelling the evolution of the Universe. Moreover, it puts precise limits on a wide range of physical processes occurring over timescales of roughly 1 year to 1 million years after the Big Bang (since these would lead to "distortions" in the spectrum, which are not seen).
Separate from that are the basic things that the CMB spatial patterns tell us. Basically, the near isotropy of the temperature is very strong evidence that we live in a Universe which is very smooth and uniform on large scales. So our Universe is pretty much the same in every direction, doesn't rotate much, etc.
The the detection of tiny differences in temperature on the CMB sky tells us about density fluctuations on large scales in the early Universe. Here we are learning a lot very rapidly, so the picture is still not entirely clear. For sure we have learned that gravity alone is probably responsible for growing all of the structures in the Universe. Secondly, it appears that there are fluctuations on the largest scales, of just the kind that so-called "inflationary" models of the early Universe predict. How far that goes towards proving inflation is still a contentious question though!
Certainly we now know the amplitude and shape of the "initial conditions"
for density fluctuations in the early Universe. We also know that general
models with a large component of Cold Dark Matter look like they're on the
right track. And in the near future we're going to start learning more
details about the values of fundamental cosmological parameters, like
0, so we can tackle questions such
as "will the Universe expand forever?", "how old is it?", "how much
stuff is there?", "where did it all come from?", etc.
Can you postulate any other plausible explanations for the 2.73K CMB
temperature other than residual radiation from the Big-Bang? Couldn't
heat radiated by our galaxy itself into a surrounding cloud of
intergalactic dust or hydrogen be the reason for the CMB?
Submitted by stardot"AT"worldnet.att.net
The assumption that the microwave radiation we observe is a remnant of a hot phase in the early universe is obviously a fairly radical one. And so we have to make sure that we have exhausted all reasonable options before deciding this is the best explanation. Because this is quite an important question, my answer will be somewhat involved.
Hot gas tends to emit or absorb in various spectral lines or bands. Dust being zapped by starlight or other radiation will cool by emitting a fairly continuous spectrum. However that spectrum tends to be characteristic of temperatures somewhat higher than 2.73 Kelvin. Typically cool clouds in the interstellar medium of our galaxy are maybe 100K, with some rare cases as low as 10K. But it is generally only the very densest cloud cores that have temperatures as low as even 10K. Although the spectrum from radiating dust grains is fairly smooth, it is generally not well represented by the standard "blackbody" shape, but varies somewhat differently with wavelength (technically modelled with an "emissivity index" which would be zero for a blackbody, but is usually between 1 and 2 for interstellar dust). There are also broad spectral features in the spectra of dust grains, which would be seen as deviations from a blackbody shape.
When the spectrum of the CMB was still rather crudely determined, it was still possible to contrive models where there was very extended dust which was absorbing starlight and re-radiating it as microwave radiation. But as the spectral measurements became more and more precise, such models got backed further and further into a corner. The last remaining notion held that perhaps grains of a special shape and composition (so called "iron whiskers") might fill the Universe and give radiation more or less indistinguishable from a blackbody. However, the exquisitely accurate blackbody shape measured by the FIRAS experiment on the COBE satellite killed even this idea. Now there is no type of dust that we can think of that would be able to fit the spectral shape which has now been measured so precisely.
On top of that, any dust would have to be extremely uniformly distributed in order not to give itself away in the spatial fluctuations on the sky. Recall that the fluctuations in the CMB temperature in different directions on the sky are about one part in 100,000 of the overall temperature. If the emitting material had anything to do with our Galaxy, then it would be expected to vary on the sky in a way which correlates with the plane of our Galaxy. No such variation is seen in the 2.73K CMB emission.
A further constraint is just to ask what other effects such dust might have. If you have enough dust around to emit that much microwave radiation, distributed in our Galaxy and presumably every other galaxy, as well perhaps in intergalactic space, then it turns out that it would have a very significant obscuring effect on distant galaxies. The fact that we see distant galaxies and quasars in every direction we look, except right through the plane of our Galaxy (where we know our view is blocked by thick dust), implies that there isn't obscuring dust all over the place in the Universe. Working through the numbers makes it very hard to have enough dust to radiate significantly at microwave wavelengths, without blocking our view of distant objects.
One last piece in this puzzle is that in fact the general emission from dust emission has been seen and that it peaks around 200 microns (or 0.2mm) in wavelength. This is almost a factor of ten shorter wavelength than where the CMB peaks, and the total energy in this "far-infrared background" (FIB?) is about 30 times lower. There is good reason to believe that this background is due to the emission from dust in galaxies distributed throughout the Universe, with the dominant contribution coming from galaxies which are undergoing periods of rapid star formation. So the cosmic emission from dust has been discovered, and it is something very different from the CMB (and of course interesting in its own right).
Somewhere I've seen the CMBR temperature stated as 2.728K; elsewhere as 2.726K.
Could you give us an idea of the latest estimates, with references? Just how
dependent is this calculated temperature upon the value of k, the Boltzmann
constant, only known to something like 8.5ppm? Is the CMBR
energy value currently more precise/accurate than the CMBR temperature value?
If so what is the value in energy units of your choice?
Submitted by jebush"AT"ridgecrest.ca.us
The best temperature for the CMB is currently 2.728+/-0.004K, where this uncertainty represents a statistical 95% confidence region. This comes entirely from analysis of data from the FIRAS experiment on the COBE satellite. The reference is D.J. Fixsen et al., Astrophysical Journal, Vol. 473, p. 576 (1996), if you are interested. So far there is little extra limitation on the temperature from the other experiments, which operated over a wider range of wavelengths but with much less precision. This situation will obviously (one assumes!) change with time as more precise data become available.
Boltzmann's constant k is what you multiply temperature by to get an energy. As has been pointed out, k is not known to infinite precision, but is 1.380658(12)× 1023J/K, where the number in brackets indicates the uncertainty in the last 2 digits. However, this constant is known much more accurately than required for getting at the CMB temperature. I suspect I will not live long enough to see uncertainties in fundamental constants being the limiting factor on getting a precise CMB temperature!
The useful quantity for the CMB is the amount of energy per unit volume, or the energy density. As to whether this energy density is better known than the temperature, I'm not entirely sure. There are probably several places that things like the Boltzmann constant enter indirectly (certainly in the calibration process I should think), which will confuse matters. But rest assured that at the moment our knowledge of the energy density, the number density of photons and all similar quantities is just limited by uncertainty in the temperature. For your information: there are about 412 CMB photons per cubic cm (with an uncertainty of about 1); the energy density is the equivalent of 0.261 electron Volts per cubic cm (again uncertain by about +/-1 in the last decimal place); the equivalent mass density is 4.66 × 10-31 kilogrammes per cubic metre; the peak of the spectrum is at a frequency of 160.4 GHz (uncertain by about +/-0.1); and the peak intensity of the background is about 385 MJy/Sr (that's MegaJanskys per Steradian, which is not a unit you meet everyday!). I hope that's enough numbers for you!
In your answer to the "How come we can tell what motion we have with respect
to the CMB?" question, there is one more point that could be mentioned.
In an expanding universe, two distant objects
that are each at rest with respect to the CMB will typically
be in motion relative to each other, right?
Submitted by fklaess"AT"pt.lu 10/98
The expansion of the Universe is certainly an inconvenience when it comes to thinking of simple pictures of how things work cosmologically! Normally we get around this by imagining a set of observers who are all expanding from each other uniformly, i.e. they have no "peculiar motions", only the "Hubble expansion" (which is directly related to their distance apart). These observers then define an expanding reference frame. There are many different such frames, all moving with some constant speed relative to each other. But one of them can be picked out explicitly as the one with no CMB dipole pattern on the sky. And that's the absolute (expanding) rest frame!
I'm looking at the physical properties of blackbodies. The graph
shows the max of the CMB curve at about 2mm.
The Wien displacement law claims T = k/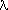
,
so T(Kelvin) 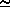2.9/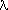(mm).
Therefore the CMB Temperature is 1.4 Kelvin. What's the trick here?
Submitted by GASNER"AT"aol.com 10/98
A hot object emits energy over a range of wavelengths. Ideal hot objects
are called "blackbodies".
Wien's law is the simple property of a blackbody, which says that the
peak output (in wavelength) is related to the temperature: hotter objects
peak at shorter (bluer) wavelengths, cooler objects peak at longer (redder)
wavelengths. The usual formula is that
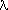peak×T=2.9. What Wien's law tells you
explicitly is where the energy emitted per unit time per unit area
per unit wavelength peaks. This quantity is usually called "intensity".
When you deal with intensity you are free decide whether you want to use
wavelength units or frequency units (since they are just related by the
speed of light: ×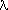
=c). For
wavelength units the natural thing is to deal with
I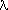, the amount per unit wavelength. If
you are using frequency units (Hz), then it's natural to deal with is
I, the quantity per unit frequency.
The peak for I is shifted a bit compared to
the peak for I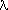. Knowing the shape of
one curve you can easily work out the shape of the other. So it's
straightforward (if a little messy!) to work out the shift. Take my word for
it that the peak of the I is at
a frequency corresponding to the wavelength for which
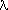peak(mm)×T(K)=5.1.
For this curve the blackbody peak for the CMB is at about 2mm, and so this
must have been what you saw plotted. For an
I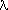 plot, the peak would be more like
1mm.
Several years ago on some television show
(probably PBS, NOVA) they did a piece on background radiation, with an
interesting twist. The scientists involved converted the
radiation they were detecting into humanly audible wavelengths of
sound. This was an incredibly fascinating noise, besides being the
"sound of the universe" it came across as a mix of white noise and
hypnotic repetition.
I was hoping there would be someone on the internet
broadcasting this converted sound, but no luck
so far. If you know what I am talking about and have any recordings of
background radiation lying around (or know where I could be directed),
I would greatly appreciate it.
Submitted by michael_wynne"AT"yahoo.com 10/98
I dimly recall such a thing too. Anyone else remember the specifics? Let me know!
The frequencies are many orders of magnitude higher than anything that you could hear. On the other hand the wavelengths of the photons in the CMB are quite similar to the wavelengths of sound that you can hear. So if you took the waves to be sound waves and generated a range of waves with intensities given by the shape of the blackbody spectrum of temperature 2.7 Kelvin, then I guess that that would be like "hearing the sound of the Universe". Sounds like a cool idea!
The result would sound like "noise", although there would be a range of wavelengths, peaking at some particular value (roughly 1mm), so I'm not sure exactly how that would sound. Certainly it would be repetitive! I think in fact the wavelengths are a little short, so you may have to cheat by a factor of maybe 100 in order to get it near the centre of your ear's response. I suspect also that, because the ear is a kind of logarithmic detector, you might have to play with the intensity scale too in order to hear something interesting.
Could you tell me specifically what is the wavelength and frequency of the
CMB?
What is the irradiance in watts per square meter of the CMB at the surface
of the Earth.
Is there a receiver design/circuit published that one could build to detect
and monitor fluctuations in the CBR.
Submitted by amchitka"AT"email.msn.com 11/98
The CMB has a "blackbody" spectrum, i.e. its spectrum covers a range of wavelengths (or frequencies), peaking at around a couple of millimetres (or a frequency of around 150 GHz). This peak, and the general shape of the spectrum is characteristic of the emission from something (in this case the whole Universe!) which is in thermal equilibrium at around 3 Kelvin. You can calculate the flux from summing up the contribution from the blackbody spectrum. The answer is that there are about 400 CMB photons in every cubic centimeter of the Universe, all moving at the speed of light, and representing a flux of 3.14× 10-6W/m2 (at the surface of the Earth, and everywhere else!).
Detecting the CMB itself is relatively straightforward, since you can't help detecting it in any broadband receiver which is sensitive anywhere in the range from a few GHz to a few 100 GHz. However, it doesn't seem particularly exciting, since it's basically just excess noise. Basically the CMB just adds to the background hiss, but it's the the level of background which you can't get rid of by designing a more careful receiver (this is just how Penzias & Wilson detected it back in 1965. So the answer is that it's fairly easy to detect the CMB, but probably fairly hard to convince yourself you've detected it!
The fluctuations are another matter though, since they are always going to be very hard to detect. The dipole (one side of the sky hotter than the other) is 100 times harder to see than the CMB itself. I suppose this might be feasible with home-made equipment. You'd need to look for the difference in the "noise" between a couple of well-separated directions (and avoiding the Galactic plane, which tends to get in the way). Smaller scale fluctuations are about 1000 times fainter still, and are hard even for the best experiments in the world!
I have been thinking about the prediction
of the CMB temperature in the 1940s.
Is it possible to predict the CMB temperature knowing only the
Hubble constant and the ratio of neutrons to protons or do you need
some extra assumptions?
Submitted by schleif"AT"mail.desy.de 11/98
In a number of papers in the late 1940s and early 1950s Alpher, Herman & Gamov predicted that there might be a thermal background from a hot early phase in the Universe. There are many variants on the way the argument goes, but let me try to simplify.
The basic idea is that you want to start with a Universe which is an equilibrium of high energy particles (including photons), and then build up the light elements as the Universe expands and cools. To get a Universe which contains a reasonable amount of helium as well as hydrogen (all observations suggest that the average parts of the Universe have about 25% helium by weight) you need to have nuclear-type temperatures when the age of the Universe was about the time it takes a free neutron to decay. In rough numbers you want the Universe to be filled with billion Kelvin radiation when it was a few minutes old. If you also have a rough idea for how fast the Universe is expanding today (the Hubble constant), then you know approximately how old the Universe is today, and how much it has expanded since it was a few minutes old. Then you can estimate the current temperature of the radiation that was a billion Kelvin at those early times, and you get a number which comes out maybe around a few Kelvin today.
This is not an accurate prediction. It just says that you shouldn't be surprised to find relic radiation with a temperature of a few Kelvin today. You can probably refine this to give a decent guess for the CMB temperature within a factor of 3 or so. But there are too many uncertainties to get it much better than that. Really the CMB temperature is a quantity which should be measured in order to constrain other things within cosmology.
The field of "Big Bang Nucleosynthesis" is essentially the opposite of this argument. You take all the estimated primordial abundances of light elements (the isotopes of hydrogen and helium, together with lithium, and perhaps traces of beryllium and boron) and find that you can fit all the data if you have a single value of a particular parameter. This parameter is the ratio of the density of photons to baryons today (baryons are protons plus neutrons). So if you know the temperature of the CMB, and hence its density, you can use these light element abundances to estimate the density of baryons in the Universe. It's the fact that this comes out about a factor of 10 less than the total amount of mass inferred to be in the Universe, that leads us to believe that there's lots of "dark matter" out there.
Gamov, Alpher & Herman's old argument is basically a crude version of these nucleosynthesis calculations, where you assume some value for the baryon density today, and hence predict the photon temperature.
Is the CMB simply high energy photons that originated at
the origin of the universe that have been red-shifted all the way to the other
end of the electromagnetic spectrum because of the expansion of
the universe? Or is it something more complicated than that?
Submitted by bchaikin"AT"aol.com 11/98
You've got it!
Let me qualify that by saying that the CMB photons were made long after the origin of the Universe (whatever that was). Here by "long after" I mean maybe seconds!
The CMB derives from a time when the Universe was so hot that a whole bunch of particles were being created and annihilated rapidly, and so were in equilibrium with the photons. There were essentially equal numbers of all the particles you've ever heard of, including photons. As the Universe expanded and cooled various particles annihilated (there wasn't enough energy around to recreate the particle-antiparticle pairs once they had annihilated to photons), increasing the number of photons relative to matter particles. At this point the CMB photons were really CGRB photons, since they were high energy gamma-rays. The last such event (electron positron annihilation) was about a minute after the Big Bang. So the photons weren't really made in that first instant, but a lot later!
These photons stretched in wavelength along with the expanding Universe, as you rightly say. But they were still exchanging energy with the matter, and in fact there were processes which could generate new photons right up until about a year after the Big Bang. At that point the photons were low energy X-ray photons. After that, there were still slow processes that could affect some of the photons (changing their direction or mildly changing their energy), and they only really stopped interacting with the matter when the Universe became neutral around 300,000 years after the Big Bang. At that point the photons were in the near-infrared part of the spectrum. Since then they've interacted almost not at all, and have travelled through the expanding Universe being redshifted into the microwave region.
I'm a skeptic who frequently encounters arguments for the existence of
god from Christians utilizing CMB. What puzzles me is that, although
they accept CMB as a "fact," they ignore the part about the universe
being 10-20 billion years old.
Is a 10-20 billion year old universe an essential element of the modern
astronomical theory of the big bang and CMB? Or would the theory work
just as well if the universe is only a few thousands years old?
Submitted by xfaberman"AT"sprynet.com 2/99
This may be a difficult question to answer, since I usually try to avoid treading on people's religious opinions. However, there is a big difference between a reasoned set of beliefs in a spiritual entity, and some craziness which invokes half-understood scientific concepts in order to bolster some wacky theology!
My understanding is that there is no such thing as a proof of the existence of God. And that indeed such a proof goes against a basic principle of many of the world's major religions, where to have Faith is something which transcends the idea of scientific proof. But then I'm no theologian, so perhaps I'm entirely wrong here.
What I do understand is some scientifically consistent picture of how the Universe behaves. So let me stick to that, and leave all questions of how that may (or may not) relate to particular religious viewpoints to each individual to sort out for themselves. It seems like that a physical reality exists, and that it can be understood by applying the principles of rational thought and empirical testing. This is the Universe I know and love, and I have a pretty coherent picture for how the CMB fits into it!
When the CMB was first discovered, and for several years after that, it was not clear exactly what the origin was. The "remnant of the Big Bang" idea made the most sense, but for a while the possibility existed that the CMB could be produced locally, by emission from some sort of dust grains, either in the vicinity of the Sun, or perhaps distributed through the local Universe. As the spectrum was measured to be closer and closer to "blackbody", such alternative origins of the CMB became less tenable. And there are other arguments against such ideas, e.g. how come we can see very distant galaxies through all this supposed dust? So now we firmly believe that the only reasonable explanation from the CMB is that it is the radiation left over from a very hot early phase of the Universe.
There's no way to reconcile the CMB with a Universe that is very young (unless of course you just make the Universe look like it's old!) But then you can't reconcile a several thousand year old Universe with any number of other observations either: historical records and archaeological evidence that human civilization was around many thousands of years ago; everything we know about geology, e.g. the ages of various rocks on Earth, the Moon, meteorites etc.; observations of astronomical objects which are much further than a few thousand light years from us; etc. etc.
To me, the cosmic background radiation (alone) merely suggests
some past or current universal substance or phenomenon which is both
highly isotropic and highly opaque.
I am very curious as to the strict limits
current CBR evidence places on "Hat-stand" cosmological speculation. For
example, does the CBR, by itself, effectively rule out flat space? A
periodic universe? A trillion year old universe? A vast universe?
Submitted by hazelf"AT"ix.netcom.com 2/99
You are right in essence, that the CMB by itself suggests "some past or current universal substance or phenomenon which is both highly isotropic and highly opaque". But of course it can't be taken on its own, since there are many other well-established facts that we now know about the Universe. For example, we have known for almost 75 years that the universe is expanding. Together with the CMB, this implies that there was an earlier, hotter, denser phase in the history of the Universe, and that the CMB is the relic of this phase. I know of no reasonable alternative.
As for whether the CMB rules out various "hat-stand" ideas, it depends how crazy they are! Certainly there is an ongoing investigation into the curvature of the Universe as a whole, and within some bounds we are currently unsure about how curved it is. The best solution currently is flat (but expanding) space, with some amount of vacuum energy density (also called a "cosmological constant") contributing. But it could have negative curvature (an "open" universe), and the closed geometry isn't entirely ruled out either (although currently not favoured).
The space-time structure of the Universe could also be periodic in some way, but only if the scale of the periodicity is very large, otherwise you mess up the CMB in a big way.
The question of how old the Universe might be is an interesting one. There are lower bounds on the age of the Universe by finding the oldest things in it (e.g. globular clusters). But it's less clear how you might get an upper bound. The best-fitting versions of big bang models expand from a time around 13 billion years ago, and they don't work too well older than say 15 billion years (assuming nothing particularly funny happens). But I'm sure you can't currently rule out a universe that did basically nothing for a trillion years and then decided to expand rapidly, or one that might have had a previously contracting (or even expanding) phase, or indeed many phases before that. To some extent we then get into metaphysics, since it's not obvious that you could ever test such a hypothesis. Still, the simplest solution is that our current phase is the only one there's been, and that it can't be a trillion years old.
My view is that the CMB, together with the wealth of other information we have about the Universe as a whole, paints a pretty coherent picture. And this picture - that the Universe began around 15 billion years ago and has been expanding and cooling ever since - sounds crazy enough! The reason it is believed is that it is a very simple idea, and that it works astonishingly well.
If the CMB was created by the Big Bang and the proceeding few moments of the
early universe, then shouldn't it have had plenty of time to whizz off into
outer space, way faster than the non-light-speed matter (e.g. us) have been
moving out from the Big Bang site, in which case we shouldn't be able to
observe it, I'd have thought?
Submitted by vince.bowdren"AT"jobstream.co.uk 3/99
This is similar to other question which I have received many times. The answer is very simple - your mental picture is incorrect! Since the Big Bang model, the expanding Universe, the speed of light etc., are all far from everyday experience, there are many ways in which people can get the wrong image in their heads.
The first thing to get straight is that there's nothing outside the Universe! By definition the Universe is everything there is: we live inside it; and it isn't expanding into anything.
The next thing you have to get clear is that the Big Bang happened everywhere at once, and shortly afterwards all of the CMB photons were created and suffered their last interactions with matter. So those photons are indeed shooting off into space in all directions at the speed of light.
The CMB photons we see today are coming to us from way across the Universe (about 13 billion light years away, if for example the Universe is 13 billion years old). That's true no matter what direction in the sky we look.
It might help to think what happened to the photons that were made right here, all that time ago. Those particular CMB photons have been whizzing off at the speed of light in all directions, and are now being detected by distant observers (say 13 billion light years away) as part of their Cosmic Microwave Background.
I'm an undergraduate student who is taking an Astronomy course
(abridged) ... can you check these CMBR questions for my last assignment?
Submitted by mmar"AT"sprynet.com 3/99
Q: Explain why the cosmic microwave backround is considered good
evidence for the big bang theory?
A: Cosmic microwave background radiation is found everywhere,
filling all
space. It had been predicted in 1948 by George Gamow's collaborators as
the cooled remnant of the hot fireball created in the Big Bang. The
Universe therefore appears to be changing with time. This conclusion is
supported by the observed evolution of galaxies and quasars as we look to
distant and therefore younger reaches of the Universe. We therefore
exclude the Perfect Cosmological Principle and the Steady State theory, and
accept the Cosmological Principle and the Big Band as basic premises. The
2.73K CMB is residual radiation left over from the Big Bang.
Q: Why is the cosmic backround such a low temperature today?
A:
The stretching of wavelength with expansion
can account for its lower temperature.
Photons do not slow down. Only wavelengths and
frequencies are affected by the expansion. Redshifting what would have
been on average visible light photons to that of microwave region by the
continued expansion of the universe is the important effect.
Pretty good answers I'd say, which I only edited a little. Pity it was too late to help you with the assignment! Did you pass I wonder?
What physics would fractal analysis of the CMB reveal or constrain, if
any?
Submitted by tr211"AT"hermes.cam.ac.uk 4/99
The short answer is none!
The slightly longer answer is that, to the extent that the fluctuations in the CMB behave approximately like a power-law in scale, at least at the largest angular separations, then this analysis has already been done extensively for the COBE data. Whether or not people referred to it as a fractal is a matter of personal preference, but you can certainly read all about these analyses in the original papers in the Astrophysical Journal. However, there's now pretty good evidence that this power law (or fractal) behaviour doesn't continue to smaller scales. Moreover, the simplest theories predict excess fluctuations on degree scales, and a rich structure at scales below that. Far more interesting and informative than a boring old fractal!
Assuming the universe to be fourteen billion years old - how much energy
(in ergs) would the CMB contain (in the universe)?
Submitted by sclufer"AT"pop.erols.com 6/99
Since we know the temperature of the CMB quite accurately, and we know that it is very well described as equilibrium (blackbody) radiation, then we know pretty much everything about it. In particular it's energy density is just a standard physical constant times the temperature to the fourth power, which comes out to be about 0.262 eV cm-3, or about 4.21 × 10-13 ergs cm-3. (I could ask why you are using an antiquated unit like the erg, but let's not quibble!).
There's always a problem with what you mean by "the Universe", since in principle it could be infinite. However, in practice, we only know about the region that light can have reached us from in the age of the Universe. If the Universe is 14 billion years old, then the observable universe is about 14 billion light years in radius (actually a little different from this, since it's been expanding, but we've already agreed not to quibble!).
So the total energy of the CMB in the observable Universe is just the energy density multiplied by the volume of a sphere with radius 14 billion light years. This turns out to be about 4 × 1072 ergs. In whatever units you use, that's a lot of energy!
Assuming the critical density is 5 × 10-30 g/cm3
(about equal to
one hydrogen atom in a container 130 centimeters on a side averaged
averaged over the entire observable universe),
how many ergs are we talking about? How does this compare with the CMB?
Submitted by sclufer"AT"pop.erols.com 7/99
What you want to compare is the energy equivalent of that mass density. So you multiply the mass density by c2 to get energy density (using the famous equation!). What you'll find is that the CMB energy density is about 10,000 times smaller than the current mass density. The precise value depends on: (a) how much dark matter there is; and (b) how fast the Universe is expanding.
In more detail, the critical density is given by the formula
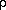critical=3 H02/(8 
G),
and the actual density is a factor of times that
(where lies between 0 and 1 in all likelihood, and
tells us what fraction of this critical density the observed Universe has).
If you write the Hubble constant as
H0=100×h km/s/Mpc, with "h" parameterising our uncertainty in
the Hubble constant (probably 0.5 < h < 0.8),
then the density of the Universe is
a numerical factor times h2.
You can then multiply by the speed of
light squared to get the equivalent energy density. Then taking
the ratio of this with the energy density of the CMB, gives you a value like
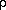matter/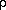radiation = 40,000 h2.
For all reasonable values of and h this lies close
to 10,000.
Because this number is so big, we talk about the Universe today being
"matter dominated". However, we know that when you squeeze a box full of
radiation and matter this ratio goes down. So in the expanding Universe we
expect that if we go back early enough it is the radiation energy density
which dominates. Hence we talk about the early Universe
(before about 100,000 years after the Big Bang) being "radiation dominated".
When light travels through a gravitational field it bends and can
also redshift. When light travels for 40 billion years through space and
gravitational fields it must redshift. Is this taken into account when
considering the Hubble constant and the age of the universe?
Submitted by DNoga"AT"stpaulshosp.bc.ca 8/99
The short answer is "yes", and I'm tempted to just leave it at that!
But habit forces me to be more long-winded.
First let's make clear that estimates for the age of the Universe come in around 14 billion years (40 is way on the long side). These estimates involve figuring out the age of the oldest things (e.g. globular clusters) and also determining how fast the Universe is expanding together with how much the expansion rate has been changing. Explicit calculations are done in the context of models of simple space-times which are consistent with Einstein's General Theory of Relativity, and thus properly contain all the effects of gravitational fields.
It may also help to clarify the redshifting effect. The effects of gravity are usually described by the "gravitational potential". In empty space this potential is unchanging, and you can think of a clump of matter as being a "potential well", i.e. a region where the potential is lower (actually the sign of the effect is really unimportant, but the convention is to think of matter as "holes" in the potential). When light leaves an object at the bottom of a potential well it gets gravitationally redshifted on its way out. Hence light coming from the surface of a white dwarf or neutron star (which are quite deep potential wells) can be significantly redshifted, and light from near a black hole would be hugely redshifted. Similarly, if you lived inside a potential well, then you'd see all the light from outside being blueshifted. BUT light that travels straight through a potential well gets blueshifted on its way in, and redshifted on its way out, by an amount that cancels. So you get no effect.
In detail, the bending of light and redshifting around clumps of mass in the Universe can have exciting observational consequences. All of the rich phenomena of gravitational lenses for example. There's also direct relevance for the CMB, because on small scales the CMB photons get affected by clumps of matter in the relatively nearby Universe, creating small-scale hot and cold spots ("anisotropies") on the CMB sky. Gravitational lensing affects the CMB anisotropies at levels which are measurable. And another possible signal comes from the effects of potential wells which were changing during the time the CMB photons crossed them. These give very weak effects which may one day be detectable on the angular scale of galaxies or clusters of galaxies, perhaps giving us more information about how such objects formed.
Has the redshift of a practically ideal blackbody like the CMB actually been
measured or calculated from a model? If measured what absorption line was
used as a reference?
Submitted by LABELE"AT"aol.com 9/99
It sounds like you have already answered that question! Since there is no reference line, you can't measure the redshift. In fact there's no way to tell the difference between a blackbody at lower temperature and a blackbody which has been redshifted - the spectrum retains exactly the same shape as the Universe expands. If you think about it, if that were not the case, then the CMB spectrum would change shape as the Universe expanded, and hence it would be pretty unlikely that we'd observe it to be such a precise blackbody shape today.
To put it another way, you can think of the CMB as being roughly 3 Kelvin blackbody radiation existing today, or as 30 Kelvin blackbody radiation which has been redshifted by a factor of 10, or as 300 Kelvin radiation which has been redshifted by a factor of 100, etc. They are all equivalent.
As far as the theoretical picture is concerned, the CMB photons last interacted with matter when the temperature of the Universe was about 3000 Kelvin, and the photons have redshifted about a factor of 1000 since then. So you can think of them as being a view from that redshift. But the photons themselves were produced much earlier, in a much hotter phase. And so it's probably best to picture them as the glow from period in the early Universe when the temperature was billions of Kelvin, and since the Universe has expanded by factors billions since then, we observe the CMB today at 3K.
Although there are general arguments (involving synthesis of the light elements in the early Universe for example) for predicting that the CMB should have roughly the order of magnitude of temperature that's observed (and these arguments were discussed as early as the 1940s), I've no doubt other arguments would be put forward if it had turned out to be a quite different temperature. There's no fundamental reason known which can explain why the current temperature is 3K rather than, say, 5K or 0.2K.
Does the time of decoupling have anything to do with the
mean free path of photons when the universe expanded and cooled to
approximately 3000 K?
Submitted by LABELE"AT"aol.com 9/99
Yes!
At around 3000K the radiation was cool enough to allow the electrons to combine with the nuclei (mainly hydrogen and helium), and so the Universe became neutral.
Now photons interact much more strongly with charged particles than they do with neutral ones (not surprising, since photons are the carrier particles for the electromagnetic force). In particular, interactions with free electrons were frequent when the Universe was ionized. But once the Universe became neutral (when the temperature dropped below about 3000K) the photons no longer "saw" the matter, and just travelled freely through space. The average distance between photon encounters with matter (otherwise known as the "mean free path") went from being very short, at earlier times, to extremely long at later times. The era that marks this change is the "last scattering epoch" when the Universe became neutral.
We see the CMB anisotropiesfrom mainly around this time - it's impossible to see much further back than that, since it's like looking through a dense fog. The CMB sky can be thought of as a distant sphere surrounding us, with the anisotropies that we see being places on that sphere where the "fog" was a little thicker or a little less thick.
I was wondering why CBR is reaching us only now; was the initial
expansion of the universe at such a great
rate the light could not match its pace and is hence reaching us only now?
Submitted by hbchai"AT"hotmail.com 10/99
As I have said when answering similar questions before, I think you need to get a better mental picture of the CMB, in order not to confuse yourself. For this purpose it's much better to think of ourselves at the centre of a spherical region of the Universe, with CMB photons coming at us from all directions (people at other locations in the Universe can also think of themselves at the centre of a spherical region, so there is no implication of a true centre of the Universe!). We will see CMB photons tomorrow and the day after, but they have come from slightly different places, since the CMB originated everywhere in the early Universe.
The Universe is full of CMB photons, travelling at the speed of light. When we look in a particular direction, we see the photons that were produced the light travel time ago in that direction. Let's assume for simplicity that they were made at the first instant, t=0 (in fact they last interacted with matter about 300,000 years after the Big Bang). If the Universe is say 13 billion years old, then we see the CMB photons which have been travelling towards us for 13 billion years. In a different direction we see photons arriving from a different place, which have also been travelling for 13 billion years.
Someone who is living on a planet which is about 13 billion light years away from us will be seeing CMB photons coming from where we are, if they look in our direction. Hence they can learn about what our little corner of the Universe was like 13 billion years ago. We can't see our own region at any time other than right now, but we can see a whole sphere around us that is 13 billion light years away. When we study the CMB sky we are learning about the bits of the Universe that are 13 billion light years from us, as they were 13 billion years ago. Hence a study of the CMB gives us statistical information about the very early Universe.
Does that make more sense?
I'm thinking about a potato in a microwave oven ... What does the CMB come
from? In other words, what or where is the potato that is radiating the energy?
Submitted by skelley"AT"fc.fcps.k12.va.us 11/99
The thing that is radiating the microwaves is the whole potato! That is, it's the entire Universe. If you like, you can think of us being inside an oven, which maybe was once very hot, but at the moment has a temperature of about 2.7 Kelvin. So the Universe is full of radiation that is 2.7 degrees above absolute zero - and that radiation was given off from matter when it was hot, very early in the history of the Universe.
Maybe it helps to think like this: in a regular oven the radiation comes from the hot element. Infrared radiation is emitted and travels at the speed of light, being absorbed by the walls of the oven. Now think of an oven with walls which are very far away, and which is filled with radiating hot elements. If all those were switched on and off at once then at some time later (say 1 hour) we'd see radiation coming from those parts which are (say) 1 light hour away. Everyone else in this oven will also see radiation, coming from different radiators, but basically the same thing. Now imagine this oven expanding, so that the radiation coming from distant sources of heat gets stretched on its way to you, so that it has longer wavelength, and so appears colder. If you can picture that, then you're pretty close to a full understanding of the "hot Big Bang" model of the Universe!
I want to know if it´s
possible to get the "sound" of the cosmic microwave
background radiation. Does exist some kind of
recording? How can I get it?
Submitted by manoribas"AT"yahoo.com 11/99
Someone else asked a similar question earlier. But I sense here a slightly different source of confusion.
Popular accounts of the Cosmic Microwave Background often use phrases such as "echo of the Big Bang". This is meant as an analogy, and it is unfortunate that it could be taken to imply that the CMB is somehow associated with sound waves. So let me be quite clear: the CMB is a sort of radiation which bathes the Universe and can be picked up with radio-type telescopes. These microwaves are a form of electro-magnetic radiation, like any other microwaves, and have nothing to do with sound (which are compression waves, travelling through air for example). You certainly cannot hear the CMB - unless of course you have radio antennae instead of ears!
[Response added later]
I think could be another answer like
that: "CMB peaks at about 150 GHz. Our limit for the sound is about 20
kHz. So if you divide the frequency by factor of (say) 10^7 and direct
the signal to the speaker you could hear rather noisy sound at about
15 kHz. It has something to do with the CMB."
Submitted by mvg@credit.biysk.ru
Good point. The factor by which you have to scale the CMB redio frequencies to get into the range of human perception for sound waves is about 107. Has anyone tried to simulate this and made a recording of what it sounds like?
Is the discovery of CMB a strong piece of
evidence that the universe was once much hotter than it is now?
Submitted by croswell"AT"email.unc.edu 12/99
Yes!
See the answer to some of the questions above. The simple answer is that the spectrum of the CMB indicates that it comes from something that had relaxed into very precise thermal equilibrium. The only source that we know of is the early Universe, when it was much hotter and denser. There have been other suggested origins for the CMB, proposed when the spectrum was much more crudely measured. But since the spectrum is now known very accurately, none of these alternative suggestions are even vaguely possible.
I understand that the CMB came from the "last scattering surface", which
was extremely hot. The CMB temperature (2.76K) thus cannot correspond to the
temperature of THAT surface. So what is it?
Submitted by debouche"AT"kings.edu 1/00
In an expanding Universe light gets redshifted and thereby loses energy. This is effectively the same as the "Joule-Kelvin" expansion of gases that keeps your refrigerator cool. A better way to think about it in the cosmological context is that the photons get stretched on their way to you, and are observed with a longer wavelength than they has when they were emitted. It turns out that this expansion preserves the shape of the "blackbody" radiation curve, and so the CMB appears as a blackbody with a temperature which is lower by the redshift factor between the "last scattering surface" and today, which corresponds to about 1000.
I'm looking for any pictures about noise
effects in CMB images obtained by various sky scanning methods.
Could you explain me simply what's "destriping
methods" in image processing?
Submitted by polmar"AT"pt.tizeta.it 1/00
Ah, a technical question!
The point here is that CMB maps are made by scanning over the sky in some way. So any long timescale drifts in the detectors can lead to the appearance of stripes on the sky. These reflect the geometry of the scanning strategy, and would clearly not be interpretted as being real. Nevertheless they would complicate the extraction of the cosmological signal, and hence ideally one would like to minimize such striping effects.
There are several approaches here. First of all, and most importantly, is to design the experiment to keep such long term drifts as small as possible. Secondly is to design the scanning strategy so that it is relatively easy to extract the stripes. And thirdly is to develop methods for removing the stripes from the maps - here there are many lessons to be learned from image analysis in other fields.
A great deal of work has been done recently in developing approaches to the removal of such instrumental artefacts. And a great more effort will be expended before the Planck satellite (for example) returns data. I suspect therefore, that the best methods, which are both fast and accurate, have yet to be developed. In the meantime a recent summary of some of the best work (in particular for the LFI part of Planck) can be found in the paper by Carlo Burigana and collaborators here
What about CMB polarization?
Has it been measured already?
Submitted by yurickk"AT"hotmail.com 3/00
Good question!
As well as having variations in temperature across the sky, the CMB photons are also weakly polarized. The variation in the direction of the polarization can in principle be measured, and since it depends sensitively on details of the cosmological model, then precise measurement of the polarization can lead to additional constraints on parameters of the theories.
The short answer to this question is "no". But it is expected that such measurements are not far off. There are several experiments, either existing or being built, which have the sensitivity to detect polarization on the CMB sky.
The first thing to be done will likely be a crude measurement which establishes the general strength of the polarized signal. If this turns out to conform to the standard theoretical predictions, then this will be a strong piece of evidence in support of conventional wisdom. If the results are very different, then of course that will be more exciting!
After that there will follow attempts to measure the variation of the polarization with angular scale, or in other words the polarization power spectrum (actually there is more than one power spectrum for polarization). Such measurement can help narrow down the cosmological parameters in ways beyond what is possible with just the temperature. One example if that polarization is more sensitive to a small contribution of gravity waves affecting the CMB, which may provide information about the early epoch when the initial seeds for galaxy formation were laid down. Another example is that polarization can also give a direct measurement of the epoch at which the Universe re-ionized (something that happened in the relatively recent history of the Universe due to ionizing radiation from stars and quasars). Thus polarization measurements may help unravel further details of the processes which formed structure in the Universe.
I was hoping to find a way to use the CMB in a paper I'm writing for calculus.
How is calculus used in analyzing CMB? What sort of formulas or
calculations involving calculus are used?
Submitted by blaine_5"AT"hotmail.com 4/00
This is certainly a question I've not been asked before!
Calculus is used so widely in theoretical cosmology, and in data analysis, that I've never really stopped to think of examples. Here's one for starters though: theoretical predictions for the CMB involve solving a system of equations for density variations, temperature vairations, etc. These equations are derived by considering small differences away from the average densities etc. - and so certainly this involves differentiation. To make detailed predictions for particular cosmological models you start with some simple initial conditions and then evolve to the present time - and this certainly involves integration.
These are just a couple of examples on the theoretical modelling side. The mathematical treatment of the anisotropies, and discussion of analysis methods for dealing with them, is also full to bursting with integrals and derivatives! Calculus is a way cool invention. How anyone could get through a whole day without using it is beyond me!
...if magnetic imprints of radition still exsist in the universe than can
we develope a system to harness these impulses to ...
move objects through space... (abridged)"
Submitted by goomba"AT"ismi.net 3/00
The fact that there is a Cosmic Microwave Background permeating the Universe does indeed mean that the energy density of "empty" space is not zero. There are oscillating electric and magnetic fields threading the Universe, with an equivalent temperature of about 2.73 degrees above absolute zero.
So there is certainly energy out there. But the laws of thermodynamics tell you that this energy is essentially impossible to extract as useful work. You would need to make a heat engine which was connected to something of even lower temperature! And if you tried to make something of lower temperature it would take more energy to do that than you would be able to extract. So the answer is that there's no obvious way of using the energy in the CMB to do anything like power spaceships.
But if you think of a way to do this, then you should patent it right away, since you would effectively have the perpetual motion machine that inventors have dreamed about for millenia!
How does a billion photons relate to the CMBR of 2.73K?
Submitted by Saturn1001"AT"aol.com 3/00
The CMB seems to be very well described as a "blackbody" - an ideal arrangement of photons in thermal equilibrium. The spectrum is what you get if you take a box of photons and allow them to relax, or what you get if you heat up an ideal emitter/absorber of radiation.
The point about a blackbody distribution of photons is that when you know the temperature you know everything else too: energy density, number of photons per unit volume, peak wavelength, etc. For a blackbody of temperature 2.73K, the number density is 412.77 photons per cubic centimetre.
In the Universe around us we can also try to estimate the average density of regular sorts of matter, otherwise known as baryons (meaning protons and neurons, as opposed to more exotic forms of matter). The current estimates are much less certain than for the CMB photon density, but come out around 2 × 10-7 baryons per cubic centimetre. If you take the ratio of these two densities you find that on average the Universe contains about 2 billion photons for every proton or neutron. I think this is the number you were asking about.
The photons that are observed in CMB observations have presumably been
traveling through space undisturbed since sometime after the big bang. But
thay have apparently lost energy in the process, as their wavelength has
changed. Where did this energy go? Did it go into the gravitational field?
Submitted by jamont"AT"visto.com 4/00
I'm surprised I haven't been asked this before, since it's such a good question!
There are several different ways of looking at this. One answer would be that the energy goes into the gravitational potential energy of the whole Universe. Another answer is that it takes energy to expand the Universe, and that this "work" comes out of the contents which are expanding.
Yet another answer is that the cooling of the CMB as the Universe expands is part of a simple relativisitic solution which describes the entire Universe, using the theoretical basis of General Relativity, which is a well tested theory of gravity. And if part of that solution appears to violate energy conservation, then tough!
I think that the CMR redshift z=1000 is caused by two effects.
The doppler effect because the universe is expanding.
The other effect is caused by gravity.
The matter density is decreasing because the universe is expanding so the
gravity well is decreasing so
the wavelength is increasing.
I'd like to know which effect contribute more to the redshift.
Submitted by r_lichtensh"AT"yahoo.com 4/00
The first effect is correct. Although it's better to think of an expanding Universe, rather than in terms of speeds - I'll explain. We see the CMB photons on the "last scattering surface" when they interacted with matter at z=1000 or so. What this means is that distances in the Universe were smaller by a factor of 1000 when the photons were last scattered, and they've been redshifting as they travelled through space towards us. This is more correct than thinking about a Doppler effect caused by a velocity.
The second explanation that you describe sounds like one of the important effects for generating anisotropies on the CMB sky. Variations in the gravitational potential wells on the last scattering surface (caused by variations in the density of matter at that time) lead to different redshifts and blueshifts of CMB photons, as they climb out of, or fall into, these wells. These shifts are going to be small in amplitude, since the Universe was pretty smooth back then. In fact they are about 1 part in 100,000, and this is what leads to the temperature anisotropies at large angular scales on the CMB sky.
You've just re-discovered the "Sachs-Wolfe effect"! If you'd written this before 1967, maybe it would have been named after you instead!
I am confused by calculations of the average y-distortion due to
clusters of galaxies ... (heavily abridged)
Submitted by sum"AT"rri.res.in 4/00
This is a rather technical question in detail, but let me answer it here in general terms.
The so-called "y"-parameter is a number which tells you about deviations away from a pure blackbody shape of the CMB spectrum. At some level we eventually expect to find that the CMB isn't quite a blackbody. And certainly we know that the CMB photons can have their energies changed a little as they pass through the hot electrons whizzing around in clusters of galaxies. So the total effect of this, averaged over all the sky will give a small (but eventually measurable) deviation from blackbody.
This energy-exchange through hot cluster gas is usually referred to as the Sunyaev-Zel'dovich effect, after the two Soviet theorists who first described the effect around 1970. The idea is that as the photons pass thorugh the hot cluster gas, some fraction of them scatter off the electrons, gaining some energy in the process. So when you look at the CMB through a rich cluster of galaxies you should see a small change in the spectrum, in the sense that there are slightly fewer low energy photons and slightly more higher energy photons than there should be for a blackbody spectral shape. The deviation is measured by a parameter, called "y" by Sunyaev and Zel'dovich (who derived the particular functional form of the distortion). This Sunyaev-Zel'dovich effect has now been detected for tens of individual clusters, and the study of the S-Z effect provides valuable information about the clusters themselves.
The point is that we know there are lots of clusters out there, and so we could imagine adding up all the y-distortions and averaging over the whole sky. This gives a value which is typically at least a factor of 10 below the limits which the COBE FIRAS experiment placed on such deviations from a blackbody.
Rather than measuring the average y-parameter itself, we're likely to learn more about it through deeper and deeper studies of the S-Z effect through individual cluster of galaxies, as well as through smaller groups, filaments and other structures filled with hot gas.
I just read an article that gives a
theory alternative to the Standard Model to explain the CMBR, the observable
redshift proportional to distance and the "missing matter"... the author
claims that there is diatomic hydrogen that was previously unobserved ...
(abridged)
Submitted by gazic_miles"AT"si.com 5/00
I'm all for challenging conventional wisdom. But people who do so have to do a lot of research and get their facts right before they'll be taken seriously. There are plenty of examples of changes in scientific paradigms which came about through careful study by several independent experts. I'm not aware of any major change in scientific thinking that's happened as a result of a comparative lay-person coming along with some vague idea. That's not to say that it's impossible, but just that there's an awful lot of stuff to know before you can really argue persuasively. Just as I wouldn't expect to be taken too seriously if I started arguing detailed points of law in a courtroom, someone who hasn't spent years studying physics, mathematics and astronomy, shouldn't expect to be taken too seriously when they argue about cosmology.
OK, so now that I've gotten that off my chest, let me answer your question!
It has been suggested many times that there could be more molecular hydrogen out there than expected. It is genuinely difficult to detect (although by no means entirely invisible), particularly if it is clumpy. There has been some serious study of the possibility that such clumps of cold molecular hydrogen could contribute some fraction of the dark matter in the outer parts of galaxies. However, although you can hide a lot of hydrogen this way, it's hard to make up a large fraction of the dark matter, or of the entire mass of the Universe for example. There are a number of quite firm constraints on this. So the reasonable view is that there could be more molecular hydrogen out there, but not so much that it substantially contributes to the total mass of the Universe.
You go on in your full question to discuss how you don't follow the details of this H2-explains-everything idea. And I completely agree! I don't understand at all the idea that molecular hydrogen could lead to an apparent redshifting of distant galaxies. The velocity of light would change almost imperceptibly when passing through a cloud of molecular hydrogen, so if there were any effect at all it would be incredibly tiny. Certainly there's no way to produce the redshifting factors of as high as 5 that are now seen. I also am at a loss to understand when molecular hydrogen would give a blackbody spectrum, rather than a spectrum with either emission or absorption lines of molecular hydrogen, at levels which would have been easily detectable.
In the standard model, the Universe becomes neutral at about 300,000 years after the big bang. Subsequently there are small amounts of molecular hydrogen formed (through reactions involving rare H- ions). When blobs of material gather themselves together under their own gravity and become denser (on their way to forming stars and galaxies) then 3-body reactions and more complicated processes lead to the formation of lrager amounts of H2. This molecular hydrogen is probably important for the release of internal energy from within these blobs as they cool down further and get dense enough to turn into stars etc. In this way molecular hydrogen is believed to have played an important role in the formation of the first objects that lit up the Universe many billions of years ago.
That's an exciting enough story for H2, without the need to try to get it to explain the dark matter, the CMB, and, presumably, Gamma-ray bursts, the origin of life, UFOs, the Face on Mars and the Loch Ness Monster!
I would love to know what is contained on your web page. unfortunately, the
background makes the reading of the text nearly impossible.
Submitted by DRidge"AT"aol.com 6/00
That's a problem on some combinations of computer and browser. To be honest, it's the least interesting pages that are hardest to read! You can always turn off graphics in your preferences or force an easier to read font. In other words you can try turning off the background on the internet, although you can't do that with the Cosmic Microwave Background!
When the room is empty, and everything is silent, there is a high pitch ringing
in the ears. Is this from the Big Bang? If not, what causes this?
Submitted by theodorus"AT"mad.scientist.com 7/00
Your ears are certainly not capable of detecting the Cosmic Microwave Background. Sometimes sound is used as an analogy for this radiation left over from the Big Bang - but the CMB is like radio waves rather than sound waves.
So no, that's not what you're hearing. Presumably it's something physiological to do with hearing your own circulatory system, or something like that. Although the static that you see when you tune your TV between channels is partly coming from the CMB. But you couldn't pick up TV or radio just with your ears either. Or at least most of us can't!
If you start hearing voices too, don't let me know!
Can energy be derived from cosmic radiation, much like a photovoltaic cell
does from visible light?
Submitted by enriqueromero"AT"infovia.hn 7/00
Unfortunately not. At one level this would be against the laws of thermodynamics, since is like a "thermal bath" filling the whole Universe with a temperature of about 2.73 Kelvin - so you'd need a "heat engine" colder than that to extract energy! In any case, from a practical point of view, the energy per unit volume in the CMB is minuscule by everyday standards - that's why it can pervade everything while having essentially no effects.
Could
you explain why Wien's law can be used to argue that CMBR radiation was
hotter in the past? what was this argument.
Submitted by ksawano"AT"indiana.edu 5/00
Wien's law is the property of blackbodies (i.e. ideal absorbers and emitters of radiation) which states that the wavelength of the peak of the radiation is inversely proportional to the temperature. The CMB peaks near 1 millimetre wavelength and has a temperature near 3 Kelvin. Something which is 10 times hotter than the CMB would peak at a wavelength 10 times smaller. We are at about 300 Kelvin (approximately room temperature) and our personal glow peaks at wavelengths about 100 times shorter than for the CMB, which is in the middle of the infra-red band.
There's no way of arguing from Wien's law that the Universe used to be hotter. The roughly 3 Kelvin radiation that we see could have been formed nearby at this temperature, or it could have come from an earlier time, redshifted on its way to us through the Universe, and be observed to be proportionally cooler than when it was emitted. That's what we think happened, since there's no other way of making so much energy, in every direction, and with such a good blackbody shape to its spectrum.
In the standard cosmological picture the CMB photons last scattered with matter in the Universe at about half a million years after the Big Bang. At that time the radiation was about 3000 Kelvin. The photons have been redshifted by a factor of about 1000 since then. By applying Wien's law you can then see that the CMB photons, with their wavelengths stretched by 1000, will appear as a blackbody with a temperature about 1000 times smaller, or about 3 Kelvin. It's the fact that the Universe is expanding (with freely-travelling photons having their wavelengths expanded in the process) which argues that the Universe must have been hotter in the past.
If we assume that the big bang started in a single point and was the start
of all matter in the Universe, then how do you account for CMB seeming to be
uniformly everywhere in the Universe?
There are more detailed answers to this question above. The short answer is that the Universe may indeed have started at a point, but that point was everywhere! If you could see back to the very beginning of the history of the Universe (and you almost can using the CMB), then you'd see that beginning in every direction. In other words, we're seeing the CMB radiation coming from all around us, and it all originates in the very early Universe.
As CMB can only travel at the speed of light are there parts of this
infinite Universe that are still empty of CMB and even Galaxies? If so, over
time will CMB be spread so thinly as not to be measureable?
The answer is similar to the last question. The Universe is filled with CMB radiation. The photons are moving in every direction at the speed of light, and each region of the Universe continues to be full of these photons. As the Universe expands the radiation cools, and will continue to be detectable essentially for ever, provided that you can imagine building more and more sensitive detectors.
I saw a news report about "a cloud so cold it absorbed the 3K CMB".
Could this be a misunderstanding of the Sunyaev-Zeldovich effect ?
That sounds like a good guess.
It's pretty hard to get much colder than the CMB, since it pervades everything. You can build a fridge which is one of the coldest places in the Universe for a short while (for example the bolometers which are used as CMB detectors are often cooled to about 0.1 Kelvin). But it takes energy to do this, and you can't keep those CMB photons out for ever! In other words an object won't get colder than its surroundings on its own, which is a statement of the second law of thermodynamics.
There are a couple of exceptions to this. One is in the expanding Universe at early (but not too early) times. After the matter and the radiation decoupled, but before matter was reheated by the effects of the first stars etc., it cooled more rapidly than the radiation. So there was probably a time in the history of the Universe when the matter (particularly the less dense bits) fell to below even 1 Kelvin. However, once stars, quasars and galaxies turned on the matter pretty quickly heated up to temperatures well above that of the CMB.
Another exception is in particularly dense molecular clouds. The ratio of populations of energy levels is governed by what is usually called an "excitation temperature". This can be different from the "actual" temperature of the material (usually referred to as the "kinetic temperature"). For some transitions (e.g. in formaldehyde) it's possible for this excitation temperature to be below that of the CMB. Hence one can occasionally see the line in absorption against the CMB.
In the so-called Sunyaev-Zel'dovich effect, photons travelling through the hot gas in clusters of galaxies gain energy. This means that effectively photons are taken from the low energy end of the spectrum and shifted to the high energy end. So if you started with a blackbody spectrum, then you end up with relatively fewer low energy photons and relatively more high energy photons. Since this effect is most easily studied at low energies (with radio telescopes), then what is detected when you look through a galaxy cluster is a "decrement" in the CMB. If you were speaking sloppily, then you might describe this as colder CMB. So this might explain what you read.
The way I read Plank's equations, the CMB would correspond to atoms of
hydrogen moving through intergalactic space at an average speed of just
under 250 Meters per second.... [abridged]
I do not follow your suggestion in detail. But one thing I can say is that the particles which comprise the CMB, and which have been detected in the billions by countless experiments, are certainly photons and not atoms of any sort. You can think of these photons as having been emitted by some matter which was in extraordinarily good thermal equilibrium at the time. It's extremely hard to arrange for this at recent times, for matter at close to 3 Kelvin, and quite easy to arrange for this from matter at very early times at much higher temperatures. The photons have then redshifted on their way to us, preserving their near-ideal "blackbody" spectrum, but with a much reduced temperature.
Imagining that it is a recent source of hydrogen atoms (for example) which somehow emitted the CMB photons, is an easily discounted idea. Hydrogen atoms would lead to detectable spectral lines if they existed in the required abundance, and there's also the source of the energy to explain (which is very large). More feasible would be particles of dust absorbing starlight, being heated to about 3 Kelvin, and and re-radiating the energy at microwave wavelengths. Attempts were made to model such partciles, but there are several objections. One is that there would have to be so much dust that you wouldn't be able to see distant galaxies! The second is that it seems to be impossible to invent a particular composition for the dust grains that can give nearly as good a blackbody spectrum as is observed. Hence we are left with the only viable solution: the CMB photons have a genuinely cosmic origin, and are a remnant of a hot early phase of the Universe.
1) The sun is known to produce 'solar wind' in significant amounts with
enough radial velocity for the particles (mostly hydrogen atoms) to
escape the gravity well of the sun and have some velocity left over.
2) Since the sun is not all that unusual as stars go, we can reasonably
expect that
lots of other stars are doing the same thing.
3) Adding 1) & 2) together and integrating over cosmologically long
periods of time equates to a significant amount of 'stuff' in
interstellar/intergalactic space.
4) Each of these particles is what Planck would refer to in his equations
as an 'ideal radiator.'
5) These particles readily exchange quanta of energy back and forth
between photons of microwave radiation and kinetic energy.
6) This pretty much defines the possibility of equilibrium; lots of time
and ready exchange.
Where are
there observations which disprove this development? [abridged]
This is a follow-up to the previous e-mail. I think I now understand the thrust of the question: could interstellar hydrogen be the source of the CMB?
Such ideas were certainly considered in the early history of the CMB. But it became clear fairly early on that it's impossible to have such a local source. Let me just mention a few things. One immediate problem is the isotropy: there's lots of gas in the disk of our Galaxy (and other spiral galaxies), and so we would expect to see a lot more radiation coming from the Galactic plane, and from nearby galaxies if that was the source. The second basic problem is getting the spectrum to be so close to a blackbody, and this applies for almost any material you can think of. There are several difficulties with the idea of hydrogen gas in particular. There's no reason for the gas within our Galaxy to be all at the same temperature, since the sources of heating (presumably stars etc.) vary dramatically from one part of the Galaxy to another. And hydrogen will always give a line spectrum, either absorption lines or emission lines, and that's true whether the hydrogen is mainly atomic or mainly molecular. You can look, for example, for absorption of local hydrogen in the spectrum of a distant object (like a quasar) to estimate how much hydrogen there might be in the outer regions of galaxies, for example, and you find that the answer is not very much. And it's hard to imagine that hydrogen gas distributed around our Galaxy would give anything like a blackbody spectrum.
The two basic facts about the CMB, that it is very close to isotropic, and that it is a very precise blackbody, are the things which make it very hard to explain through any local process. Hence we are led to look for a source which exists uniformly in all directions and which was in extraordinarily good thermal equilibrium. The hot Big Bang idea for the early history of the Universe makes it easy to produce the Cosmic Microwave Background which we observe.
For more discussion of this and related topics you could try to track down "The case for the relativistic hot big bang cosmology", by Peebles, Schramm, Kron & Turner, 1991, Nature, volume 532, pages 769-776. One of the most detailed studies of the failure to fit the CMB with re-radiated starlight is "Needling the Universe", by Hawkins & Wright, 1988, Astrophysical Journal, volume 324, pages 46-59.
I have recently been told about something called a "monoblock" which is
supposed to have something to do with CMB and the big bang. In all my readings
of the big bang and CMB I have never heard of a "monoblock" before.
Can you help?
Let me not pretend that I am an expert on experimental hardware! However, I believe a monoblock is a particular sort of amplifier. It is entirely possible that Penzias & Wilson used such a thing as part of their equipment which was used to detect the CMB in 1965. Can anyone else verify this?
Assumptions:
From most points in the universe, one will measure a CMBR dipole. Thus, one
would have to accelerate to attain a frame of reference "at rest" relative
to the CMBR.
Questions:
Having attained that "rest frame", would one not have to accelerate constantly
to stay at rest (to counter attraction of all the mass scattered around the
universe)? [abridged]
I think the assumption is wrong, and therefore the question doesn't need to be asked.
The fact that there's a CMB dipole (one side of the sky hotter and the other side colder than the average) tells us that we are moving at a certain speed in a certain direction with respect to the "preferred" reference frame (i.e. the one in which there is no observed dipole). To get ourselves into this dipole-free frame we just have to move with a velocity which cancels out the dipole-producing velocity. There's no need to accelerate (accept the rapid acceleration you'd need to do to change velocity of course).
Our local motion (which makes us move relative to the "CMB frame" and hence gives us a dipole to observe) is caused by nearby clusters and superclusters of galaxies pulling us around. It's true that over cosmological timescales these objects are also moving. And so if we wanted to keep ourselves always in the dipole-free frame we'd have to make small adjustments to our velocity as we moved and got pulled around by different objects. But these changes would be on roughly billion year timescales. And so to get into the frame with no CMB dipole basically just requires the following 3 steps: (1) observe today's dipole; (2) move towards the coldest direction at just the right speed to cancel the dipole; and (3) maintain basically that same velocity forever.
Why is the peak of the spectrum in the Microwave part of the
spectrum? Is it because the univers was "Hot" when created, so
radiated mostly in the IR, and has now cooled, so radiates mostly in
the microwave.
In the very early Universe things were so hot that the average photon was in the gamma-ray part of the spectrum - so much, much hotter than the infrared! It has been getting cooler and cooler as the Universe expands. Given a particualr energy density in radiation at a particular time, the temperature of the radiation is specified. The energy density (and hence the temperature) will decrease with time in the expanding Universe.
Since I have answered similar questions before, let me take this opportunity to be a little more philosophical about the vale of the CMB temperature (or peak wavelength). You can adopt one of 2 opinions: either the current temperature of the CMB is simply an empirical fact, which begs no explanation; or the fact that the background radiation currently peaks at microwave wavelengths is because we live at a particular time in the history of a universe in which there is a particular amount of radiation content. In principle one can then search for explanations for why the contents of the Universe had to be the way they are, or perhaps why we have to find ourselves living at this particular epoch. This would be an example of a so-called "anthropic" argument for the value of a particular quantity, in this case the CMB temperature. But I'm aware of no very strong argument for the current CMB temperature to be spcified at all precisely. So I'm inclined to view the CMB temperature (for now at least) as just a number to be determined by experiment.
I would like to include the "Sound" of the CMB in my talk ...
I was wondering if you had such a sound or know where I could get it.
I've answered a very similar question before. I know that one could do this in principle, although it's not clear to me that much would be achieved by playing such a sound (since you'd have to cheat in order to do this, converting electromagnetic waves to sound waves and taking liberties with the wavelengths or frequencies!). However, if anyone does know of some web-site where you can obtain such a thing, then I'd be happy to hear about it, and re-consider whether it's worthwhile after listening to the noise!
... I remember when introduced to the
idea of the photoelectric effect and the idea of photons as discrete
packets of energy ... I could visulaize them also as
little wavy worms or wavelets. Apparently you shouldn't think of photons
as being like wavelets with a sort of certain total length...
Could you please tell me what your own visualization
of a photon is? (abridged)
Submitted by biggriff"AT"biggriff.screaming.net 12/00
This is a good question, and obviously applies to all photons, not just the CMB ones.
Quantum mechanics is the theory we have to describe the behaviour of particles and fields, and the way things are on very small length scales. It is an astonishingly successful theory, and correctly accounts for an enormous number of otherwise inexplicable experimental facts. However, what quantum mechanics teaches us is that photons can be thought of as both waves and particles. This is very different from your everyday experience of sound or ripples on water (which behave like waves) and things like bowling balls or marbles (which behave like particles). On the microscopic scale things can have both particle and wave properties. Since you've never lived at the quantum scale, then there's no reason to expect that you should be able to conjure up a good mental picture for something which is both a wave and a particle.
So my answer is that I think of photons either as particles (when the particle properties are most important) or as waves (when the wave properties are most important), and I try not to think about these at the same time, because it makes my brain hurt!
If the universe in fact originated from the big bang, wouldn't
... we be at one end ...
couldn't the most distant object/galaxy/quasar we see belong to that
opposite end?
wouldn't all of the CMB have passed us long before?
Submitted by manoj.vishnubotia-eds"AT"eds.com 12/00
I get questions similar to this one all the time!
Let me make 2 points. Firstly, this Big Bang business is genuinely difficult to get your head round! Secondly, the name "Big Bang" is not the best, since it conjures up, for many people, the image of a localised explosion in space.
In fact the whole Universe is expanding, and as far as we know it is infinite in volume. So you have to try to think of the Universe beginning in a state in which everything was very much closer together, but it was still infinite! Then it all started expanding at once. We see the CMB photons coming to us from a sphere around us which is roughly the light travel distance in the age of the Universe (i.e. something like 13 billion light years) - but the rest of the Universe (that we haven't been able to see yet) is much bigger than that!
While we're talking about mental images, the best one for this purpose is to think of the Big Bang as being located on a distant sphere all around us. This is, in some sense, the opposite of the picture that many people have, and I believe this is the source of much of the confusion.
I need to know the frequency of the
cmbr in mhz or hz ect. Or maybe
Find the formula to convert K. to rf scales.Submitted by richard"AT"mcsnc.net 12/00
The CMB is a "blackbody" spectrum, which is the characteristic spectrum that you get from a body which is in equilibrium at a particular temperature. This spectrum is a broad one, and so the CMB is bright over a range of frequencies. So there isn't a single value of frequency of the cosmic microwaves.
However, for a typical CMB photon you can certainly calculate a rough
proportionality between temperature and frequency.
The average CMB photon has energy kT
(where k is "Boltzmann's constant" and T is the CMB temperature), which
is also h (where h is "Planck's
constant" and is the frequency). You can use this
to work out the approximate relationship between the typical CMB photon's
frequency and the temperature. To calculate a more precise number, you
could consider the frequency at which the the CMB spectrum has its peak
intensity. Calculating the explicit value at the intensity peak
of the CMB spectrum yields a frequency of 160.2 GHz for a temperature of
2.725 Kelvin.
How would the explosion of a major planet in our own solar system
effect the CMB?
Submitted by rboufford"AT"hotmail.com 1/01
Gosh, I've never thought about planet's exploding! I can't see that this has anything much to do with the CMB, which is much more "cosmic" than the mere explosion of a ball of rock and gas. Perhaps you are thinking of a method of forming the CMB in the solar system (an idea which certainly doesn't work, for a number of reasons)? In any case, if one of the solar system planets did somehow explode, then the radiation would be at much shorter wavelengths than microwaves, and hence it would still probably be easy to detect the CMB.
But in fact there's little chance of any planets blowing up. Collisions between minor bodies and planets are relatively frequent (on astronomical timescales at least), but it's extremely unlikely that a collision would happen with enough kinetic energy to really explode a planet. Such major collisions were part of the process that formed the planets from a bunch of smaller bodies, about 4.5 billion years ago. On the other hand the radiation that we see today as the CMB originated about 3 times longer ago than that, in the hot early phase of the whole Universe.
Do astronomers view a universe of discrete sources of
electromagnetic radiation such as galaxies, stars, gas clouds,
etc. ... Do these discrete sources radiate with the Planck
distribution until 2.7K is reached when further cooling stops, and
the sources become part of the 2.7K sink - the blackbody
radiation temperature of the universe.
Submitted by henry"AT"govital.net 1/01
If I correctly interpret this question as "what happens to an object like a star when it cools down to the CMB temperature?", then that's a pretty good question! So hoping that this is the gist of what was being asked, let me attempt an answer.
Let us focus on white dwarfs, as a concrete example. They are the end points of the evolution of stars much like the Sun, when they have exhausted their supply of nuclear fuel (and are quite close to being "ideal radiators" or "blackbodies"). A white dwarf begins as a very small (about the size of the Earth) and hot (maybe 100,000 Kelvin) lump of matter. It then cools, with no appreciable sources of energy except its heat content. Over the age of the Universe the coolest white dwarfs are now maybe 2000 Kelvin. So they've cooled down a lot, but are still pretty hot by terrestrial standards. If we were to wait trillions more years they would eventually approach the temperature of the background of the Universe (actually lower than 2.7 kelvin by that time, because the Universe would have expanded more). The white dwarf would be unable to cool any further, because it is in a "heat bath" provided by the microwave background.
Let me add that there's no way that zillions of already cool white dwarfs could explain the CMB, because there would have to be an incredibly large number of them, and we would see all sorts of related effects. There's also no way to get white dwarfs to cool down so much in only about 15 billion years.
Many astrophysicists have speculated about the last phases in the evolution of stars, and how this relates to the rest of the evolving Universe. The most thorough paper on this subject is by Fred Adams & Gregory Laughlin, "A Dying Universe: The Long Term Fate and Evolution of Astrophysical Objects", which you can get here. It's quite technical in places, but will give you a flavour of some of these fascinating ideas.
Where does background radiation come from?
Submitted by JJWALTER"AT"shrewsbury.org.uk 2/01
Everywhere!
Why is it significant that the data for the CMB shows nearly a
perfect blackbody curve? How does that help prove that the Big Bang is
the accepted beginning of the universe?
Submitted by d-davidson2"AT"northwestern.edu 2/01
The main points are: (1) the CMB appears to come from all directions and is therefore "cosmic"; (2) is it's hard to make a really good blackbody spectrum from the emission of some relatively local (e.g. cold dust in the intergalactic medium) material; (3) it's easy to make a blackbody in the early Universe, since the timescale for reaching thermal equilibrium was once very short. Hence we have to conclude that the only reasonable source of all this radiation, with such a perfect blackbody spectrum, is a hot early phase in the history of the Universe - i.e. the Big Bang model.
It's worth adding that we don't know what the "beginning of the universe" was. The hot Big Bang model is the picture in which the Universe was once very much hotter and denser and has been expanding and cooling. Exactly what happenened to start it all off is actually outside the Big Bang model, and is yet to be determined. Most cosmologists wish that the "Big Bang model" had a more accurate name!
Can you to tell me if it is possible to tune a short wave radio, let say
in a deep forest far from electromagnetic parasites, to get a clear
"sound" of the CMB?
Submitted byveau"AT"MathAppl.PolyMtl.Ca 2/01
Certainly it's possible in principle to build your own radio telescope to detect the CMB. The problem is that it's quite hard to tell that you're detecting the CMB itself and not some other source of "noise". It's not that your telescope and detector system has to be very efficient (since the CMB is in fact quite bright), but that you have to be able to confidently estimate the amount of "noise" which is coming only from the distant sky. Various electronic and other effects in your detector, thermal emission from your equipment, the atmosphere, and other sources of terrestrial radio noise will all contribute to a measurement of the "absoloute noise" level that you measure. You need to estimate and subtract all of these before convincing yourself that there's a residual source of "noise" which is the CMB.
While it's not impossible, I suspect that it's an ambitious task for a home-made radio telescope. However, I'd be delighted to be proved wrong, and for someone to describe to me a cheap and reliable method of detecting the CMB in your own back yard!
How is it calculated the reduction of temperature in function of the
expansion of the universe? Are
we sure that, during the expansion, equilibrium is always assured as
needed to get the spectrum of a black body?
Submitted ulbusi"AT"tiscalinet.it 2/01
This is a very good question, which I believe I haven't answered before!
The temperature is related to expansion very simply: there is a function
(usually called the "scale factor") which determines how distances are
changing in the expanding Universe. The temperature is just inversely
proportional to this function. It turns out that if we use redshift (usually
denoted z) as a way of measuring times back into the past (z=0 is today, and
increasing redshifts are earlier in the history of the Universe), then
T
(1+z).
It's relatively easy to show that in the expnading Universe the background radiation retains its equilibrium (blackbody) spectrum. So a hot blackbody of several thousand Kelvin at high redshift is seen as the much cooler CMB (and still blackbody) today.
How come radiation "cools off" instead of retaining a constant
wavelength?
Submitted plotinus"AT"otenet.gr 2/01
You can think of this just like any other form of slow expansion of a gas. Expansion acts to cool a gas, which is for example, the principle on which refrigerators work. Physicists refer to this as "adiabatic expansion". You can think of the CMB as a gas of photons, adiabatically expanding through the Hubble expansion of the Universe. This photon gas loses energy. And since the energy of a photon is inversely proportional to wavelength (Planck's law), then the wavelength increases as the Universe expands.
Another way to think about this is just that the wavelengths of the photons stretch along with all the other distances - the interpretation of cosmological redshift is just that when the photons left their source, distances were proportionally smaller, and the wavelengths got stretched (i.e. redshifted) on their way to us.
I know the GZK limit is supposed to limit the energy of the cosmic
radiation incident on Earth to under 10 to 20 eV or so. It has to do
with special relativity and CMB. But that is all I know about it.
Could you explain what it is, or point me to papers/references that can.
Submitted kelleigh"AT"look.ca 2/01
The "GZK cut-off" or "GZK limit" is an effect on high energy cosmic rays due to the possibility of scattering off CMB photons. GZK stands for Greisen-Zatespin-Kusmin, who pointed out the effect in papers in 1966. The idea is that the highest energy Cosmic Rays (let's abbreviate to CRs) are moving so fast that in their rest-frame the CMB photons are extremely high energy. Most Cosmic Rays are simply protons, i.e. the nuclei of hydrogen atoms. If so, then there's the possibility of conversion of the pair of particles (CMB photon plus CR proton) into a pair of other light particles, like pions. Calculations show that what you need is for the energy of the CMB photon plus the Cosmic Ray to be bigger than the rest mass energy of a couple of pions, in the centre of momentum frame, which effectively happens when (ECMB × ECR)1/2 = 2mpionc2. There are so many CMB photons that CR's with the highest measured energies (above 1020eV) can't get very far in the Universe, and so the energy spectrum of CRs should be heavily attentuated above these energies.
That there are detectable CRs above the GZK cut-off (found using detectors which measure showers of particles casued by these CRs hitting the upper atmosphere) is one of the big mysteries in present-day astrophysics. Scientists are currently divided about whether or not this mystery can be resolved with known physical effects, or whether it needs some whole new physics concept.
There's a lot of information available on the web on ths topic. You could try searching for "cosmic rays", "ultra high energy" and "GZK", but a good place to start might be http://www.cosmic-ray.org/
Why don't we see cosmic background radiation well into wavelengths
longer than microwave? I understand the concept of "last-scattering
surface" and its relevance to why we don't see *shorter* cosmic
background wavelengths, but I don't understand why we shouldn't also
"see" longer wavelength remnants of an even younger, more redshifted
universe.
Submitted by bozone"AT"ripco.net 4/01
Remember that the photons are red-shifting on their way to us. In principle we can't tell the difference between photons emitted very early, which have redshifted a lot, and photons emitted later, which haven't redshifted so much. The early Universe is hotter and hotter. And this is balanced exactly by the redshift factor.
The "last-scattering surface" is not the time when the radiation formed, just when it last interacted strongly with matter. At that time they were redshifted by about a factor of 1000, and at a temperature of about 3000 Kelvin. But before that they would have been at 30,000 Kelvin, and redshifted by a factor of 10,000 on their way to us. And before that they would have been at 3000,000 Kelvin, and redshifted by a factor of 100,000. Etc.
Is there any way to be sure that the CMB fills the entire
universe? Isnt it possible that it only exists around certain entities
(perhaps it only exists around Earth, for that matter)?
Submitted by whitetrash_01"AT"hotmail.com 4/01
Obviously we only have direct information about CMB photons which have arrived at detectors right here on Earth. But they had to come from somewhere at the speed of light! Since they're observed to come from all directions, then everywhere in the Universe seems likely to be filled with these things. The only way to avoid that conclusion would be to have all the photons aimed at us, and that puts us in a very special position indeed! That would contradict the observation of zilllions of galaxies in the Universe, which show that our local part of space isn't much different from any other.
There are also some fairly direct ways of showing that the CMB photons exist elsewhere. One way is to find the effect on the CMB of the photons having changed their energies a little as they travel through the hot gas in a cluster of galaxies. This effect has been measured for many distant galaxy clusters, indicating that the CMB photons have to be coming from at least as far away as those objects.
The observation of structures (anisotropy) on the CMB sky is also good evidence for a Universe filled with CMB photons. That's because the size distribution of the structures on the CMB sky has turned out to be just like you'd predict in the hot Big Bang model, where the CMB photons are in fact left over from a much hotter early phase of the history of the Universe.
Since the CMB is microwave radiation it must travel at the speed of light, or
300,000 km/sec. Question: in what direction is it traveling? Any radiation
with which I am familiar it has a source and hence a direction of
propagation. Do these terms have any meaning re the CMB?
Submitted by DDKavanagh"AT"aol.com 4/01
The best way to think about this is that the CMB is emitted from everywhere in the early Universe, travelling in all directions (and don't make the mistake of thinking of the early Universe as smaller, since that will give you entirey the wrong mental picture!). We see the CMB photons coming at us from different parts of the early Universe, in all directions around us. In other words there's a sphere around us giving the location of the places where the photons came from. And from the locations on that sphere we only see those photons travelling in our direction. But there's nothing special about where we are, since other observers would think about their own (different) sphere, and detect photons coming from other places, or some of the same places but in different directions.
So the photons are indeed travelling at the speed of light. But they have no special direction in which they travel. They are emitted in all directions (like the Sun, or a round light-bulb) by matter in the early Universe, which was everywhere!
Who discovered the CMB anisotropy?
Submitted by bowenj01"AT"hotmail.com 5/01
The detection of CMB anisotropy was announced by the COsmic Background Explorer (COBE) team in 1992. Other experimental groups had data at the time which contained weak anisotropy signals. The measurements are sufficiently hardthat all the experiments up until COBE had quoted their results as upper limits. It required the robustness of a careful year-long set of space-based data before anyone could be confident of detection of the anisotropy. COBE was a huge team effort, with the Principle Investigator of the relevant instrument (the DMR) being George Smoot. The first person to have convincingly demonstrated that anisotropy existed in the data was probably Ned Wright. Many other scientists, engineers and support staff were involved in the effort, and it was the quality of the COBE data that enabled the discovery to be made.
has any one considered (even though I can't fathom its
existance) this dark energy/matter fluctuation as the source of the CMB
and could it be possible that this "exotic" phenomenon only causes
photon radiation at the microwave energies observed?
Submitted by wjw"AT"bellsouth.net 5/01
I haven't seen any suggestion along those lines.
To be honest though, there's no real motivation for looking for such an explanation. The CMB makes lots of sense as the remnant of the earlier hot stage of the expanding Universe. So if you want to think of some source which avoids the hot Big Bang idea, then you throw away a lot of other things too. In particular most of the evidence for dark energy (although not dark matter, for which there is good evidence on relatively local scales) is in the context of the Big Bang picture. Without that picture it's unclear what you do with the expansion of the Universe, the dimming of supernovae, the angular scale of CMB ansiotropies, and many other empirical observations.
CMB photons originates with the Big Bang. At the time of CMB creation the
universe was relatively small. CMB radiation is now received from all
directions. How is this possible, as radiation is now received from points
in space at which no material (particles and anti-particles) existed during
the time of the Big Bang?
Submitted by chris.ungerer"AT"quintiles.com 6/01
Let me try to answer by disecting your question.
"CMB photons originates with the Big Bang" - this is more or less true. Actually there are photons existing quite early on, and the ones we see were effectively created about a year after the beginning. But that's pretty short on a cosmological timescale!
"At the time of CMB creation the universe was relatively small" - this is the main source of difficulty. The Universe wasn't smaller. It was still big enough that considering it to be infinite is a pretty good approximation! It's just that things used to be closer together.
"CMB radiation is now received from all directions" - true, and it's almost the same brightness in every direction.
"radiation is now received from points at which no material existed during the Big Bang" - this isn't true (see above). However, I think what you might be getting close to here is what cosmologists refer to as the "Horizon Problem". This is the realization that as the Universe gets older, the region over which light can have travelled gets bigger. No physical process that we know about can operate faster than the speed of light, and so this light travel distance is the largest scale over which anything can have had an effect on anything else. This now corresponds to the most distant objects we can see. But the problem is thast this distance used to be much smaller. So when the CMB photons were produced one part of the sky that we see wasn't in contact with another. And then it's mysterious that the CMB temperature "knows" to be the same over the whole sky. How come?
The most popular answer is that the Universe once underwent very rapid expansion, so that the distance over which things could affect each other grew tremendously huge. Then our whole observable volume is within a region that was once in contact with the whole of itself. Ths idea is called "inflation" and is one of the most promising ideas for understanding what might have happened in the very very early history of the Universe.
I hope the summary of a non-expanding universe attached,
will hold enough interest for you to include in your extensive
coverage of the CMB. All the requiredments for standing waves
seem to be present here as well as the characteristics of the
electromagnetic waves in the 2.7K CMB. [abridged]
Submitted by henry"AT"govital.net 8/01
I don't understand what you mean by the CMB being "standing waves", a topic I addressed elsewhere on this page. Experimentally the CMB consists of radiation travelling at the speed of light, and observable in every direction.
Evidence that the Universe is expanding has been rather compelling since it was discovered by Hubble in the 1920s. Some other ideas to explain the measured redshifts of distant objects have been proposed over the intervening decades, but all have long since fallen by the wayside. The "Hubble diagram" (recession velocity versus independently estimated distance) now extends over about two orders of magnitude greater distances than probed by Hubble.
The main reason to believe that the Universe is genuinely expanding is that by making this assumption you build a self-consistent picture for understanding distant objects, and that no observation has turned up to contradict that picture. There is now a huge set of inter-related cosmological phenomena which make sense within the expanding Universe paradigm.
But if you don't like the argument of interleaved self-consistency, there's also direct observational evidence for expansion through measurements of the CMB temperature at high redshift. The technique is to use intensities of atomic lines in the spectra of distant objects to infer the CMB temperature long ago when all distances in the Universe were smaller. The results are that the temperature of the CMB is higher in the past, just as it should be if the Universe is expanding.
Does the CMB create a universal rest frame? i.e., by using the redshift
of the CMB can we determine our motion with respect to the "rest frame of
the universe"? What about special relativity?
Submitted by saul"AT"excite.com 9/01
I'm sure I've answered this before, but it's a good question!
Yes, the CMB defines a rest frame, and we can determine our motion relative to that frame.
There are two answers to the special relativity part of this question: (1) the Universe is described by General Relativity, which applies for accelerated frames as well as inertial ones, so there's no reason to expect special relativity to hold; (2) the only problem in Relativity would be in having a frame which is special for the laws of Physics, and the CMB rest frame isn't any more special than other frames in that regard.
i have tried to understand it, but i am so
confused since there are so many different things about cosmic radiation from
hps or books. i think every book is talking different things, i cannot make a
conclusion. can u give me some hints about how to summarize those points?
[abridged]
Submitted by skchan3"AT"csis.hku.hk 10/01
This is another question which (a) appears to be asking me to do homework for someone! and (b) is confused about the difference between the CMB and Cosmic Rays (both of which might be called "Cosmic Radiation").
In fact I received this email 3 separate times. So let me answer as follows: Cosmic Cosmic Cosmic Rays Rays Rays and and and the the the CMB CMB CMB are are are different different different things things things entirely entirely entirely. Three of them are high energy partcles from space, while the other three are low energy photons from the early Universe!
If the Universe was much smaller when it became transparent, the matter
that forms our galaxy today was much closer to the last-scattering
surface. So how it comes that the CMB photons are reaching us only
today? How did we move faster than these photons that they are reaching
us now?
Submitted by thalesc"AT"uol.com.br 10/01
The Universe was not much smaller in the past! The Universe is expanding (we know that empirically), so that everything was closer together in the past. But the Universe should not be thought of as a finite-sized object embedded in space (the Universe is space!). Infinity is a tricky concept to grasp - but if the Universe is infinite in size, then it was infinite before, it's just that everything used to be closer together. So there are always places which were far enough away from us at the time of last scattering that their photons are just reaching us now.
This question probably represents the single greatest difficulty people have in trying to understand the expanding Universe. I think if you start by erasing the notion that the Universe used to be smaller, then you go a long way towards sorting this out. But let me not pretend that it's easy to grasp the notion of an infinite space which is expanding!
The concept of an infinite and expanding Universe is not that hard to
understand. However, it's hard to conciliate with the notion that the
Universe is limited in terms of energy/matter, _if_ this notion is indeed
correct. [abridged]
Submitted by thalesc"AT"uol.com.br 10/01
The energy density of normal matter, dark matter and dark energy (or vacuum energy if you like) are all finite. In other words the energy per unit volume is a measurable thing, and indeed that's the quantity that cosmologists are trying precisely to measure for each of those 3 cosmic components.
But if the Universe is truly infinite in volume, then the total energy content would presumably be infinite too! Out to the edge of the observable part of the Universe (where light can have travelled in the age of the Universe) it's perfectly finite of course. But in principle one imagines an infinite amount more of the same out there!
Do I understand properly that up until the universe was 300000 years old,
matter was all so hot that it was emitting high-energy radiation, and that
this radiation is what we now call the CMB?
Submitted by Bore"AT"BoringSoftware.com 10/01
That's an easy one! YES!
I hate to ask it again ... but why hasn't the CMB all gone "past" us yet?
My mental picture is that all matter in the universe
stopped radiating this energy at some point. I don't have a clue how "large"
the universe would have been at that point, but I'm assuming less than a
billion light years in diameter. So if those photons have been traveling for
(conservatively) almost 12 billion years, it seems to me they would have
crossed the entire universe to somewhere else by now. [abridged]
Submitted by Bore"AT"BoringSoftware.com 10/01
This is harder to answer. I know this, since I've tried to answer it as carefully as I can several times before. Some concepts are genuinely difficlut to grasp, and this seems to be one of them. So please bear with me here.
The trick, I think, is to stop picturing the Universe as finite. The photons would sort of pass everything if the Universe was a little lump of stuff embedded in empty space. But the Universe is everything remember. Assuming it's infinite (or at least big enough that we've only seen a very small part so far), then there's plenty of parts of the Universe which were far enough away during the early phases of the "Big Bang" that their photons haven't reached us yet. The CMB photons that we do see today are those that originated the speed of light times the age of the Universe (roughly) away from us. Tomorrow we'll see those that originated one light day farther away from us, and so on.
Can I get the sound of the CMB? [abridged]
Submitted by dsal1111"AT"netzero.net 10/01
I already discussed that above. The short answer is that it's not a "sound", but in principle you could use some artistic license to convert the electromagnetic "blackbody" spectrum to a spectrum of sound waves.
Let me know if you manage to find or make such a recording yourself. I'd also like to get a copy!
I am an artist and am in need of a sound recording
of galactic background radiation for an installation I
am working on.
Submitted by michael_wynne"AT"yahoo.com 11/01
I've answered similar questions above, but this is slightly different.
When we look for detailed information about the CMB, anything that gets in the way can confuse the picture, and we refer to those confusing signals as `foregrounds'. One obvious foreground is emission from our own Galaxy, the Milky Way. This gives particularly strong signals in the plane of the Milky Way, and fairly negligible signals when we point well away from the plane.
The signals themselves can be measured with a radio telescope, and in fact the radio hiss from the Galaxy was the first astronomical signal measured on Earth (apart from emission from the Sun). So the signal is pretty strong.
Radio signals are fluctuation electric and magnetic fields travelling through space. They are not sound waves. However, if you wanted to represent the radio wavelengths as sound wavelengths, you could certainly do that. So there's nothing to stop you putting the spectrum of the Galaxy through a speaker. You might have to fiddle the wavelength scale a bit to get sound waves in the best range for the human ear. But since this is for fun, you get to use that artistic licence!
At least the signals from the Galaxy will be more interesting than just the CMB! The CMB is so nearly a "blackbody" spectrum that there wouldn't be much in the way of interest in the noise it makes! "Hearing" the sound of a radio telescope scanning across the plane of the Galaxy could be quite intriguing though. Particularly if you heard the odd pulsar, since those actually pulse in time and so would give some added variation.
One artist who has been specialising in music inspired by "astronomical noise" is Fiorella Terenzi. Her web page is here.
What would happen when the CMB temperature reaches 0.00 degrees Kelvin?
Would this signal the end of expansion of the universe?
Submitted by bfayeh"AT"msn.com 12/01
In a sense you are right. Although of course the Universe will never quite reach absolute zero. It will just get colder and colder and colder. It will only apporach zero as the time approaches infinity.
If the Universe is dominated by "Dark Energy" and now accelerating (as many cosmologists now believe), then the temperature will decrease exponentially fast. In other words at some point when the temperature is say 0.001 Kelvin, then if you wait some amount of time it will have become 0.0001, while if you wait twice that time it will already be only 0.00001, etc. So it will get ever smaller by the same factor in each fixed time interval. But still it will take an infinite amount of time to get all the way to zero.
Long before the CMB gets to zero Kelvin though, any instrument you can imagine making will have a near impossible time detecting it. And in general the Universe will have become a pretty empty and boring place for you!
The Big Bang is wrong because of this very interesting numerology!
sin 60o x SQRT(10) = 2.738 which agrees up to measurement
error with the temperature of the CMB in Kelvins. [abridged]
Submitted by orlandodelavega"AT"terra.es 12/01
Numerology is not very powerful, unless there is some physical explanation lurking there. You should have a look at my own numerological ideas for generating the CMB temperature here.
And incidentally, the best measurement of the CMB temperature currently is 2.725 Kelvin.
if I am sitting inside of a commercial aircraft, and all the passengers have
their windows closed so that I cannot see what is outside of the cabin,
can I determine the speed of the plane relative to the CMB?
Submitted by dellaenterprises"AT"prodigy.net 12/01
If you really coudn't see out of the plane, in microwaves as well as in visible light, then you couldn't tell.
So to make things simpler, let's assume that you are somewhere in open space in a rocket, and you'd like to know your "absolute" motion relative to the CMB. Then all you do is build a CMB mapping experiment and map the whole sky (some fraction, or even just a few pointings would do). Then you can tell that you're travelling towards the direction in which the sky appears hottest, and away from the direction it appears coldest. And the speed is just determined by the amplitude of the temperature difference that you see (so that the fraction of the speed of light is just the fractional amplitude of the temperature change).
What will eventually happen to the CMB? That is, the CMB photons have
been stretched (cooled) down to the microwave level at this point. What
will happen in the coming billions of years? Will the CMB eventually
become the "Cosmic radio wave background" and then the "Cosmic (what's
lower than radio waves?) Background?"
Submitted by rreeves"AT"winfirst.com 1/02
Exactly right!
Currently favoured models have the Universe expanding forever. In that case the CMB photons get stretched further and further, so they have lower and lower energy and we'll measure an ever decreasing temperature. There's no limit to how low the energy of a radio wave can be - so after it's the Cosmic Radio Background it will be the cooler CRB forever!
...I began to wonder if this stuff might still be around.
(A proton/negative-muon pair, or muon/negative muon pair has such a
high ionization energy, ~ 2.81 keV, it would be hard to crack.) So I
did a rough calculation of where the 21.1 cm hydrogen line would be
shifted when the electron is replaced by a muon (m ~ 105.6 MeV) to get
0.1 cm or about 294 GHz. ...
Then I came to your site,
and found the peak is rather near your CMB peak. All of the curve would be
identical, just the coefficient would be based on the muon mass rather
than the electron mass.
Submitted by Director"AT"TheInternetFoundation.Org 12/01
This is rather an interesting idea, but as far as I can make out there are a number or rather fatal flaws!
Firstly, as you point out yourself, muons are very unstable, so there's no reason to believe there are any left from the early Universe.
Secondly, if the CMB arises from line emission from material distributed through space, then it must be emitting through being excited by some local process. And then you'd expect to see quite different brightnesses in different directions, depending on the local conditions etc.
Thirdly, if it's a line emitting process, then there's no reason to expect anything like a "blackbody" shape for the spectrum. The natural line-width will be negligible, so the breadth of the spectrum needs to produced by local effects like velocities or something. Again you'd expect this to vary with position. And it wouldn't give a nice blackbody spectrum.
On the other hand, in the conventional picture there were lots of primordial muons and anti-muons at early times in the history of the Universe. But they annihilated when the temperature was roughly equal to their rest mass. In fact a significant fraction of the CMB photons were created in this annihilation. And so there certainly is a connection between the CMB and muons.
If the universe was far smaller then and everything
closer together, and if nothing can move faster than
the speed of light, why has the light taken 14bn years
to get here? Wouldn't it have overtaken us on the way
out?
Submitted by themanwhogrowstrees"AT"yahoo.co.uk 1/02
This is a very good question, and probably the most common question asked about the CMB (phrased in one form or another). You can find longer answers by searching on this page. But the short answer is that the first statement you make in your question is incorrect!
what IS Cosmic Microwave background Radiation??
Submitted by sworku"AT"sympatico.ca 1/02
Strangely enough, no one has really asked that question before!
For more detail you should go up to the Basic questions page.
For now, let me say that it's a very cool glow that permeates the Universe, and provides us with a glimpse of a very hot early epoch in cosmic history.
Why doesn't the CMB spectrum have artifacts from earlier hydrogen or helium
absorption/emission, say from when it was around 8000 K hot?
Submitted by j.cotter"AT"unsw.edu.au 2/02
This is a truly excellent question!
We believe that the CMB spectrum does indeed contain deviations from a pure blackbody, because of the interactions of the hydrogen and helium. But they're at such a low level, and in the low energy tail of the spectrum, that it's incredibly hard to imagine how you might detect such a signal.
Basically each hydrogen or helium atom gives off a few photons of specific energy as they become neutral. These distort the CMB spectrum, to give little bumps on top of the blackbody shape. But remember that there are about a billion CMB photons for every atom in the Universe. So the distortion to the spectrum is very tiny. It also turns out that it's biggest in the far-infrared part of the spectrum, where it is swamped by signals from our own Galaxy and emission from other galaxies.
It would be really cool to detect these bumps though, because then you'd have absolutely cast0iron proof that the Universe went from an ionized to neutral state. And if you could ever study the bumps in detail, you could learn precisely how this process happened.
What effect does starlight - normal star photon radiation
-(not cosmic particle radiation, not the cosmic wind )- have on the
CMB? ... would that CMB
temperature increase be due to scattering from electromagnetic
interaction with star photon radiation? [abridged]
Submitted by rreeves"AT"winfirst.com 2/02
Signals from stars and galaxies, dust, gas clouds, etc. affect observations of the CMB, but have quite different spectra. So they can be distinguished and removed. CMB people talk about the need for removing "foreground" emission so they can cleanly get at the background signal.
But these radiations don't affect the actual CMB photons themselves. The interaction rate for a starlight photon to interact with the CMB is incredibly small. So your average photon from the Sun, say, will travel across the whole observable Universe without interacting with a CMB photon. This means that the "foreground" signals simply add to the CMB signal, with no complicated interaction effects.
Where goes the energy of a red Doppler-shifted photon when it arrives at a
receding destination?
Submitted by j.cotter"AT"unsw.edu.au 2/02
Actually this is just a more sophiticated version of the question "where does the energy of a redshifting CMB photon go as the Universe expands?"
The answer is, in a sense, that it goes into the expansion of the Universe.
My question is about the following quote from your website: ". That radiation
cooled and is now at 2.7 Kelvin. "
What do you mean? Do you mean it red-shifted? Do you mean it actually cooled.
Submitted by glenstaples"AT"shaw.ca 2/02
That's the same thing!
An expanding gas cools. In just the same way, an expanding "gas" of radiation cools. You can also think of each photon being redshifted and so having a lower energy when you observe it than it did when it was emitted. So in an expanding universe we see the hot radiation from early times as cool radiation today.
if looking into the microwave while it's turned on (ie. microwaving food),
has negative affects on people, health wise?
Submitted by msoczewinska"AT"email.com 3/02
There are many sites where you can look up information on microwave ovens. And this isn't one of them!
The short answer is of course "no". The mesh around the oven prevents almost all the microwaves leaking out, and there's a mechanism to prevent it being on with the door open.
Besides which, only strong doses of microwaves are harmful. We know this because we're bathed in Cosmic Microwaves all the time!
How effectively is microwave radiation absorbed by rocks (silicates)?
Submitted by ray"AT"bisque.com 3/02
No idea! (see answer to the above question, and several others here).
Although I do know that it would be a poor experimental design for a CMB experiment to build it underground!
How many CMB photons are there in the visible universe?
Submitted by j.cotter"AT"unsw.edu.au 3/02
The radius of the observable Universe is about 10,000 Megaparsec (or about 3 × 1026 metres). And the shape is just a sphere with us at the centre. The CMB contains about 400 photons per cm3. You can work it out for youself!
How does the vacuum energy density relate to the cosmic microwave
background energy density?
Submitted by ogressel"AT"uoguelph.ca 3/02
There's no direct relationship between them.
Interms of the contribution to the critical energy denisty required to make the geometry of the Universe "flat", vacuum energy is believed to contribute about 2/3, while the CMB contributes about 0.005 of a percent.
It's important to realise though, that in an expanding universe, the vacuum energy has only been dominant at relatively recent times. And that if you go back early enough the radiation dominates over regular matter too. So the early Universe was the domain of radiation, but its time is long over. Fortunately the CMB still retains some information about those early epochs.
I don't quite understand why the temperature of
the microwave radiation would be 2.73. where does this number come from?
Submitted by slmcph"AT"mta.ca 3/02
The number comes from direct measurement of the distribution of energies of the CMB photons. That distribution follows precisely what you expect from something at a single temperature (a lot of photons at some characteristic energy, with the numbers falling off in a known way at both high and low energies, and this characteristic energy tells you the temperature).
It's purely an emprical number. There's no obvious way of determining what the CMB temperature should be - you just have to measure it!
Was the CMB created when energetic photons ionized the neutral hydrogen
atoms that originally filled the universe or not?
Submitted by weberma"AT"w.imap.itd.umich.edu 4/02
No.
The CMB photons were created at a much earlier time, when the Universe was very very hot. There are about a billion photons in the Universe for every hydrogen atom. So when the Universe cooled enough for the hydrogen to become neutral, there was a tiny little extra bit of the CMB created, it's true, but it was only about a billionth of the CMB as a whole!
How do we know that the early universe was a blackbody?
If CMB is our best shot at proving the big bang, presumably we assume that
the blackbody spectrum observed is what you would expect from an exploding
blackbody?
Submitted by anne.laking"AT"bbc.co.uk 4/02
What we know is that the spectrum of the CMB today is extremely close to blackbody in shape. And that in an expanding medium the blackbody spectrum retains its shape exactly. The peak wavelength increases as the medium expands, but the shape remains the same. Plus, we also know that the Universe is expanding.
So if the CMB has a blackbody spectrum now, then it has retained that spectral shape from early times. It used to be hotter, but still a blackbody.
We can estimate what must have been going on at very early times, using what we know about nuclear and particle physics. It turns out that the interactions among particles were sufficiently rapid that all the constiuents of the Universe must have been in very good thermal equilibrium. In other words the spectrum starts out as a blackbody. Or to turn it on its head, the fact that its a blackbody today is most easily explained in a picture where the Universe used to be very much hotter and denser.
We don't know precisely what started the Universe off, or what it's state was in the first zillionth of a second. But as far as the CMB is concerned, the observed blackbody nature, together with the observed expansion of the Universe, means that we know the Universe was once very much hotter and denser. What started the Big Bang is still a mystery, but we have a pretty good idea of what the Universe has been up to since then!
I wonder if you can tell me if there are some mailing lists on Cosmology
and CMB, I suppose there must be at least one. I'd like to be a member
if there is one (or more !).
Is there any newsgroup too ?
Submitted by ss5946"AT"garnet.acns.fsu.edu 5/02
I'm not aware of any email distribution list for people interested in Cosmology and/or the CMB. You could always start one of course! But I suspect most people are like me, and don't really want more email! So probably what you are looking for is a discussion group, and obviously there's nothing stopping you setting up a "cosmic chat-room" if one doesn't exist already. Does anyone know of one?
As far as newsgroups go, the closest thing is sci.astro and sci.space.science.
Would it be possible to detect spectral lines in the CMB? Sometime in
the early universe, the CMB would have been CLB (Cosmic Light Background),
and many elements and chemical compounds have spectral absorbtion (or
emmission) lines in or around the wavelengths we associate with light.
I take it these
spectral absorbtion lines would be stretched along with the radiation
itself, and would be still detectable.
Submitted by Ralph.Newnam"AT"sunrise.net 5/02
This is an excellent question!
The basic answer is that it's possible, although very difficult to detect such lines. And since the early Universe consists almost entirely of hydrogen and helium, then those are the only elements which are feasible. One can calculate the spectrum of hydrogen and helium lines produced as the Universe became neutral. However, the thing to bear in mind is that there are about a billion CMB photons for every proton in the Universe - so the lines are incredibly weak! On top of that they're also quite broad, making them even harder to detect. However, the lines are a very definite prediction of the hot Big Bang picture, and so unless it is prohibitively difficult (because of contamination by nearby material for example) presumably one day they will be detected.
I understand the logic in saying that CMB must have come from a
nearly perfect black body, but where did they get the initial temperature? The
temperature currently quoted is 2.73 K.
How do they work back to show that this 2.73K came from something so much
hotter?
Submitted by Richard.Kingsley"AT"wtel.tdsb.on.ca 7/02
The present-day temperature of the CMB is about 2.7 Kelvin, i.e. less than 3 degrees above absolute zero.
One fact that we've known about the Universe since the 1920s is that it's expanding. Radiation in an expanding medium cools (just like the gases used to provide the cooling in some refrigeration systems). So in the distant past, when everything in the Universe was much closer together, the CMB radiation must have been very much hotter. Another way to think of this is that the wavelengths of the CMB photons just expand along with everything else in the expanding Universe, and longer wavelengths mean lower energy photons and hence cooler radiation.
Once you accept that the Universe is expanding (and so when you run backwards in time everything is denser and hotter), then you can ask about the origin of the CMB radiation. It turns out that in a hot dense radiation-filled universe, the time for the radiation to reach equilibrium is very much shorter than the time the Universe takes to expand a significant amount. So this early Universe radiation would be predicted to have been in very good thermal equilibrium. And that means that we should observe it to have very close to a blackbody spectrum.
So the blackbody nature of the CMB (together with the expansion implied by the redshifts of distant galaxies) points towards the Universe once being very much hotter and denser than it is now.
[abridged] what frequency corresponds to this temp. of 2.7 K - 163 Ghz?
Submitted by glennmr2002"AT"hotmail.com 7/02
The CMB has a blackbody spectrum. That means that the photons have a distribution of frequencies of a well known shape, having a characteristic frequency. So there is no specific frequency corresponding to the CMB temperature. The answer will depend on whether you want the average frequency of all the CMB radiation, or the frequency where intensity per unit frequency peaks, or intensity per unit wavelength, or whatever.
The intensity per unit frequency quantity peaks at about 160 GHz for a 2.725 Kelvin blackbody.
I'm having a little trouble with the idea of warming a (near)
vacuum by irradiating it with infrared radiation. [abridged]
Submitted by nibblett"AT"juno.com 10/02
The CMB consists of a "gas" of photons moving at the speed of light, not a regular gas of atoms or molecules. So the thing that's at 2.725 Kelvin is the photons and not the diffuse material in space. What this means is that it's extremely hard to imagine any matter in the Universe being colder than this (since it's being exposed to this "bath" of photons), but it's easy for matter to be much hotter, because of other local processes (like hot stars, explosions, etc.).
Initially I hope I am right in saying the universe was a plasma and photons
exchanged energy between the charged particles.
Then protons and neutrons started forming atoms and the photons become
trasparent if you like.
Is this not a violation of the laws of entropy as the universe wants to
become more and more disordered where as in this case there seems to be a
decrease in entropy.
Submitted by colesthemonkeyman"AT"hotmail.com 11/02
There is no decrease in entropy. As you say, the second law of thermodynamics seems to be quite fundamental, and tells us that entropy can never decrease. When considering the whole Universe, one normally thinks about quantities per unit volume as that volume expands. The total density of entropy certainly does not decrease in the expanding universe picture.
The formation of neutral atoms from a plasma is not a process which reduces the total entropy. Entropy doesn't mean "disorder" in a vague sense, but is actually a well defined physical quantity, related to disorder but fully quantifiable. When an electron combines with a proton the total entropy either stays the same or increases. Remember that there's also a photon emitted in this process.
In fact the entropy density in an average part of the Universe is dominated by the entropy in the CMB photons. And conservation of this entropy is actually used to simplify some calculations (which you can find in standard cosmology textbooks). So the second law of thermodynamics is built in to the whole Big Bang picture.
Is it possible that background Radiation is produced by eletron/positron
destruction in blackholes and then ejected out.
Submitted by Johnnypetra"AT"aol.com 11/02
If you mean "could the CMB be produced through evaporation of some local black holes", then no that isn't possible.
If there were lots of small black holes around and they were evaporating, then they'd give off high energy gamma-rays. Larger black holes which emit microwaves would be far too weak. Or you'd need them to be filling the Universe, and so they'd be obvious in other ways. And there's no way of getting an accurately thermal spectrum which is the same in every direction.
However, there is some aspect of truth in what you suggest. We believe that the CMB photons came from a time in which the photons were in equilibrium with the other particles in the early Universe. And extra photons were added to the background when most of the electrons and positrons annihilated (somewhere around a second after the Big Bang).
It's also possible to have exotic things happen in the very early Universe which could also add to today's observed CMB. Anything you do before a time of about 1 year tends to get thermalised (i.e. looks like a blackbody spectrum even if it started off completely different). So if you imagined some black holes decaying at early times and giving lots of gamma-rays, then if it happened early enough it would be hard to tell.
The background radiation is energy of course -- and it is everywhere,
presumably filling the universe, as you say. Energy and matter are
equivalent in some sense. Is the mass of this energy taken into account
in determinations if the universe will forever expand or will someday
collapse?
Submitted by Arsen"AT"marketsize.com 11/02
Yes it is, but it doesn't make much difference. The models used are done within the framework of General Relativity, which includes all the ideas of Special Relativity, e.g. the equivalence of mass and energy.
The mass-equivalent density of the CMB is about 10,000 times smaller today than the amount of matter inferred from observations. So it has very little effect on the expansion of the Universe.
However, the siutation was very different in the earlier history of the Universe. Radiation energy density increases faster than the energy-equivalent density of matter as you go back in time in an expanding Universe (essentially because the energy of the photons also increases, while the mass of matter stays the same). So radiation dominates the early evolution of the Universe.
What are the steps that allow a conversion of 3 degrees K to 7.3 cm. =
wavelength and then to 4080mc/s? Also, what is mc/s?
Submitted by rsplan"AT"sbcglobal.net 11/02
There are similar questions answered elsewhere on this page. So let me give you a short reply.
The energy of a photon is Boltzmann's constant times temperature (actually the average is a numerical factor times that, since for a given temperature there are photons of a range of energies, distributed according to the blackbody spectrum). The energy of a photon is also Planck's constant times the frequency. Equating these means that you can convert a temperature into a frequency (and wavelength is then just the speed of light divided by the frequency).
All you have to do is look up Boltzmann's constant, Planck's constant and the speed of light in whatever units you want to use. I personally prefer to stick to SI units, but that's a matter of taste. I believe that "c/s" probably refers to "cycles per second", but I don't see how you can get near 7cm, since the CMB peaks at millimetres rather than centimetres. [Note added later: it has been pointed out to me by res04047"AT"verizon.net that these numbers probably come from Penzias and Wilson's original CMB measurement, which observed at a single frequency well below where the CMB spectrum peaks, namely about 4.1GHz or 7.3cm wavelength.]
If you want to be numerically accurate you also have to be careful to define exactly what you mean when you get a wavelength from the temperature. You'll get slightly different answers depending on whether you are thinking of the average photon energy, or about the peak of the spectrum measured in intensity per unit wavelength, and another answer for the peak measured in intensity per unit frequency.
Considering the CMB exists... is it possible to trace back and find the
spot in the universe where the big bang actually took place? Or would
this give a directionality to the universe, which it does or does not
have? Or ... is there a spot in the universe today where we can say the
initial event occured ?
Submitted by drogovitz"AT"cox.net 12/02
There is no centre of the Universe! Or, more accurately, everywhere is the centre! If you run the clock backwards in time, the Universe contracts, so that (at least in principle) everywhere was in the same place at the beginning.
The CMB photons are travelling in all directions from the material in the early Universe, and everyone detects the ones which are reaching them at the moment (by definition of course!). These come from all directions, and so contain no useful information about any part of the Universe being particularly special.
OK, you wondered if any interested surfers (i.e. Physics 11 only)
wanted to think of reasons why the temperature of CMB is -270.425° Celsius.
Did the frequency of the radiation just find a happy medium so to speak? An
equilibrium? [abridged]
Submitted by nutroman"AT"hotmail.com 12/02
Good idea! Except that the temperature of the CMB keeps dropping as the Universe expands. So there's no reason (as far as we know) why the CMB temperature should have its particular value that we measure today. It will keep continue to drop, so that, for example, when the Universe has expanded by another factor of 2, the CMB temperature will be half of what it is today.
How does a 3000 degree K gas have enough energy to keep hydrogen
and helium ionized? ... I get something like
32,000 degrees K to keep hydrogen ionized. [abridged]
Submitted by wrx"AT"mail.cruzio.com 12/02
This is a good question! If you go through the calculation you find that the temperature required to ionize hydrogen is at least an order of magnitude higher than that. But the ionization happens through interaction with the CMB, and there are about a billion photons per hydrogen atom! So this is very different from your mental image of heating up a box full of hydrogen atoms in the lab.
A more accurate calculation comes from estimating the temperature at which about a billionth of the photons have enough energy to ionize hydrogen. That obviously needs a temperature which is a lot lower, and much closer to the right answer.
To get precisely the correct value, you need to consider all the processes occurring between the levels in the hydrogen atom and the CMB photons. These calculations are very tedious (I know, since I've done some of them!), but give an answer which is about 40 times lower than you would have naively thought.
If you're really interested in some of the details you can read our short paper astro-ph/9909275. I won't even mention the longer paper!
Why are photons 'free' after recombination? Isn't the universe
still pretty dense? Is there some sort of 'electronic cross-section'
that makes ions fat targets for photons and neutral atoms 'invisible'?
Submitted by wrx"AT"mail.cruzio.com 12/02
Yes, that's pretty much right! Except that it's the free electrons that are the big cross-section targets for the CMB photons.
at the time of big-bang the matter and energy burst out from the
singularity simultaneously.Since the radiation has got the speed
of light,it might have passed the matter just after the big-bang
(matter cant travel as fast as light).then how we are able to
collect the radiation from all the direction-with almost same
intensity? [abridged]
Submitted by sreenath_sc"AT"rediffmail.com 2/03
The term "Big Bang" is considered inappropriate by many cosmologists, because it conjures up entirely the wrong picture of the first instants of the Universe. The "Big Bang" was not an explosion of the Universe into something, but an expansion of the whole of space. It's better to think of this happening everywhere at once, rather than at a point in space. That at least might help you sort out why there are CMB photons coming at us today from all directions.
My big problem with MBR are the words:
Afterglow, remnant,
and similar ones.
How can photons, traveling outwards from the big-bang
one millimeter center of explosion be seen today? [abridged]
Submitted by amrespi2000"AT"yahoo.es 2/03
You should see the rest of this page for more complete answers to this question. It is a very good question, and probably the most asked one about the CMB!
The short answer is that your pcture of the Big Bang being a localised explosion is wrong. The Big Bang happened everywhere at once in a Universe which is in principle infinite. So we see CMB photons as the "afterglow" of the early hot phase of distant parts of the Universe.
The real problem is with the terms "Big Bang" and "explosion", which should be removed from all descriptions of the early Universe!
[abridged] All the papers speak of photons as if they were "there",
waiting to be seen and cooling with the space dilatation. But
photons are not "there". They are travelling either
outwards or, if the universe is closed, along the
surface. The big problem is to explain what are we
seen when we see the MBR.
Submitted by amrespi2000"AT"yahoo.es 2/03
The idea is that photons are travelling at the speed of light from the early times when they were emitted (by the hot Universe then). The ones which we detect here and now were emitted billions of years ago, at positions which are billions of light years away from us. While they travelled through the expanding Universe they cooled, so that today they are detected as microwaves.
Like many other questions about the CMB photons, the trick is to get the right picture in your head, and then things should become much clearer. Don't picture the photons originating in a finite region within a much larger Universe. Instead imagine an arbitrarily large Universe, with the photons emitted from everywhere.
What I
don't understand is why we should still be seeing this radiation at all. It
should have left at the speed of light. Expansion of the universe
notwithstanding, shouldn't it have passed us up by now?
Submitted by Steven.Bailey"AT"bakerhughes.com 2/03
This is another example of essentially the same question that I feel like I've answered a million times before! Does anyone read any of these other answers?
I don't mean to suggest that this isn't a very good question. It may be that I just haven't yet come up with a devastatingly clear answer. I am convinced that the reason people ask this question is because they have the wrong picture in their head for what the Big Bang is about, and where the CMB photons come from (not from an isolated region in the early Universe anyway). However, I suspect that different people have slightly different ideas, and so it may be that no single answer will help everyone out.
I'd be interested to know which of the various responses on this page you might find the most helpful in answering variants of this question! I can post your reply here.
Some friends and I had discussed a question you addressed several times
in your FAQ. If Cosmic Background Radiation began at a point and was as
a relatively short flash of light, finite in duration, shouldn't there
be an end to the light we see now?
Submitted by lee"AT"mighdoll.net 3/03
It's nice to get someone e-mailing me an answer for a change! Here's the rest of this message, which is a pretty good explanation of why the CMB photons haven't all passed us by now:
"I think I get it now. The answer, as I understand it, is that the Universe was infinite in size when the flash went off."
"The point source is a misconception, confusing at best. The universe was once smaller, but we were always inside of it. Also, the radiation is now observed from all directions more or less equally, not from one direction as one might expect if our region of space was somehow to one side of the bang."
"As each region of the universe became transparent, the flash released from that region was indeed finite in duration. So when we look in one direction, we see a flash from a region that became transparent perhaps 13 billion hears ago. The flash we see from that region will in fact fade out. But just behind that region is a second region, and behind the second region is a third region, etc. And so if the Universe is infinite, we'll never run out cosmic background radiation."
You have answered the "why hasn't light passed us up already?" several
times. I think the problem is that many other sources (web pages and books)
say things like "when the universe was the size of a marble," etc. I did a
google search on the phrase "when the universe was the size" and got over a
hundred hits. I think all those pages would be more correct to say "when the
matter now visible was within a size of..." And I think your answer could
say that the CMBR we see today was outside of our observable universe
yesterday.
Submitted by rberger"AT"enercon.com 5/03
Excellent, thanks!
Let me just say that "the CMBR we see today was outside of our observable universe yesterday".
Essentially all of our information on the early Universe comes from the
cosmic microwave background. Why is this radiation so important for these
studies, and why can't we use other forms of information (or can we and
we just haven't done it yet)?
Submitted by gman_nda_gs300"AT"hotmail.com 2/03
The CMB anisotropies (temperature variations from place to place on the microwave sky) contain a great deal of information about out Universe, being basically a snap-shot of variations in density at a time of about 300,000 years after the Big Bang. There is really a lot of useful information to be mined from the CMB, but that doesn't mean there aren't other ways to probe the early Universe.
One example is that the spectrum of the CMB should contain small deviations (so far undetected) which also give us information on times going back to about 1 year. The abundance of the light elements tells us about conditions in the Universe after only about a few minutes. The fact that the Universe contains a preference for matter over anti-matter might tell us about high energy physics at much earlier times. As well as the CMB, clustering of galaxies and other objects can tell us about the types of density variations which existed in the very early Universe. There is some real hope that their may be information there about times as far back as 10-30 or so seconds!
Does the CMB appear as a hollow 'sphere' around our entire universe? As
if our universe is inside this hollow sphere.
Or is it everywhere, like water in a fish tank?
With our universe as a fish in the tank, And the water is the CMB?
Submitted by ABRAMS1117"AT"webtv.net 3/03
The situation is more like the second picture. However, I'm afraid to have to tell you that both sound incorrect to me!
Our Universe is the whole of this sea, and not something embedded in it. You need to (somehow) imagine an infinite ocean, filled with the CMB photons, which were generated everywhere in the ocean at some early time. The Earth is one miniscule little shrimp in this vast ocean. We can only see a finite volume, since the ocean has only existed for a finite time, and light travels at a finite speed. But the entire ocean is so big that we may as well consider it to be infinite.
Is there any thing original to be done on CMB yet? I couldn't find a good
topic for my research. [abridged]
Submitted by alencar"AT"ccard.com.br 3/03
That's a good question! Many theorists working on the CMB (myself included) are searching for things to work out which fulfill the following criteria: (1) not already done fully; (2) worthwhile to calculate; and (3) not too difficult!
I have some ideas of my own, but of course I'm not going to tell you what they are!
But seriously, there is still a great deal to be worked out involving the "higher order" effects in the CMB. There are many weak effects of the formation of structure on the CMB, only some of which have been worked out in detail. These involve things like lensing, reionization, galaxy clusters, statistics of the anisotropies, etc. And there are no doubt things like these that we haven't even thought of yet. Good luck!
I keep reading and hearing about the CBR "cooling" to its present
microwave frequency, but what does this mean? Cooling usually
involves a flow of energy to something or somewhere else or a
change of energy to another form (e.g. kinetic to gravitional). As
I understand it the CBR photons have not interacted with anything
else since they were emitted, but their wavelength has been
stretched because of the expansion of spacetime, so their frequency
has reduced. So what has happened to the photons' original energy (h times
frequency)? Has the conservation of energy been violated? Where
did the energy go? (abridged)
Submitted by ianw"AT"netspace.net.au 3/03
This a good question, which is often asked. Let me try to answer it a slightly different way.
All expanding gases lose energy. This is sometimes called "Joule-Kelvin" expansion. Basically, the expanding gas does work, through its pressure acting to change the volume. The energy lost by the gas is exactly equal to the work done in the expansion.
In the cosmological context you can think of the CMB as a gas of photons. This is a relativistic gas, with a different relationship between pressure and volume than the more normal "ideal gas" that people are more used to thinking about. But the principles are the same, and energy is conserved for exactly the same reason. The energy lost by the photons goes into the expansion.
I do not see how the Joule-Kelvin effect is related to
the CBR. Wouldn't a photon gas be close to perfect?
I believe there is no attractive force between photons
(other than gravity) and they have no significant size, so
they are not like a van der Waal gas. Is the expansion of
the Universe and CBR perhaps more like the free
expansion (Joule effect) case?
Do the CBR photons perhaps lose energy to self-gravity
over eons of time and space, like the reverse of a gas
cloud condensing into a star and heating up as the
molecules lose gravitational potential energy? If not,
what IS the mechanism by which the photons lose energy
and lower their frequency?
(abridged)
Submitted by ianw"AT"netspace.net.au 4/03
OK, I can see I'm going to have to be more hard-core about my answer here!
The bottom-line is that within the context of the solutions of General Relativity which apply to a smooth expanding Universe, there is local conservation of energy. For any finite volume the energy lost by the photon gas is equal to the "PdV" work of the expansion. Stating that this is like Joule-Kelvin expansion is just an analogy.
There are of course many ways to think about this. In one picture you just imagine that the photons are redshifted by the expansion velocity. So if that helps you, then there's the explanation! However, this isn't really the case in an expanding Universe in General (rather than Special) Relativity. It's better to think of redshift as being caused by the changing scale factor, i.e. photons have longer observed wavelengths than they had when they were emitted because the Universe has been expanding while they travelled towards us.
It's true that normally you would like to think about the physical interactions which change the photon energies. But this isn't a normal everyday situation we're talking about here! The decrease in energy of the photons has nothing to do with interactions with matter, or virtual particles, or even the Doppler effect. It is really a consequence of General Relativity. Photons travelling through an expanding Universe lose energy on their journey between emitter and receiver, without interacting with anything.
(3^3*2^8*pi^3/a^7)^1/2*Qo*([1N]*G/c^4)^1/2*[mol]*NA/N^3)=2.7111K
The formula is only a conjecture! But:
There is a contribution from the free electron to the CMB and so to the
temperature. Tb=2.73K
Possible?
As well as from other "particles" (universe, electron, hydrogen atom
...)
(Qo is the Planck temperature and NA Avogadro's number. N=integer about
1e22 reflects the restmass of the electron.)
Submitted by manfred.geilhaupt"AT"fh-niederrhein.de 4/03
Good effort at CMB temperature numerology! However, I'm not sure this is dimensionally correct! And I think that dividing by 10^22 arbitrarily is against the rules! You can see my own attempts at this on my "Who Chose the Temperature?" page.
Since no one knows what the emission spectrum of the spontaneous creation of
sub-atomic particles in space would be, isn't it somewhat possible that
that's where the CMB comes from?
Submitted by Beanstalkr"AT"aol.com 3/03
I'm not sure what exactly you mean by "the spontaneous creation of sub-atomic particles in space", but if you're talking about a "Steady State/ Continuous Creation" sort of picture, then there are many reasons why this doesn't work. Not least of which is the need to explain the power spectrum of CMB anisotropies, which is a stunning confirmation of the standard hot early Universe picture.
But just as there's some truth in the Steady State model (since it's quite like inflation in many ways), there's something in what you say. In the standard cosmological picture the Universe used to be very much hotter and denser, and at early enough times was filled with particle/anti-particle pairs in equilibrium with the radiation. As the Universe cooled most of these annihilated, adding to the photon background. So you can say that most of the CMB photons had their origin in the spontaneous destruction of matter!
if the CMB is cooled by the expansion of the
universe, would it not be possible to measure it's temperature very
accurately and determine the rate of cooling? [abridged]
Submitted by thxgoon"AT"hotmail.com 4/03
In principle you could certainly do this. Let's imagine you measured the temperature of the CMB today and then waited 10 years and measured it again. Then of course it will be a bit cooler. But by how much? Well the CMB is redshifted by the expansion of the Universe, and the expansion rate is given by the Hubble constant. The Hubble constant is measured to be about 70 km/s/Mpc (kilometres per second per Megaparsec). The Hubble time (one over H0 in time units) is about 14 billion years. So in 10 years the CMB temperature will have changed by only about one part in a billion! That's pretty hard to measure, and so this method isn't going to be a way to estimate the expansion rate of the Universe.
If the CMB really exists, and
therefore the big bang is right and there is no god, why can't I just hold
my food (e.g. burritos) up in the air to cook them? Why aren't I getting
cooked as we speak.
Submitted by ilovecosmology"AT"hotmail.com 4/03
Cosmic microwaves fill the entire Universe. However they're extremely dilute by terrestrial standards. CMB radiation at 2.725 Kelvin corresponds to a flux of approximately 3 × 10-6 Watts per square metre. So the energy passing through a burrito (depending on how big the burrito is) must be around 10-7 Watts. On the other hand your microwave oven is an efficient way of converting hundreds of Watts of power into microwaves and directing them at your food. In addition microwave ovens tune their radiation to zap the molecules in your food, whereas the CMB covers a wide range of frequencies.
So you can't cook your food by holding it up in the CMB I'm afraid. I have no opinion on whether or not this proves the non-existence of God though!
Here's a good site which is like the microwave ovens version of this one: Microwave Ovens
Does CMB affect us today at all? If yes, how so?
Submitted by orem2"AT"TCNJ.EDU 4/03
No, it doesn't.
The CMB is completely useless. There are no direct applications that I know about, either beneficial or harmful.
Except of course that the anisotropies give us a way of determining exactly what sort of Universe we live in. One of the definitions of Civilisation is a society which places a value on certain things simply for their interest, rather than simply valuing utility. The CMB fits firmly into that category. We stufy it "merely" because understanding the entire Universe is pretty interesting!
If you could please tell me the frequency of the CMB.
I think there is a frequency give or take.
I'm not concerned with 1/100,000 deviations from average. I just want
the average.
Submitted by nikrubenstein"AT"hotmail.com 4/03
The CMB is "blackbody radiation" meaning that it is the sort of radition you get from a hot body which has settled down to be at a particular temperature. The energy is spread over a wide range of wavelengths, and the shape of this energy spectrum is described by a specific mathematical formula, which rises as a power of frequency and falls of exponentially at higher frequencies. The spectrum peaks around a frequency of 300GHz, but it's important to realise that the photons have a spread of frequencies around this value, and CMB photons can be detected from hundreds of MHz up to hundreds of GHz.
I got to wondering -- how bright would the night sky be if we could see the micr
owave background? Compared, say, to moonlight?
Submitted by res04047"AT"verizon.net 5/03
The answer depends on what units you use.
In terms of energy flux, the CMB is fairly similar to starlight within our Galaxy. So if you could see it, and your eyes detected energy flux, then it would be a uniform glow, with individual stars visible on top of it, and the Sun of course very much brighter.
If, on the other hand, you detected number of photons per unit time, then there are a lot more of those than from starlight, and so the CMB would dominate.
You could also easily imagine other sorts of detectors, which effectively work with different units, and would give different answers.
Who discovered the Cosmic Microwave background?
Submitted by asim_48"AT"yahoo.com 7/03
The Cosmic Microwave Background was discovered by Arno Penzias and Robert Wilson sometime in 1964 during studies they had been making using a sensitive microwave receiving system at Bell Labs. The results were published in 1965 and the pair received the Nobel Prize in Physics for their discovery in 1978.
Given that all of space expands at the
same rate...then spaces that are farther apart from one another expand away
from each other faster than spaces that are closer together ...
At what distance between points would space expand faster than the speed of
light? ...
Given the tiny amount of radiation energy that can theoretically emit from
black holes as virtual pairs of matter/antimatter as one part of the pair is
ejected past the event Horizon, and the other out into space ...
Could this show up as a constant background radiation that could be detected
from any portion of the sky? [abridged]
Submitted by jjrittenhouse"AT"hotmail.com 7/03
This is a very nice question! And a proper answer would, I fear, be quite long!
Let me say a few short things in response. Firstly, this is not a good explanation for the origin of the CMB in any model that I'm aware of. Seondly, parts of the Universe certainly can expand away from each other faster than the speed of light. And thirdly, your description <>does bear some striking similarities to a picture of how fluctuations are made during a period of inflation - you can kind of think of this as like a temperature that empty space has as a consequence of accelerating, then that temperature is manifested in fluctuations in the relevant fields at the inflationary epoch, which later become the fluctuations in density, which even later get imprinted at last scattering as the CMB anisotropies.
someone is asking me the order of magnitude of the number of real photons there
are per meter cube in the CMB. do you have the answer ready or can i work it
out from N = sigma T**4/chv where hv is the photon energy at the max of the
black body law for T about 3K ?
Submitted by 7lucas"AT"fundp.ac.be 8/03
You can get a rough answer from the formula that you wrote down, which will be off by some small factor (depending what you use for the average frequency). The correct answer simply comes from integrating over the blackbody function. The value obtained is about 411 CMB photons per cubic centimetre.
I am confused about the time and distance scales. The wavelength of the
CMD is about 1000 times longer than that emitted by a black body at
3,000 K. That part is clear. When I divide the age of the universe, 15
billion years (to use a round number) by the age at last-scattering
(300,000 years, the oft quoted number), I get a factor of 50,000. How
can the universe be 50,000 times older than it was at time of last
scattering, but only 1,000 times larger?
Submitted by pbwilson"AT"cox.net 8/03
I'm always happy to get questions which show that people have been thinking!
The answer to your quandary is that the stretching of lengths in the expanding Universe is not at the speed of light. In other words the evolution of the "scale factor" is not proportional to time. This is because of the matter in the Universe which causes deceleration (at least until fairly recent times when it appears the Dark Energy causes it to accelerate). It turns out that for most of the history between now and last scattering (when the CMB photons had their anisotropies imprinted) the scale factor evolved as roughly the 2/3 power of time. So the age ratio is expected to be about the scale factor ratio to the 3/2 power. That's much nearer to the numbers that you were stating. Although to do it properly one needs to solve the detailed equations, taking into account the accelerating phase etc.
The recent results from the WMAP probe included a very precise estimate of
the age of the Universe of 13.7 +/- 0.2 billion years. I have yet to find a
good explanation for how the age of the Universe is derived from the cosmic
background radiation patterns that were recorded by WMAP.
Submitted by djalbright"AT"generatortech.com 10/03
The WMAP satellite precisely measured theanisotropies over a wide range of angular scales. The way that the amplitudes of the anisotropies vary with angular scale can be fitted using cosmological models. The anisotropies are accurately fit using a model which has come to be known as the "standard cosmological model", with well determined values of its parameters. This model has close to flat geometry, and is dominated by dark energy, with about one third of the Universe's energy density in dark matter and about 4 per cent in ordinary matter. It is expanding at a particular rate, measured to an accuracy of better than 10 per cent, and it contains fluctuations of the sort produced in "inflationary" models of the very early Universe. The age of the Universe is a derived parameter within these models, but it turns out to be quite robust. If you restrict the range of models to just those which have exactly flat geometry, then you get the number you quoted. If you allow more freedom in the models, then you always get pretty much the same number, but with larger undertainty.
You write we see microwave radiation from the last scattering. Let me suppose
we are in the Milky Way and we are looking into the last scattering
surface A across the sky. "A" was the scattering object farther away 1 million
years after BB from the precursor of the Milky Way. 1 million years after the
BigBang Milky Way and "A" were X light years apart. At that moment radiation
came out of A towards Milky Way. Should it not have gone by by now? How can we
still see it?
Submitted by tierrasana33"AT"netscape.net 10/03
This is another example of the most asked question about the CMB! "How come the photons haven't already passed us?" has been answered on these pages several times before.
Let me add to this question that if we see "A" in CMB photons today, then it must be the right distance from us so that light would take basically the age of the Universe to travel between us. So the distance "X" is whatever it has to be for us to be receiving the early Universe photons today. For objects closer than this, we are seeing the CMB photons coming from behind them, also distance "X" away.
Right now it is at 2.73 Kelvin. Is it getting cooler?
Why do I ask? Because a Stanford PHD student described some work they
were doing with extremely low temperatures in the range of .5 Kelvin. He
claimed
that light sent into chambers at this temperature actually slowed down ...
can we look forward to a time in the (far distant) future when the CMB reaches
.5 Kelvin and the light between the galaxies actually slows down? [abridged]
Submitted by Michael.bechler"AT"Eclipsys.com 11/03
Yes, the CMB temperature is decreasing, but it takes a cosmologically long time for it to change by much. Basically it takes about the Hubble time to change by order unity, in other words you'd have to wait millions of years to see a change which is very noticeable.
I'm not familiar wth the slow-down effects you describe, but it surely must involve matter at fairly high densities. The speed of light in a vacuum is always, well, the speed of light! It's slower through material, and presumably these people have been investigating some effect where it slows further in matter approaching zero Kelvin. But in the average part of the Universe the density is so extremely low that all such effects will be negligible.
I am just wondering if CMB radiation could be used to determine the outline
of a blackhole? Does CMB radiation accumulate in huge quantities within the
vicinity of steep gravitational wells? In short, What is the effect of
Blackholes on the CMB radiation?
Submitted by Michael.bechler"AT"Eclipsys.com 11/03
This is a nice question!
The answer depends on whether you are asking a practical question, or a point of principle.
Practically speaking, the size of a black hole is so small, and they are so far away, that it will surely be next to impossible ever to measure any effects. It is made even harder by the fact that black holes are typically surrounded by accretion disks and other hot matter, which will have a big effect at the wavelengths you'd observe the CMB. In any case, there are way easier ways of detecting black holes!
The question of principle is slightly complicated. The effect will be mainly the gravitational lensing of the CMB by the black hole. But, since this just moves light around, and the CMB is pretty darn uniform, you wouldn't really see any difference! However, you would have an effect on the CMB anisotropies, and this is potentially measureable, just as the lensing effects of galaxy clusters are measureable in the near future (e.g. by the Planck satellite).
I was wondering if you knew how the spectrum Cosmic Microwave Background
supported the idea that the Universe expanded from it's inital hot state.
Submitted by sogus"AT"email.arizona.edu 11/03
Yes, I do know that!
But presumably you also would like me to tell you the answer, right?
The spectrum is such a good blackbody, that no one has a good idea how to make it except from a hot early phase of the Universe. The "Big Bang" model naturally makes a hot blackbody spectrum early on, and then it just gets redshifted to the present, retaining its shape, but cooling.
Somebody wrote that "most of the entropy of the universe is found in the
CMBR"..please explain further. What is Entropy by the way? Is it something
tangible, something that could be felt? A force? or a form of Energy?. Could
it counter Gravity and Time Reversal?
Submitted by fidel_mc"AT"hotmail.com 12/03
Good question!
The answer to the last part is "no". Entropy isn't nearly so mysterious. It's a quantity which describes the degree of disorder in a system. It is a quantity which cannot decrease for a closed system, and which is often constant if physical processes are very slow. For much of the history of the Universe the entropy per unit volume has been constant (provided you take account of the expansion of the Universe).
For a uniform "gas" of particles the amount of entropy can be calculated, and depends on the energy, pressure and temperature. For a gas of normal matter particles the entropy is proportional to the number of particles, N, multiplied by (m c2/kT), where m is the particle mass, c is the speed of light, k is Boltzmann's constant and T is the temperature. However, for a "gas" of photons (or other highly relativistic particles) the entropy is just proportional to N. Since there are a lot of CMB photons, then their entropy density dominates the entropy of the Universe.
When will the photons in this frequency range stop coming? In other
words will there ever be a time when no more CMB will be detected?
Submitted by retep29805"AT"netzero.com 12/03
As far as we know the CMB photons will keep coming forever!
However, they will continue to redshift, so that billions of years in the future most of them will be at longer wavelengths. Our far-distant descendents will presumably talk about the "Cosmic Radio Background"!
... I am having some
difficulty coming to terms with the notion that if the CMB is 15 billion
years out, that the big bang is only +300,000 years beyond it, in a
universe that is spacially very small...
So how is it that after 15 billion years we are being bombarded by big bang
radiation on all directions that should have by now accelerated past us,
since we are matter originating frrom the same event? [abridged]
Submitted by gterry"AT"au1.ibm.com 12/03
This is, I believe, another example of the "why haven't the CMB photons past us" question. I suggest reading the answers to other similar questions on this page, to see if that helps.
A short answer might be that you should think of the early Universe being very large. The CMB is simply the photons we see coming from a sphere around us of size equal to the light travel time in the age of the Universe (or minus that 300,000 years if you like). It might help to think about sound waves coming at you from a huge crowd of people who all shouted something at once - at any given time you hear the sound from a circle of people around you, with the radius being the sound travel distance since the time of the Big Shout.
Suppose I had the technical means to manuever myself so I was in the CMB
reference frame: Would I then be unable to decect any photons from the CMB?
Submitted by rich"AT"concordma.com 12/03
No. You would still detect the CMB, but it wouldn't have a dipole pattern. In other words, you'd get the same flux of photons in every direction. Since we're actually not in this frame, but moving at a few hundred kilometres per second with respect to it, we see about 0.1% more photons coming from one side of the sky (the side we're moving towards) and the same amplitude of deficit from the opposite side. This is what we call the "CMB dipole", and we can use it to measure our speed through space.
In case there's a confusion here, being "in the CMB reference frame" means nothing more nor less than being in the frame of reference in which there is no dipole. It doesn't mean moving at the speed of light along with the CMB photons. They are coming at us from all directions, and hence there is no frame of reference in which they are all at rest, even if we could travel at the speed of light.
If this radiation is mainly photons, whay is it still visible, rather than
having radiated out of sight, range and mind about 12 billion years ago?
Why is it still visible equally (with local variations) in all directions?
Submitted by Anjodon"AT"aol.com 01/04
Because it comes from the whole Universe! You can read several different answers to this (or essentially this) question elsewhere on this page.
Here's an analogy which might help. Imagine you are at a very important sports event, with an enormous crowd. So enormous in fact, that it takes a significant amount of time for sound to travel from one side of the crowd to the other. Let us say that you are somewhere in the middle of the crowd, so we don't have to worry about any edges etc. And imagine that at some particular instant there is a crucial point scored in the game. Everyone in the crowd lets out a loud shout at the same time (they are all watching the game with basically no time delay, since the speed of light is so fast, in case you were worried about that complication!). Now the question is, if you wait until, say, 13.5 seconds later, which people are you hearing the shout from?
The answer is that there is a circle of people around you, each located 13.5 "sound seconds" away from you (i.e. the distance sound travels in 13.5 seconds). The shouts from the closer people have passed you already. The shouts from the more distant people haven't reached you yet (this requires that the size of the crowd is several kilometres across, but never mind that!). If you wait a little bit longer you will be hearing the shout from the people who are 13.6 "sound seconds" away, etc. And if the crowd is big enough, then there will always be people sufficiently far away from you that you will be hearing their shouts at later and later times, from more and more distant circles centred on you. And some friend of yours located at some other position in the crowd will also hear the shout from a 13.5 "sound second" radius circle, but their circle will be different from yours.
The arrival of the CMB photons is exactly like this! Except that we live in a 3 dimensional Universe, rather than a 2 dimensional ceowd of people, and that the CMB photons travel at the speed of light, rather than the speed of sound (about 1,000,000 times slower). At some epoch in the early Universe, everywhere emitted CMB photons. About 13.5 billion years later we are now seeing the photons arriving at us from a sphere of radius 13.5 billion light years. 100 million years from now we'll be seeing the photons from parts of the Universe which are 13.6 billion light years away, etc. So the photons did not pass us all already, because they come from everywhere - just like shouts from a huge crowd of people.
Although CMB which we observe _locally_ have T=2.7,
CMB which was generated here 13 billon years ago
does _not_ have T=2.7 _in our frame of reference_.
It is flying some 13 billion light years away
from us now with v=c but it is still gamma rays!
So, E = (energy density) x (volume of sphere)
isn't ok - energy density is not constant
(again, _in our frame of reference_)
Do I miss something here?
[abridged]
Submitted by vda"AT"port.imtp.ilyichevsk.odessa.ua 01/04
The CMB photons are travelling at the speed of light in all directions, and hence the ones we see in some direction today came from over there a long time ago! But an observer in that location today will be seeing our CMB photons now. There has been a factor of 1000 in redshift between the CMB "last scattering surface" and today, and hence the photons have had their wavelengths shifted by that factor. That means that the photons leaving our last scattering surface were roughly 1 micron in wavelength at that epoch, and redshift to roughly 1 mm wavelength on their way to us. At that same original epoch our region of the Universe was full of roughly 1 micron photons too, and those photons propagated in every direction, and today are reaching distant observers (at the location of our last-scattering surface, but at today's epoch), who would detect them with a wavelength of about 1 mm too.
According to the expanding Universe picture, the Universe really was hotter in the past, with temperature simply inversely proportional to (1+redshift) [here I'm using redshift as a label for the time coordinate, higher redshifts mean earlier times].
If we want to estimate the total energy in the CMB in some volume at the present epoch, then we just take today's CMB density and multiply by volume. There's no redshifting in this calculation, since we're assuming we can do the calculation at a single time. Of course you could also ask about the integrated density along a coordinate where time changes proportional to distance (technically called the "light-cone"), but that would be a different question.
What is responsible for the "background" aspect of CMB. We speak of
"background noise" and understand it as composed of emitted and
reflected noise in an echoic environment. Since all the original
radiation that makes up the CMB was emitted over the relatively short
period of time of plasma coalescence about 380,000 years after the big
bang and streamed away in all directions at the speed of light, with all
the matter formed during the coalescence following behind at less than
the speed of light, how can we be bathed in this radiation today? What
is the mechanism by which it is reflected or refracted or absorbed and
re-emitted back to us today? What causes the echo?
Submitted by ogdennr"AT"laplaza.org 01/04
This is a somewhat more sophisticated version of the "why haven't the CMB photons passed us already" question, which I've answered many times before!
One thing to understand is that everywhere in the early Universe was emitting photons, not just some finite region. So there is no reflection, refraction or absorption - the photons simply stream straight towards us from wherever they originated. For us this is a spherical shell the distance away that light has travelled since the Universe went neutral about 400,000 years after the Big Bang.
[abridged]
I am wondering if you might be able to steer me in the direction
of some other very easily read information regarding the CMB, other than
your wonderful site of course.
Submitted by christopherrobincox"AT"peoplepc.com 02/04
Although obviously nothing compares to this site, you might want to check out one of these: Wayne Hu's introdution to the CMB; WMAP's overview of the CMB (and you could look at other things there too).
Is the CMB red-shifted, and if so, how much?
Submitted by JCEvans"AT"hntb.com 03/04
Yes, the CMB is very much redshifted!
The photons which make up the CMB were created in the hot early Universe, and have been decreasing in energy as the Universe expands and cools. We see the imprint of the anisotropies caused when they last interacted with matter at a redshift of around 1000. But the photons themselves were created when the Universe was hot enough to make lots of particle/anti-particle pairs, at redshifts of billions.
So you can think of the CMB photons being created as high energy gamma-rays when the Universe was billions of Kelvin. They've had their wavelengths stretched by a factor of something like a billion so that today they represent radiation with a temperature of only a few Kelvins.
hey, you guys dont no if thats the edge of the universe or that
the cosmic backround just isnt some big line around a huge group of galaxies
that we are inside kind of like the thing that gois around the solar
system , i bet there are a shit load of bubbled in mass amounts of
galaxies and star things that were in, i cant stand that you guyts
actually think that the universe is finte thats rediciluous. First of
all you can only say wat you telescopes can see and defently you guys
cant see infinte space so dont bother with that cbm stuff its ridicilous.
Submitted by blizzard710"AT"hotmail.com 03/04
That's an interesting point of view, which I thought I'd share with everyone in its entirety.
Actually my own hunch is that the Universe is infinite in size. Or at least half that big anyway.
I read somewhere that at the point of last
scattering, the CMB (although not in microwave form) was some 3000
degrees Kelvin. If this is so and it is now cooled to 2.73 degrees
Kelvin by the effects of universal expansion as the universe becomes
less dense, by my estimates of averages, in about 12 to 13 million years
the average temperature will reach zero Kelvin, or absolute zero and
will no longer be detectable. Is this a correct assumption?
Submitted by grojo"AT"elpn.com 04/04
The CMB is getting cooler all the time, in direct proportion to the expansion of the Universe. The more the Universe expands, the colder it will get. But it won't ever get to zero, although you can imagine it being arbitrarily small by going further and further into the future.
In a Universe dominated by Dark Energy (currently the best guess picture), the expansion is becoming exponential. The expansion rate (otherwise known as the Hubble parameter) becomes constant, and we're almost in that situation already. Assuming exponential expansion with the exponent measured in Hubble times (about 1010 years), then the sums are relatively easy to do. You need to wait about 10 billion years before the temperature has fallen to about 1 Kelvin. And in 12 million years the temperature has only changed by only about a thousandth of a Kelvin.
You state in some of your answers that we can only observe CMB photons
which could have traveled this far at the speed of light since the last
scattering; implying, to me anyway, that there would be something beyond
that horizon. If there is indeed something beyond that horizon
(possibly a lot), doesn't that mean that the universe is older than the
estimates, since those estimates must be based on what is observable?
If I'm not way off base with my reasoning and the models have not
already accounted for this, what are the implications of an older and
larger universe?
Submitted by JCEvans"AT"hntb.com 05/04
There is certainly stuff beyond the "last scattering surface", although we can't directly see back then using CMB anisotropies. But we can probe those distances (and times, since looking out further and further means looking back further and further in time) using other probes of the early Universe (such as details of the formation of the light elements).
However, the best picture we have of the Universe puts the present age at about 13.5 billion years, but the age at "last scattering" at only about 300,000 years. So there really isn't very much further back that you can go! In other words the photons reaching us from the "last scattering surface" left on their journey not very long after the Big Bang (at least by cosmological timescale standards!).
The actual "particle horizon" is the distance beyond which we can't see because there hasn't been enough time for light signals to reach us from there. That's about 13.5 billion light years away (or actually a bit further because of the expansion of the Universe in that time). And of course there's lots more Universe beyond that, it's just that we won't be able (even in principle) to find out about it till later!
I enjoyed your tutorial in ISM and the mechanics of how the CMB may have
been emitted. Could you give me a flavor (or a good reference) that goes
into the theory of how the photons of the CMB were cooled, from the
presumably very high temperatures at which their emissions occurred, down to
the 2.7 deg Kelvin level. I would like to be able to develop a notion for
the energy loss/frequency shifting mechanism such as adiabatic expansion,
tired light, or whatever caused the centroid of the CMB spectrum to decline
(or if my conception is wrong, to start off so cool at the time of
emission).
Submitted by WHeller"AT"fdic.gov 05/04
It's really very simple to understand the idea. It's just that the Universe is expanding, and as the photons travel through space they have their wavelengths stretched along with the expansion. So all the photons produced in the early Universe get shifted to longer wavelengths as time goes on. This means that their energies are reduced (since the energy of a photon is inversely proportional to its wavelength). And hence an initially hot spectrum of photons looks just like a lower and lower temperature spectrum as the expanding Universe gets older. If the Universe was contracting, then the CMB would be heating up and would eventually cook us (but don't worry, that won't happen!).
the wave-length of CBR is constantly changing as the universe expands because
the CBR is expanding along with the universe. If we could note a change in the
wave-length of CBR, it would give insight into the rate of the expansion of
the universe. Is this right? If the rate of the expansion of the universe
is known based on Hubble's constant, how long should it be before we notice
a change in the wave-length of CBR?
Submitted by timothy.patry"AT"us.army.mil 07/04
Good question!
You're right that the CMB photons are being stretched all the time. Or another way to think about it is that the blackbody radiation is cooling, and so its temperature is decreasing. Unfortunately it takes a timescale of order the age of the Universe for the temperature to change by a substantial amount! You'd need to measure the temperature to about 1 part in 108 in order to see the difference over a human lifetime!
I would like to know if anyone has
looked for coherent electromagnetic radiation in
the radio frequency range - could
there be another type of CMB out there?
Submitted by alistair"AT"goforit64.fsnet.co.uk 07/04
I confess that I'm not really sure what this question means, sorry!
By "coherent electromagnetic radiation" I normally think about lasers and masers. Well you can certainly get such radiation in the microwave part of the spectrum, and there are even astronomical sources known to be masing. However, the CMB radiation comes from everywhere, and I'm not even sure how to talk about the idea of "coherent" waves coming from all around me. But I think the answer is that if the radiation was "laser-like" we would have known about it in about 1965. There could of course be "masing spots" coming at us from the microwave sky, but the only such sources we know about are very much local and not "cosmic background".
Our detectors see a steady stream of CMB photons raining down from all
directions. As I understand
it, these photons originated at a specific time (BB + 380kyr) at every point
in the expanding
universe. Like most people, I am tempted to ask where the photons we see NOW
have been all this
time. However, am I right in saying that we are seeing the event run over and
over, like a
continuous film loop in the sky? Did the photons we see at each second start
off in a shell one light-second further away?
Submitted by Sturandall"AT"btinternet.com 07/04
I think you're more or less on the right track here (although I'm not sure about the continuous film loop analogy).
Try thinking about the photons arriving here and now from all directions. A second ago they formed a spherical shell around us, one light second in radius, and all moving radially inwards. A second before that, they were in a shell 2 light seconds in radius, etc. So the photons arriving at us now used to be somewhere else and on their way here.
Once particular photons have passed us they'll never be back! But there's no need to worry, because there are always plenty more photons out there!
Last night I read ALL of your email answers to CMB questions.
I admire your skill and find your patience wonderful (even not minding
answering the same question more than once!)
The bits I have the most trouble with are
(1) "Space" - what IS it. How can it "expand". How can an "infinite"
thing expand?
(2) The radiation is downshifted "because the space it is in has got
bigger" - by which you seem to mean "THINGS in it have now got more
space between them"
Submitted by johnfree"AT"uk2.net 09/04
Firstly, let me congratulate you on reading all these FAQs - that must have taken quite a while! Then let me try to give some kind of answer to your questions.
For the first question, "What is Space?", that's really a very good one! There are probably several joke answers to this, and several clever-sounding philosophical answers that don't really help. The dictionary definition "that which makes extended objects conceivable and possible" is probably about the best you can do for an answer. Within General Relativity (our currently best idea for a theory of gravity and motion) you can think of space as a "field", in a similar way (although with different properties) to the electromagnetic field.
In a sense the reason that it can expand is because there are solutions of General Relativity in which it can expand! But that's really not a very satisfying answer. Some people like to think of the expansion of the Universe as the space between galaxies expanding, while other people like to think of it simply as the distances between galaxies getting bigger, and a third set of people can't see why the first two ideas are different!
Having failed to give you much of an answer for your first question, let me do an equally poor job on the second one! The radiation in the Universe is in a sense doing the "work" which makes the Universe expand. And objects in the Universe don't absorb all the radiation because there hasn't been enough time for that to happen. In other words the typical CMB photon can travel all the way to us from the early Universe without much chance of interacting with anything along the way. So the CMB photons continue to stretch as the Universe expands, and they don't get absorbed by the matter.
You wrote:
"The CMB photons we see today are coming to us from way across the Universe
(about 13 billion light years away, if for example the Universe is 13 billion
years old)."
Why do 13 billion yr old photons designate points in space 13 bly away?
Submitted by dreeves"AT"brandeis.edu 09/04
The photons don't choose us, we choose the photons!
The photons that we are observing right now must have come from a sphere around us which is (say) 13 billion light years in radius. There's nothing otherwise special about those photons. They "chose" to be observed by us now only in the sense that their neighbouring photons back then "chose" to be observed today by cosmic neighbours of ours.
Is it true then that the CMB wasn't always microwave? That it is microwave
now based on the degree of cooling the universe is at right now? That
previously the cosmic background (CB) was on the higher-energy end of the
spectrum, and that as time goes on and the universe continues to cool, the
CB will continue to migrate toward lower and lower energy regions of the EM
spectrum?
Submitted by hkc1"AT"tof-one.org 09/04
Yes! Yes! And yes!
(Those sure were easy questions to answer!)
Isn't it possible then that the CMB could essentially be a
manifestation of the "fabric" of space-time...the thing for which Einstein
mathematically "nails down" its behavior in general relativity? And if so,
is it not possible that certain fundamental "constants" that govern the
physics of our day could actually be slowly changing as the fabric of the
universe expands and cools?
Submitted by hkc1"AT"tof-one.org 11/04
No!
But actually these are harder questions to answer!
For the first question, I think you are asking whether the CMB can be the Dark Energy, or cosmological constant introduced by Einstein. That's not possible, since they behave in fundamentally different ways. The CMB is radiation, while the Dark Energy is "vacuum energy" (or something only subtly different from that in some models). These two substances have quite different relationships between their energy density and their pressure, which leads them to evolve quite differently in an expanding universe.
As for fundamental constants changing in time, this is certainly possible in principle. However, you have to be careful about what you mean by a constant, which is related to measurement and units. It's only really meaningful to talk about the variation of "dimensionless" quantities, or in other words ratios of fundamental constants. There are some claims that such a variation may have been seen by looking at spectral lines over a wide range of redshifts, but most cosmologists remain skeptical of these results, since the systematic uncertainties are hard to assess. There are also models in which the constants might vary in an observable way, but again, most cosmologists don't regard any of these models as particularly appealing right now.
I do not quite understand why the CMB is a prefect blackbody. How could
the... freeze out at recombination/decoupling not release a... distorted
signal since the Last Scattering Surface would still have a distribution
of photon energies even at 3000 K? Also, wouldn't this also result in H
absorption lines?
Submitted by lucero"AT"chem.ucla.edu 11/04
A "blackbody" is just the equilibrium distribution of photon energies for a given temperature. Back at the time of recombination the CMB was in vey good thermal equilbrium and therefore was very close to having a blackbody spectrum. This means that there was indeed a distribution of photon energies - just the right distribution to be a blackbody spectrum.
As for the second part of your question: there wouldn't be hydrogen absorption lines, since the amount of absorption is quite negligible. However, there will be a set of emission lines coming from all the hydrogen that went from ionized to neutral at the recombination epoch. These lines are incredibly weak however - remember that there's about a billion CMB photons for every atom in the Universe, and so there's about a billion times less of these line photons than general CMB photons.
I guess I just don't understand why it is still all around when there is =
no source for the radiation. Doesn't it travel?
Submitted by lucero"AT"chem.ucla.edu 11/04
There certainly is a source for the CMB. It's the entire early Universe! And the photons travel at the speed of light from where they were made until they reach us, about 13 billion years later. The Universe is much bigger than 13 billion light years, and all of it made these photons.
"According to the Big Bang theory, the cosmic microwave background was =
created when energetic photons ionized the neutral hydrogen atoms that =
originally filled the universe." Is this statement sensible? Why or why not
Submitted by claudias"AT"rice.edu 11/04
This sounds like a homework exercise in some class! I think I've waited long enough to answer it though, that it's unlikely to help get anyone a better grade!
My answer would be that the statement is quite confused. The CMB photons were created in the very early Universe, and in fact you can think of their origin as being from the annihilation of particle/anti-particle pairs at very high energy as the Universe cooled. I don't know what the "energetic photons" in the statement are, if they aren't the CMB photons themselves. And in the Big Bang picture, nothing ionized the neutral hydrogen atoms to be begin with, since the Universe started off hot and ionized. So neutral hydrogen atoms did not fill the Universe at early times.
Please help.
I am doing a project on the big bang thoery and i would like to get
some information out of you.
Please tell me some cool information about cosmic microwave
background; i'll take anything. Information that you did not put on
your site.
Submitted by inherprime"AT"gmail.com 11/04
How do I respond to such a request? Isn't the information on this page more than enough?
The CMB is one of the genuinely coolest things in the entire Universe, being only about 2.735 degrees above absolute zero!
I am an amateur,so sorry for these silly questions: how can we be so sure
that CMB cames from 13 billions years ? And how do we know that CMB has not
changed since then for some unknown reason?
Submitted by FeliciL"AT"ANCE.IT 10/04
Don't apologise for being an amateur - I'm an amateur at many things myself!
We can be pretty sure that the CMB photons come from the early Universe for several reasons. The strongest ones are probably: (1) the "blackbody" spectrum, which can only have come from something in extremely good thermal equilibrium, and the only candidate is a hot early phase in the Universe; (2) the near isotropy of the radiation, pointing to an extremely distant origin; (3) the pattern of anisotropies, which can only be understood as arising from density variations at the time the Universe cooled enough to go from being a plasma to being neutral.
The CMB certainly has changed since it was formed in the early Universe - it's much colder today than it was then!
I have commenced a research paper on dark matter. The cosmic microwave
background seems to be intertwined into dark matter's existence. Can
you brief me on this? Also, can the inferred invisible particles in the
universe exert the enormous gravitational force necessary to keep
stellar galaxies together and in rotation? Or do you think another
force is necessary, and gravity is perhaps a "subordinate" in this
picture (or perhaps even negligible since it is a weak force)?
Submitted by tyro7djm"AT"vfemail.net 10/04
I have to remind readers of this page that I always delay when answering questions which seem to be asking me to do homework for someone!
There are many connections between the CMB and dark matter. Certainly one cannot understand the pattern of anisotropies properly without invoking dark matter. So a recent piece of evidence in favour of cold dark (i.e. "non-baryonic") matter is that there's a direct constraint on the amounts of baryonic and non-baryonic matter coming from the CMB anisotropies. You need about 5 or 6 times as much "cold dark matter" as regular matter.
Although there are several ideas for non-gravitational forces which might be operating on large scales, there is currently no theory which can explain a large suite of different sorts of cosmological information without having this dark matter.
Where does it come from? What are the sources? What are the Proportions in
our atmosphere of alpha, beta and gamma radiation. A pie chart would be
ideal.
Submitted by putnamrm"AT"shrewsbury.org.uk 11/04
This looks like another Cosmic Ray question to me!
The CMB is composed entirely of photons, i.e. very, very low energy gamma-rays, with no alpha or beta radiation at all. So the pie chart would be a complete pie labelled "photons".
was there any one study that
stands out in particular as the "discovery" of the microwave background? Who
has doen the most influential work in this field, and where could I find
articles they have published on this topic?Submitted by Zachary.A.Mayer"AT"Dartmouth.EDU 11/04
Although the early history of the CMB has several twists and turns, it was definitively discovered by Penzias and Wilson, whose discovery paper was published in 1965. You can find out a lot more about them by doing an internet search on "penzias and wilson" for example.
Lots of people have worked on the CMB since those days, both on the experimental and theoretical sides. Robert Dicke did some of the most important early experimental work, with Dave Wilkinson carrying this on for the rest of his career, and eventually having the WMAP satellite named in his honour. There have been lots of other great experimentalists, but since they're mostly still alive, I don't want to get into a prioritisation contest! Modesty also forbids me to name the most important theorists!
I would like to know if
the CMB could be responsible for keeping the electron spinning around the
nucleus of all atoms in living organisms, a little bit as microwave
radiations accelerate electrons in food.
Submitted by slemaire"AT"uottawa.ca 01/05
No. The intensity of the CMB is so low (compared to pretty much anything you can think of that you could generate yourself, microwave or otherwise) that it must have negligible effect on human beings and other living organisms.
Electrons orbit atomic nuclei essentially through the electrostatic force between opposite charges, although you need to throw in some quantum mechanics to understand what's going on in any detail.
If background radiation comes from all directions, why would you need a
horn and waveguide to detect the signal ? Wouldn't a super high gain
transistor detector circuit receive a more accurate signal if it were
direct coupled to a tuned full wave antennae ?
Submitted by king_james_1"AT"verizon.net 01/05
You obviously know a lot more about radio technology than I do!
However, I think you may have things a little confused here. The CMB is very "broadband", since it has a blackbody spectrum, and can be detected over about 4 decades in frequency. So you don't want to tune to any particular frequency (and in fact will lose detection efficiency in a very narrow band detector). The second thing is that the CMB comes from all directions, and so you can point your antenna anywhere, except that you'd like to collect a lot of radiation, and so your antenna has a dish or horn of some sort. But you're certainly right that a high gain transistor might make a good detector.
In your answer to the "How come we can tell what motion we have with respect
to the CMB?" question, there is one more point that could be mentioned. In an
expanding universe, two distant objects that are each at rest with respect to
the CMB will typically be in motion relative to each other, right?
Submitted by danieldarre"AT"yahoo.com.ar 01/05
Correct! The 2 observers will be in the "Hubble flow", i.e. they will be receding from each other along with the expanding Universe. If they're at rest with respect to the CMB, then they won't have any "peculiar velocity" relative to this "Hubble flow".
How would it be seen an object (mass) staying at rest respect to that absolute
(expanding) rest frame, from a reference system that is traveling with respect
to it at the speed of the earth, from the point of view of time dilation due
to relativistic effects.?
Submitted by danieldarre"AT"yahoo.com.ar 01/05
A distant object which is in the "Hubble flow" will be seen to have a redshift as a result of the expansion. You can think of this as simply due to the expansion of the wavelengths of the photons as they travel to you from the distant object, or you can think of it as like the Doppler effect of a velocity (although this really only works for fairly modest speeds, otherwise you have to be a lot more careful).
An object observed at some high redshift will also be observed to have a "time dilation", i.e. the timescales in the frame of an observer there will appear to be longer than your time by a factor of (1+z), where z is the usual sumbol for redshift. The light curves of distant supernovae show just such an effect.
An object which has its own "peculiar velocity" relative to the expansion will be seen to have redshifted wavelengths in its spectrum and a time dilation on its clocks which is an appropriate combination of the 2 effects. Explicitly you have (1+ztotal) = (1+zHubble)×(1+zpeculiar).
I am curious why nobody is curious about the spread of the photons
frequensys when thay where created in the big bang. Why this background
radiation, 1mm to one tenth of a meter?
[abridged]
When energy make photons in the big bang it has all of the spectrum to
chose in why this narrow band?
Submitted by sim"AT"telia.com 01/05
The early Universe is in very good "thermal equilibrium", which means that there are photons with a wide range of energies, with the spread dependent on the temperature that the Universe has. This spread in frequencies is referred to as a "blackbody spectrum", which is a particular mathematical expression determining the precise number of photons at each frequency. This blackbody radiation was once very hot, but cooled as the Universe expanded. All of the frequencies of the photons get redshifted, so that the blackbody shape stays the same, except that it changes to be a blackbody of lower and lower temperature.
So the CMB photons are not from a narrow range of frequencies at all. You may have got that impression from reading about specific measurements of the CMB, which use an instrument which only covers a narrow range of frequencies. But the CMB itself is quite a broad frequency function. Given that the temperature today is about 3 Kelvin, the peak frequency is somewhere around 100GHz. The number of photons has fallen off so much at frequencies corresponding to very long wavelength radio or very short wavelength visible photons that you couldn't hope to detect the CMB in those wavebands. However, you can detect the CMB over a pretty wide range, from a little below 1GHz to almost 1000GHz.
I am also at a loss at understanding the concept of photons cooling after
they have been generated. Is there any URL you can refer me to
explaining/describing how emitted radiation might cool in an expanding
universe (ie. to the current level of around 2.7K). I'm comfortable with
the kinetic cooling of gasses as they expand, but the cooling or reducing
frequency of propagating electromagnetic radiation is has challenged my
knowledge of physics somewhat.
Submitted by jcoldrey"AT"bigpond.net.au 01/05
OK, here's an attempt to answer this question from the point of view of someone who has some basic grounding in physics (say at the introductory college level).
You can think of the CMB as being a "radiation gas", i.e. a collection of photons behaves like a gas of atoms, with the big difference being the relative amount of pressure per unit density. Another way of saying this is that radiation behaves like a gas with a "gamma" (ratio of specific heats factor) which is 4/3, rather than the 5/3 that you have for an "ideal gas" of regular atoms.
This radiation gas will cool if you expand it, just like any other gas, except that the amount of cooling is different because of the different "gamma" factor. So if you want to think of the CMB in this way, then you can understand why it cools, just like a regular gas would. And the amount of cooling explained in this way turns out to be just the same as saying that the energy of the photons goes down as the wavelength of the photons gets stretched along with the expansion.
You have said:
"BTW, a fun fact: the coordinate system defined by the CMB is not inertial!"
May I know why?
Submitted by bhalerao"AT"nuclth.theory.tifr.res.in 01/05
I don't recall ever saying that!
But it's true that you can't fully consistently deal with frames in an expanding Universe within the context of special relativity, but need the full General Relativity theory. Although space appears to be close to flat, it's still not "Euclidean", because it's expanding. So one needs to be careful to set up a framework in which you can talk about a "peculiar velocity" relative to a set of hypothetical observers who are moving along with the expansion.
If the CMB was emitted some billions of years ago and travels at the
speed of light and we have "traveled" from that same point in space time
at lots less than the speed light, how is it that we can see it?
Wouldn't it be long "past" us? And how come we can see it in all
directions? [FOLLOW UP]: I found the answer in your email answers section.
I think I understand it but ... It is not an easy concept.
Submitted by tjax"AT"comcast.net 02/05
I like it when people answer their own questions before I get to it!
You're correct that this is not an easy concept. It may be that different people have different ways of picturing this. But my feeling is that for most people the main difficulty is that they are starting off with the wrong image, and then it's extremely hard to get it right after that. So it might help to totally erase the idea that the Universe used to be smaller (or that it started with a singularity or very small region embedded in some larger space) - instead start with the idea that it has always been infinite in size (even if everything used to be closer together in the past) and take it from there.
Is it logical to maintain (as we appear to do) that the space-time
expansion can affect minute entities like photons by stretching their
wavelengths and yet the same space-time, the curvature of which is
gravity, also holds together galaxies and galactic clusters stretching
only voids between them? Whence this discrimination?
Submitted by adarnay"AT"sbcglobal.net 03/05
This is a very good question! The answer is "yes, it is logical to maintain this", and the best way to think about the distinction is to consider what the space is doing.
As you point out, galaxies aren't expnading along with the distances between galaxies, because they are self-gravitating objects which no longer care about what the rest of the Universe is doing. Photons within galaxies don't have their wavelengths stretched either, since the space within the galaxies isn't expanding (although there could of course be effects arising from velocity or gravitational differences between emitter and observer).
The wavelengths of the photons get stretched because the space is expanding as the photons travel through that space. So it's really only because the photons are propagating through the expanding space that their wavelengths are stretched - or at least that's one way to think about it which I think is helpful to resolve your dilemma.
[abridged]
Specifically, as a photon travels through inflating space and its
wavelength gets stretched, where does the lost energy and momentum go?
Submitted by WHeller"AT"fdic.gov 03/05
The energy goes into the expansion of the Universe!
Could you be a bit more specific? What is the coupling mechanism by
which the universe (or some of its mass or energy) picks up the lost
energy of the cooled photons?
Submitted by WHeller"AT"fdic.gov 04/05
There's no "coupling mechanism". It's simply thermodynamics. Per unit volume of the Universe, the energy lost due to the expansion is equal to the "work done". This has to be true, since all cosmological models are calculated within the context of General Relativity, a theory which manifestly conserves energy.
My major is French Litterature so I am not so familiar with science. But I
guess I understood the relation between CMB, Big Bang and current
universe's temperature being 3K.
However, I don't exactly get the cosmologic? concept or the mental picture
I should be having while thinking about the whole universe. If CMB and our
universe is like our microwave oven, how could we ever measure the CMB from
the past universe - temperature of which should be way higher?
Submitted by doyon1004"AT"hotmail.com 03/05
Thanks for your question. I'm trying to guess what picture you might have in your head in order to try to figure out what sort of answer would be most helpful to you. So I apologise in advance if I get this totally wrong!
You should really s start by removing any idea that the Universe is like a microwave oven! I see nothing very useful in that analogy. But nevertheless we could continue with it, provided you're prepared to think of it as an immense and expanding oven, whose walls are extremely far away! You have to imagine that at some early time the oven was turned on and filled with photons everywhere (actually photons of such high energy that they were gamma-rays rather than microwaves). Then the oven is made to expand (but was always huge in size remember!), so that the distances between the photons get stretched, and the wavelengths of the photons also get stretched along with the space.
Today we live at the time when the wavelengths have stretched so much (compared with the time the oven was turned on) that they have become microwave photons. So we observe microwave photons reaching us from the very distant Universe, and emitted at a time when the Universe was very hot. We can see these photons coming to us from all directions, defining a sphere around us which has radius equal to the light travel distance in the time since the oven was turned on. And provided the walls of this oven are considerably further away than this distance of the "observable part of the oven", then to all intents and purposes we can consider the oven to be infinite in size.
And provided you can picture such a microwave oven, then you can do away with the oven entirely, and you're left with a pretty accurate picture of the Universe!
[abridged]
Im stuck on the problem of light aberration, associated both with
the measurements of positions of the distant star (object) you give as an
example, and the measurement of earths speed with respect to the CMB. It all
comes in the end to the resolution of a right triangle, one of its normal sides been v and one of the others being c. But Ive found few explanations for free
on the web, seemingly at odds between each other.
I was trying to elaborate a consistent word document with a concrete question.
But I think it better, as Cosmology is your field, if you are kind to put me in
c ontact with some information where I can figure out the problem by myself
first.
Submitted by danieldarre"AT"yahoo.com.ar 03/05
I find that "Eric Weisstein's World of Physics" is a good place to start for basic physics principles. You can find a description of stellar aberration here
I noticed that in your response to an earlier question (11/98) to the
wavelength and frequency of CBR your state that CBR is approx 150GHz @ 3K.
How does this relate to Smoot's statement in his book that CBM had an approx
wavelength of 7.35cm IE approx 4080 MHz? Is not this the frequency detected
by Penzias and Wilson?
Submitted by ed.hudson"AT"equilinx.com.au 04/05
The CMB radiation is "blackbody", meaning it has a broad spectrum of wavelengths with a precise mathematical shape consistent with a single temperature (2.725 Kelvin in this case).
The peak of the CMB spectrum (in appropriate units) is at about 150 GHz. However, you can detect it over a wide range of frequencies (or wavelengths). Penzias & Wilson first detected it at quite low frequency, namely 4080 MHz, which corresponds to 7.35 cm wavelength. But that is in fact nowhere near where the spectrum peaks. Anisotropy experiments typically work at frequencies much closer to the peak, since the "foregounds" are much less of a problem there.
In your list of FAQs about CMB, you state that the ratio of photons to
ordinary matter in the primordial universe was fixed when the energy of
those photons fell below that required for pair production. Presumably
this would also have determined the initial temperature of the photon
"gas" in thermal equilibrium during subsequent cosmic expansion. I
would assume that the lightest (stable?) particles that could be created
were electron/ positron pairs, giving an initial temperature for the CMB
of about 1.04 MeV or 1.2 x 10[10] K. But, if recent findings of neutrino
oscillations are correct, these particles also have a (very small) rest
mass. If neutrino/ antineutrino pair production were the threshold
process, it would correspond to a much lower initial CMB temperature.
Am I way off base or is there a grain of substance in my reasoning?
Submitted by skylar"AT"nednet.net 05/05
There is some grain of truth in what you are saying, but also some confusion I think.
There's no "initial" temperature in the expanding Universe. The CMB temperature continues to climb as you push back to earlier and earlier times (until eventually you reach energies where you don't know how to do physics any more!).
Neutrinos interact through the weak nuclear force, and this stops ("freezes out") just about the same time as the electron-positron pairs annihilate - actually a little before. So the neutrinos were already evolving separately from the photons by the time of the last particle annihilations. There should be a background of cosmic neutrinos, with roughly the same density today as the photons. However, because they decoupled from the photons before electron-positron annihilation, then it is predicted that the neutrino background today should have a slightly lower temperature (since the CMB got boosted by the annihilation photons, while the neutrinos carried on having the "old" temperature).
The predicted neutrino temperature is about 1.9 Kelvin. So if anyone can figure out how to measure the background of incredibly low energy neutrinos then we could test this! But remember that high energy neutrinos from the Sun are pretty darn hard to detect, and they have about a billion times the energy.
Redshift has three causes: the rapid recession of an object emitting light,
an extremely massive and dense object emitting light and the streching of
spacetime due to the expansion of the Universe. How does General Relativity
show that the CMB is about 46 Gly (giga light years) away and recedeing at
about 50c?
Submitted by emission_nebula"AT"excite.com 05/05
I'm not aware that all of these statements are true.
General Relativity tells us, in a sense, that all the causes of redshift that you mention are really the same - it's just a question of point of view. For nearby objects it's easiest to think of the expansion of the Universe in terms of the speed of recession of galaxies relative to each other. But for more distant things (where the speed would approach the speed of light) it's much more helpful to think of the redshift as coming from the stretching of distances between objects.
The best estimates for the age of the Universe are between 13 and 14 billion years. We also know that the Universe is expanding, and that the expansion rate has not been constant - in fact it was decelerating for a while, but is now accelerating. So the Universe is "bigger" now than it was when the photons (that we're observing today) left on their journey. For the current best model, taking into account the decelerating and accelerating phases, we get a distance out to the "CMB photosphere" of around 14 Gpc (Giga-parsecs, in astronomer units), which is indeed close to 46 GLY (billion Light Years).
For the speed of recession, you need to be careful to define precisely what you mean. I'm not sure what the "50c" is supposed to refer to. If the CMB was receeding from us at many times the speed of light, then certainly the photons wouldn't be reaching us at all!
i read "Misconceptions About the Big Bang", Scientific American, March 2005.
the authors state that more distant galaxies do excede the lightspeed, c. the
authors also state that we can see galaxies that are receding faster than c.
http://www.astro.ucla.edu/~wright/cosmolog.htm defines cosmic redshift as z =
e^(v/c) - 1 so the speed of any galaxy whose a redshift is 1.7 equals c, and
the speed of any galaxy whose redshift is greater than 1.7 excedes c.
Submitted by emission_nebula"AT"excite.com 11/05
The problem with speed is that it's the change of distance per unit time, and in relativity we know that both distance and time are observer-dependent quantitities. So you have to be very careful about precisely what distance and time coordinate you are talking about before you discuss the speed. There are several ambiguities, for example whose time coordinate do I use? when do I measure the distance? do I divide out by the expansion of the Universe? am I only thinking about things along the "past light cone"?
I read that article by David and Lineweaver, and I'm a great fan of Ned Wright's web-pages. I know all of these people, have respect for their abilities to explain things clearly, and wouldn't argue with them for an instant!
Nevertheless, I think it's conceptually much easier to just think of expansion in the Universe as a stretching of the space in which everything lives, and to expunge all thoughts of speed from the picture! It is certainly true that in some coordinates there are objects which are currently moving away from us faster than the speed of light. But that's not important! Nothing is actually whizzing past anything else at v>c. The apparent speed of distant objects comes from the overall stretching of distances, a concept which is neither in our every day Euclidean or Galilean view of space-time, nor even in special relativity. So trying to think about this "inside the box" of Galilean or special relativity isn't very useful.
I have a question? what caused cosmic microwave background? Please help!
Submitted by bupshaw"AT"uabmc.edu 06/05
It's the left-over radiation from the hot early Universe. There's a lot more information about it on this page!
[abridged] Matter is easily observed to cool to 2.7K,
and radiate at this temperature in a state of thermodynamic
equilibrium with the 2.7K CMB - proof that matter is a
source of the 2.7K CMB, and of long-sought "cold, dark
matter".
Submitted by johnson"AT"cogeco.ca 07/05
Certainly there's a connection between matter and radiation. The "hot big bang" view is that the CMB was indeed emitted by matter, but this was at very early times, when the temperature was very high (and the timescale for approaching a blackbody spectrum was very short). The CMB is observed today at 2.725 Kelvin because the Universe has been expanding.
Local sources of microwave photons just can't make such a precise blackbody spectrum. Besides that, we know about the temperature state of lots of regions of the local Universe, and typically the luminous matter is much much hotter than the CMB temperature. Although we don't know very much about the "cold dark matter", we do know 2 basic facts about it: (1) how much there is, about 25-30% of the total density of the Universe; and (2) that it has very weak interactions, with essentially no coupling to the electromagnetic force. This second fact means that the CDM does not interact with photons of any wavelength, and hence has no direct relationship to the CMB.
i am a final year electronics and communications
engineering student and will be working on my final
year project soon. I sport interest in the field of
cosmic background radiation and was wondering if there
was any possibility of doing a project related to the
field.i have been searching for material on and off
the internet,but they seem too large scale for a final
year project. Could you please inform me of the
feasibility of a project in this field.
Submitted by thahirshahnaz"AT"yahoo.co.in 09/05
It is certainly possible to carry out a project looking at effects in real CMB data. Data in a fairly raw form are available from the Wilkinson Microwave Anisotropy Probe (WMAP) experiment, as well as several others. Precisely what you do with these data is entirely up to your imagination!
If you want to get involved in something more hardware related, then it ought to be possible to build a CMB detector using off-the-shelf components. The CMB is actually fairly bright at cm wavelengths (unlike the anisotropies, which are about a factor of 100,000 times fainter!). You'd need some directionality (so you can tell the CMB from the foreground signal which peaks in the Galactic Plane), and you have to have some method of measuring an "absolute" temperature.
Good luck!
At
http://www.livejournal.com/users/vsevcosmos/11322498.html?thread=1410#t1410
a person claiming to be high school teacher George Peterson claims that "the
microwave contributions from the moving wall of the Local Bubble,
interacting with the interstellar medium, would produce a low temperature
microwave hiss. This radiation, near blackbody, smooth to approximately one
part in a hundred thousand, would have as its' temperature, a value of the
order of ~ 2.79 Kelvins" and that "The entire CMB can be derived from this
sole local effect."
Submitted by vorleons"AT"hotmail.com 09/05
There are several things wrong with this.
First of all, one has to ask oneself, "why would someone be so desperate to find an alternative explanation, when the Big Bang picture naturally makes the CMB"?
When the CMB was first discovered the simplest explanation was that it was redshifted radiation from the hot early Universe. However, the constraints on the isotropy of the CMB and on its spectral shape were not very tight until well into the 1970s. So for about a decade it was perfectly reasonable to consider local alternatives for making this microwave background.
But now, 30 years later, we know that the CMB is isotropic to about 1 part in 100,000 (other than the dipole) and that it has about the best blackbody spectrum which has ever been measured.
Any idea which anyone has come up with to make the CMB locally has trouble with both of these properties. If you make the CMB from some radiating substance, then it will typically have either absorption or emission features, since complete thermal equilibrium is extremely hard to establish in today's Universe. And to make it isotropic you have to imagine some picture where, for example, there's a perfect sphere of material around us (with no variations at more than about the 1 part in 100,000 level) and that we're exactly in the centre and that whatever it's made of has no significant effect on our ability to see distant objects through it. Passing all of these stringent criteria is a very tall order!
But it's even worse than that, since we've now measured the anisotropies with very high precision, and they're exactly what we expect from the early low amplitude density variations of the sort we need to have grown all of the structure in the Universe.
So if you want to make the CMB through some local source, you also have to contrive for that source to give precisely the power spectrum of anisotropies which matches what the standard cosmological picture gives you!
As you already told, the theory of special relativity is based
on the argument that there is no preferred rest system.
Do you think that Einstein would have developed his
theory if CMB were already discovered before 1905?
For example: G. Smoot regarded the CMB explicitly as a
'new ether'. Would Einstein have denied the 'ether' if he
had know about CMB?
Submitted by helmuthansen"AT"t-online.de 09/05
This is an intriguing question. But I'm not sure I'd like to second-guess Einstein! (especially in this centenary year of Special Relativity etc.)
Since the existence of the CMB "rest frame" does not violate the Principle of Relativity (which was a central idea that Einstein came up with to tackle relativity), one would presume that the existence of the CMB would not have thrown him off track.
Incidentally, did George Smoot really say that the CMB is the new ether?!
I just heard on
the radio that CBR is moving in a direction which is different to what
you mentioned on your site. Which direction is it and why do you think
this is?
Submitted by jimidybobidybo"AT"hotmail.com 09/05
First of all, the CMB isn't moving in any particular direction, since all the photons that make it up are travelling at the speed of light from where they last scattered in the early Universe to wherever they're going, in every direction!
But we are moving through the sea of CMB photons, which we can detect through the dipole (i.e. half of the sky is brighter/hotter than the other).
There is no significance to the particular direction. Specifying the direction of our velocity vector obviously depends on what coordinate system you use - so you may see apparently different quantities which are really just the same thing in a different coordinate system. The actual direction of the vector also depends on what parts of out motion you take out. If you were to instantaneously measure the CMB dipole with an experiment on the Earth you'd have to consider at least the following list of contributors to the total velocity: any motion of your detector relative to the Earth; your rotation about the Earth's axis; the Earth's motion around the Sun; the Sun's motion relative to its neighbours (the "Local Standard of Rest"); the motion of this collection of stars around the centre of our Galaxy; the motion of our Galaxy relative to the centre of mass of the Local Group of galaxies; and the motion of the Local Group relative to larger scale structures.
So depending precisely which velocity is being talked about, it's easy to get apparently different quantities which are really the same thing in different reference frames.
If the universe was opaque until recombination because all the hydrogen
and helium was ionized, and if the universe underwent reionization after
the stars formed, why is the universe not opaque again?
Submitted by fbaer"AT"c2i2.com 10/05
This is an excellent question!
The reason is that the amount of scattering just isn't enough.
The distance out to the epoch of reionization is obviously pretty far, but the Universe is also pretty darn empty. The dominant scattering is between the photons and free electrons (other processes have been considered, and are all negligible in comparison). If you calculate how much scattering you get out to (say) redshift 6, the answer is around 1 per cent. Out to a redshift of around 15 it has grown to about 10 per cent. And that's about as early as we think the Universe may have reionized. So we expect that as photons travelled through the intergalactic medium on their way to us, they found it to be about 10 per cent "optically thick". [The early Universe is so optically thick because the density was so high back then]
You may think that 10 per cent is no big deal, but in fact this effect is observable! In fact the extra scattering at low redshift partly suppresses the primordial anisotropies (because the scattering is isotropic), and it generates a large-angle polarization signal, which was detected by the WMAP satellite.
By measuring this very weak signal in more detail we'll be able to learn more about the epoch of reionization, which is really quite exciting!
After sending my questions, I thought about scattering some more. One
thing that occurred to me, and which I believe is implicit in your
answer, is that with expansion of the Universe, the distance between
galaxies and such increases linearly with the expansion but the density
of scattering electrons drops with the cube of the expansion. As
expansion increases, photons travel further between objects but the
number of electrons encountered decreases. In addition, some of those
electrons that caused scattering prior to recombination are now in stars
and other bodies.
Submitted by fbaer"AT"c2i2.com 10/05
Exactly, you got it!
I have a question about the cosmic microwave background which I was hoping
you could clear up. If we are moving towards the high-frequency-wavelength
regions of the CMB (and are currently passing through the
low-frequency-wavelength infrared region, on the electromagnetic spectrum)
will we eventually pass through a part of the CMB with the same frequency
as visible light? If so, what will the universe look like? Someone told me
once that everything would appear white.
Submitted by jharte"AT"wellesley.edu 10/05
I'm afraid your question is based on a misunderstanding (or alternatively, I don't understand your question, which is always possible!).
The CMB currently has a temperature of 2.725 Kelvin, with a peak wavelength in the microwave part of the electromagnetic spectrum. It has this same temperature everywhere in the Universe at the present time. It is getting colder as the Universe expands, and so the temperature everywhere is decreasing all the time. This decrease is pretty slow though, so you'll never be able to detect any difference in your lifetime.
You may be confusing things with the CMB "dipole", which is the fact that one side of the CMB sky is slightly hotter than the other (by about a few milliKelvin, i.e. about 0.003 Kelvin). That's caused by a Doppler shift because of our motion through space. Different observers elsewhere in the Universe will see different dipole directions and amplitudes, depending on their velocities. But you'd have to move at nearly the speed of light in order to detect close to visible light (in the direction to which you were moving) for the CMB.
I was able to see Stephen Hawking tonight at the San Jose CPA.
Mighty cool.
One thing I noticed, was when he showed a picture of the CMB,
pointing out that it is not uniform, it kind of looked like a picture
of the Earth.
Has anyone investigated the various density patterns and
similarities to continents? Could there be some parallels to
continental drift and how the CMB drifted (expanded) into clusters?
Just a strange thought that popped into my head as I was watching.
Submitted by 11/05
I think any similarity to the Earth is because: (a) the whole sky is a sphere; and (b) certain choices for the colour table (e.g. green/blue) will look reminiscent of our "little blue marble".
In fact there are some important differences. The main one being that the features on the Earth's surface contain lots of sharp edges. In terms of fluctuations, this means that there has to be strong correlations between the phases (in other words if you make an image with lots of waves, you need the waves to have their steepest parts lining up to create sharp edges). The CMB sky, on the other hand, has very diffuse structures, with no sharp edges. And as far as we can tell the phases are pretty close to being as random as they can be. This is actually one of the clues that the CMB anisotropies may have been generated during an early period of cosmic inflation, with little subsequent development of their structure. This randomness of the phases is the main reason why your eye can't pick out much of interest in CMB maps - the useful information is contained in the variation of the temperatures as you change angular scale.
my name is Ann and I'm doing a project in school about cosmic radiation.
therefor i would like to know what the background radiation is on the
moon.
Submitted by ann.shenyang"AT"gmail.com 12/05
That's an odd question!
The Cosmic Microwave Background would be exactly the same on the Moon, except for the effects of the Earth's atmosphere.
But I suspect you're really thinking about cosmic rays (very high energy particles which are a potential hazard for astronauts), rather than the Cosmic Microwave Background (very low energy photons which exist in such abundance that millions of them are passing through your body at every instant of your life!).
What is the microwave wavelength corresponding to 2.73 Kelvin of
the CMB?
Submitted by richard.sackhouse"AT"videotron.ca 12/05
The CMB has a "blackbody" spectrum, i.e. a broad range of wavelengths, rather than a single specific wavelength. The peak of the CMB spectrum occurs at a wavelength of about 1 millimetre (depending precisely what quantity you are defining for the peak, e.g. intensity per unit wavelength peaks at a different wavelength than intensity per unit frequency). But the CMB is fairly easily detectable at wavelengths covering a factor of 10 higher and lower than that.
At this page you wrote the common thing: "in fact the ions
and electrons are combining for the first time, so it should perhaps be
called "combination"". I've added such a comment here: "Not at all!
Epoch of "recombination" took a good deal of time, maybe 50,000 years
or so, during which ions and some electrons of already low energy were
combining still many times but as the time passed it happened more and
more rare. Each atom had its own time to recombine at the last time,
after it was last time ionised by the most energetic photon." Is there
any mistake?
Submitted by mvg"AT"credit.biysk.ru 12/05
I think this may be mainly semantics rather than science!
When astronomers talk about recombination they usually mean that electrons combining with the ions to make neutral atoms once more. It's in that sense that the cosmological case isn't really recombination. But it's certainly true that an individual atom is zapping in and out of being ionized as the cosmic recombination progresses.
You can read more details about the process of recombination than anyone would reasonably expected to want to know in our paper "How exactly did the Universe become neutral?", which you can find in pdf form here.
By the way: "the surface of last scattering" should be
a 4-dimensional space-time surface, shouldn't it? I see it was the whole
Universe some period of time. Lo! That's not a surface one can easily
imagine! But from the other point of view, as you write in E-mail
part, the surface or a shell is that we see now... That's our point of
view however and I think, that the first one is more correct, isn't it?
Submitted by mvg"AT"credit.biysk.ru 12/05
I think of the last-scattering surface as a 3-dimensional shell around us.
You're right that one should perhaps be a little more careful than that. However, it's typical in cosmology to assume that all observations take place along the "past light cone", i.e. we can only see things as they were the light travel time ago. So more explicitly the last-scattering surface is a slice through our past light cone, which is a sphere in 3 dimensions.
I have read the following statement in Zaldarriaga's "An Introduction to
CMB anisotropies",( which is much more than a simple
introduction!Unfortunately, it contains several errors, which made me
skeptical about each ab every formula) :
"The CMB blackbody formed at z~10^7 at t = 70(T/2.7)^(-2) hours old".
Now, as far as I know, T/2.7 = 1+z .Putting this value into the formula
gives t = 2.5*10^(-9) seconds, much earlier than nucleosynthesis, which
is supposed to have occurred at z = 10^10 !
Obviously there is something wrong, and I would be grateful if you could
point out what it is.
Submitted by georges_melki"AT"yahoo.com 01/06
The photons which made the CMB were "created" at a redshift of about 107. What is meant by this is that photon-creating processes were very rapid before this, while after this epoch photons were still scattered, but they rarely were created or destroyed.
Matias Zaldarriaga is a smart cosmologist, and rarely wrong! What he's giving is an approximate age for the Universe corresponding to this "CMB creation" epoch. You need a cosmological model to figure out the age exactly, and so I presume he's done this for something like the standard cosmological parameters.
When he writes "(T/2.7)^(-2)", he's just giving the scaling relative to different possible measurements of the CMB temperature. So the "T" in this formula is the temperature today, i.e. 2.725 Kelvin. This means that the "(T/2.7)^(-2)" factor just changes the age by about 2 per cent. The age of the Universe at this epoch was therefore about 70 hours.
In fact at these early epochs the age varies approximately like (1+z)-2. When I put in the coefficients I get about the same answer, i.e. around 70 hours for (1+z)=107. The beginning of the nucleosynthesis period (say (1+z)=1010) was therefore a factor of 106 earlier, or about a quarter of a second.
Is there an equation that I can use to find the temperature of the CMBR
with respect to time?
Submitted by TmanMrT"AT"cox.net 01/06
The CMB temperature is changing along with redshift (usually denoted z) in the expanding Universe according to T(z)=T(today) × (1+z), where "today" corresponds to z=0.
To figure out how redshift relates to time, you need to specify the precise parameters of a cosmological model.
However, if you're only interested in changes close to today, then things
are easier. The result is almost independent of the cosmological model,
except for 2 basic parameters, the CMB temperature and the Hubble expansion
parameter. The equation relating a small change in temperature to a
small change in time is simply: 
T =
-T0 H0 t.
Hence in a human lifetime (let's be generaous and call this a century),
the CMB temperature decreases by about 0.00000002 Kelvin!
Is the CMB a phenomenon that has a wavelength?
Submitted by tan_dapeng"AT"hotmail.com 01/06
The CMB photons have a range of wavelengths, peaking around 1 millimetre in size.
if the cmb was created in the very early timeframe of the universe,my
idea of this is that of an enlarging sphere of photons travelling at the
speed of light.why doesnt this wavefront if you will pass us by.why are
we continually being bombarded with it.it doesnt seem right that it would
bounce around the universe but would travel in a strait line until it
strikes something and then would release its energy
Submitted by timbo2000"AT"austin.rr.com 02/06
"Why haven't the CMB photons already passed us" is in fact the most frequently asked question about the CMB!
There are several extensive answers on this very page.
The quick reply is that your picture of "an enlarging sphere of photons", while very common among people trying to understand cosmology, is entirely incorrect! The "Big Bang" happened everywhere, not at in an isolated part of the Universe. It's much better to turn the picture inside-out and have us at the centre, with photons arriving at us now coming from the very early Universe from all directions. In other words, the earliest moments of the Universe can be seen a light-travel-time-of-the-age-of-the-Universe-ago, in all directions.
Considering that the CMB radiation travels at the
speed of light, and the fabric of space has been
expanding for about 15 billion years, and the CMB you
write about began its journey about 300,000 years
after the Big Bang (say, 15 billion years ago), and
the atoms of our solar system were among the atoms on
a similar journey, it would seem that two
contradictory statements are "true":
1. The CMB represents radiation from matter that was a
distance of 15 billion light years away from our
present solar system location 15 billion years ago.
2. Through a combination of atom movement within the
fabric of space plus the expansion of the same fabric
of space, the atoms of our solar system have also
"traveled" billions of light years, but somehow
traveled so far ahead of the CMB that it took 15
billion years for it to reach us!
Submitted by timjbal"AT"yahoo.com 02/06
I suspect this is another variant of the "why have the CMB photons not passed us" question. But I don't understand exactly what you have in mind, and hence it's not clear to me where your source of confusion lies.
So let me address each of the statements you make, in the hope that this will be helpful.
"the CMB radiation travels at the speed of light" - true! - "the fabric of space has been expanding for about 15 billion years" - also true - "the CMB you write about began its journey about 300,000 years after the Big Bang" right again - "the atoms of our solar system were among the atoms on a similar journey" - this I don't get.
The atoms of the solar system certainly aren't travelling at the speed of light. They've just been expanding away from distant objects, along with everything else in the Universe. You should think of the atoms of our Universe being pretty much where they were to start with. We're seeing CMB photons which were emitted by atoms near to the Big Bang in time, and hence have travelled about 15 billion light years to get to us (actually a bit more than this, because the Universe was expanding during that journey, but this is an extra complication that doesn't change the picture). Likewise there's a place (actually a set of places in a sphere around us) very very far away which is right now seeing the CMB photons which were emitted by the atoms which later made our Solar System.
Sir,how is CMB related to GZK cut-off?
Submitted by amidiptimoy"AT"gmail.com 02/06
The "GZK cut-off" is the idea that the highest energy cosmic rays don't reach the Earth because they interact with CMB photons as they travel through intergalactic space. The acronym stands for Greisen-Zatsepin-Kuzmin, the names of the people who proposed this effect in 1966. Their idea is that the highest energy particles (above about 1020eV) will interact with CMB photons to produce pions. There is currently a controversy about whether the GZK cut-off has been observed in cosmic ray experiments, and if not whether it points to some new physics.
Like dozens of people on your question page, I am confused regarding the
idea that the radiation has somehow not already passed us. But please don't
close the email here!!!! - I will refine the question so that it is more
precise.
I understand that the universe has no centre and I noticed that in many of
your explanations to the problem you said that the universe was not smaller
in the past. But most theories of the Big Bang I have read state that it
all began as a singularity. Even my course text book (Cambridge, for 16-18
year olds) says this.
Even if the universe did not begin quite as small as a singularity, the
speed of expansion of the universe is still much smaller than the speed of
light. So by now there should be no radiation left to ever pass us.
Submitted by ruby_murray1@hotmail.com 02/06
The idea that the Universe started with a singularity is an old one. It was essentially proved by Hawking and Penrose and was a tour-de-force of classical cosmology (circa 1970). Here "classical" means General Relativity, with no quantum mechanics. For the last 25 years or so (at least) our ideas for the earliests stages in the history of the Universe are rooted in quantum fields. We know that (running the clock backwards in time) as the Universe gets denser and denser, and hotter and hotter, we eventually come to an epoch when we really don't know the physics well enough to know what is going on, because we need a theory of quantum gravity.
So most cosmologists, if they have a mental picture of the first stages of cosmic history, do not have a singularity as part of the picture! Probably it's some fuzzy mess, maybe with strings or branes, or multiple dimensions, or eternally inflating universes within universes, or some other thing entirely. And who knows, one of them may even be right! But please erase that sentence from your textbook, since it's certainly not the consensus view of the world's cosmologists right now, and hasn't been for at least a quarter of a century!
The other problem with the singularity idea (often followed by a phrase like "and then it exploded") is that it sucks people into the fallacious idea that the early Universe was localized. Thinking along those lines is the path towards misery and despair!
Think of the earliest Universe along something like the following lines and things will be much clearer. I can't promise enlightenment, but I can promise that you'll at least have the hope of understanding why the CMB photons haven't already passed us!
So for the very first instant, no one really knows, but it's not localized! Then very shortly after that, you think of the Universe as being big, maybe infinite, and it's all expanding. In other words the "Big Bang" was everywhere. And today's photons simply come from however far away photons get in the age of the Universe.
so do these photons make up a finite universe or do they incase a finite
universe? or are they infinite going where there is no matter?
Submitted by Jacquianne701949"AT"aol.com 02/06
The simplest picture we have of the Universe is that it's infinite in space. So there is matter everywhere, being distributed pretty much the same way as it is in our observable patch. And there are photons everywhere too, going at the speed of light in every direction. Today we're seeing the ones which come from the light travel distance in the age of the Universe.
although wavelength of microwave is not of order of microwave then why it
called microwave?
Submitted by geeta_with_love"AT"yahoo.com 03/06
The precise definition of "microwave" is fairly murky. A common definition is that it covers frequencies of 300 MHz to 3 THz. The CMB blackbody spectrum certainly peaks inside that range. It's true that the spectrum extends into the "radio" and "infra-red" regimes. But it's fair to refer to is at the Cosmic Microwave Background, because that's the waveband in which most of the radiation lies.
i have to given an interview and i give my intrest of field microwave.i
think they asked the first question- although wavelength of microwave is
not of order of micro then
why it called microwave?
Submitted by geeta_with_love"AT"yahoo.com 03/06
Ah, so I think this is a different question! Why are microwaves called microwaves at all, given that you might have expected that to apply to wavelengths measured in microns (rather than millimetres) - so why "microwaves" instead of "milliwaves"?
I don't know the answer to this! It's a bit like one of my favourite mysteries of the Universe: "why is a grapefruit called a grapefruit"?!
As far as I can tell (looking up dictionaries) "microwave" was first coined in 1931, but I'm not sure by who, and whether the definition has changed since then. Apparently "microwave oven" dates from 1965, "microwave" as a shortened form in 1974 and the verb "to microwave" in 1976.
Assume: The Big Bang occurred
(1) At some single place in the universe( the size of a dime) many
billions of years ago
(2) There is no evidence to support the theory that there were other
places where Big Bangs occurred simultaneously
(3) Within about one minute after the Big Bang, matter cooled and began
to emit micro waves
(4) All the matter has been expanding and the microwaves have
been radiating ever since, so the present size taken up by this diffused
matter is immensely larger, relative to the size it took up at the
instant of , or within one minute of, the Big Bang.
Questions:
(1) Why is the "signal strength" of the CMB the same from any direction
in the universe?
(2) Would it not be strongest from the direction of that single , and
much relatively smaller, ancient location of the Big Bang? ( wherever
that precise location may be, being irrelevant)
(3) Would it not be weakest ( or non existent) if we aim the telescope
180 degrees away?
Submitted by sidgold"AT"rogers.com 03/06
This is a variant on the single most asked question about the CMB - "why haven't all the photons passed us already?" - which has been answered on this page many times before. I urge you to scan the page for answers to similar questions, so you can find the answer that resonates the best for you.
The basic answer is that your very first assumption is incorrect. The Big Bang did not happen "at some single place in the universe". It happened everywhere!
How do you derive the age of the universe from the present value of the
CBR wavelength(s)?
Submitted by pauladriaenssens@pandora.be 03/06
You don't!
The age of the Universe is one of the parameters that comes out of fitting the CMB anisotropies to a suite of models. It has nothing to do with the wavelength spectrum of the CMB. The CMB is getting cooler all the time in the expanding Universe, but that can't be used to learn anything useful about how long the Universe has been expanding unless you have a good idea for what the temperature of the Universe was at some early time. In fact there's no theoretical prediction (that I take seriously at least) for the CMB temperature, and hence its measured temperature isn't a useful constraint on cosmological models.
But the variations in temperature on the CMB sky (i.e. the anisotropies) are very useful in pinning down the precise values of the parameters that describe the Universe, including its age.
how did Arnpo Penzias and Robert wilson find CMB?
Submitted by taytaytwinkle"AT"yahoo.com 04/06
Penzias and Wilson were working for Bell Labs, investigating microwave transmission in the atmosphere (the kind of research which led to today's cell phone technology). The "background hiss" that they always measured in their detector turned out to be the Cosmic Microwave Background.
could you tell me why the expected "sea" of relic
neutrinos (from big bang) have lower energy than the cosmic microwave
background? Is it somehow connected to that the neutrinos decuopled before the
photons? I'd really appreciate an answer!
Submitted by Evelina.Olofsson.2152@student.uu.se 04/06
I think you've answered the question!
The basic idea is that the neutrinos "decouple" (i.e. stop interacting with other particles in the Universe) just before the annihilation of the thermal electrons and positrons (which existed in approximately equal numbers and were about as common as photons at temperatures corresponding to energies above their rest mass). So when the e+-e- pairs annihilated, that created more photons, boosting the temperature of the photon background relative to the neutrinos.
A fairly precise calculation can be done by simply considering entropy before and after the annihilation, and some understanding of the statistics of bosons (photons) versus fermions (all the other particles). The answer is that today's CMB photons occur everywhere with around 400 per cm3 and with a measured tempertaure of about 2.7 Kelvin, while the neutrinos have a temperature of about 1.9 Kelvin and there are about 100 of them per cm3 (per neutrino species). Doing the calculation
I know that ionizing radiation is simply a radiation that has enough
energy to break chemical bonds. Also, I have researched and few websites
categorized cosmic radiation as a form of ionizing radiation. But does
`Cosmic Microwave Background Radiation' carry enough energy to break
chemical bonds? I mean, it is only in the range of microwave. To my
understanding x-rays and gamma rays are only two types of rays in the
electromagnetic spectrum that carries enough energy to do so.
[abridged]
Submitted by djseo0913"AT"yahoo.com 05/06
I think you're confusing the CMB with Cosmic Rays. CMB photons don't have enough energy to ionize anything today (although they did in the early Universe). Cosmic Rays, on the other hand, can be very high energy indeed.
Please check other answers on this page!
What if CMB were not
considered an "echo" as such and was looked upon as a carrier wave for
all forms of matter and energy, wouldn't that necessarily lead to an
explanation for the comings and goings of the universe (e.g. matter,
radiation, particl physics etc...) and lead us a damn sight closer to
"fundamentals" of the universe and the origins on which they would all
impinge ? A good example being sound, harmonics, resonance and
fundamentals as encountered in basic wave mechanics ?
Submitted by fhudson"AT"midsouth.rr.com 06/06
I'm not sure what you mean by a "carrier wave". One of the amazing things that was learned about electromagnetic radiation more than a century ago is that it doesn't need a medium to move in, but will just travel through empty space at the speed of light. That's what CMB photons are - just energy from the early Universe which has travelled through space for roughly the age of the Universe. In some kind of desperate analogy we could say that space itself is the "carrier wave" for all of the particles and waves which fill the Universe.
I think we have a pretty good "fundamental" description of the state of the Universe today, and its constituents (ordinary matter, dark matter, dark energy, neutrinos, photons, gravity waves, etc.). We still have only taken small steps to understanding the origin of everything, or in other words the very first instants of the history of the Universe. But the hope is that by studying cosmological information in more detail (and the CMB in particular) we'll learn more about the "why" type questions that relate to the origin of everything, and may find some explanations for the Universe being the way it is.
If the anti-particles and matter particles annihilated each other for
the last time and by some asymmetry some more matter particles were
present that resulted in the formation of the modern day galaxies,where
does the anti-particles come into existence now?as they must have been
annihilated in the early universe,otherwise they would not allow matter to
be formed if they were present to this very day..
Unless some barrier results in their isolation from the matter
particles.Could u please solve this analogy?
Submitted by 06/06
There are no anti-particles today! At least there's a negligible amount left over from the early Universe. And the only existing anti-matter particles are formed from high energy collisions in the interstellar medium. When a very high energy particle collides with a heavy nucleus it breaks off lots of little bits, often including some anti-electrons, anti-protons, etc. We can detect some of these in Cosmic Ray experiments, for example. But only a very very small amount of the matter in the Milky Way is in the form of anti-matter, and the same goes for today's Universe as a whole.
What is the significance of the Cosmic Microwave Background?
Submitted by dbrunn1662"AT"rogers.com 07/06
The existence and spectral shape of the CMB provides very strong evidence for the "hot Big Bang" picture for an evolving Universe which used to be very much hotter and denser.
The "anisotropies" observed in the CMB provide constraints on mechanisms in the even earlier Universe which made the variations in density which grew into all the structure we observe around us today, and at the same time they lead to precise measurements of several quantities which describe the contents and evolution of the Universe.
i have a few questions for you if you could answer then for
me that would be great ok.
the wavelenght
where the radiation come from
how to detect the radiation
how the radiation can be useful
other interesting information
Submitted by justin.19"AT"hotmail.com 08/06
I suggest that for a start you read some of what is on this page! There's also general information at places like Wikipedia.
The short answers to your questions are: the CMB has a range of wavelengths; the radiation came from the hot early Universe; it is detected with a radio, microwave or infra-red detector; it is useful because structures in images of the CMB sky can give us precise information about the Universe on the largest scales.
At some time, won't the distance to the surface of last scattering
increase sufficiently so to be outside our observable Universe, and thus
eventually CMB photons will no longer be visible to us?
Submitted by mbohon"AT"comcast.net 10/06
It's easiest to think of the "Observable Universe" as being the volume from which we can detect photons from earlier times, and hence the "Last Scattering Surface" is essentially identical to the edge of the Observable Universe. The size of the Observable Universe is a little bigger than the distance to the Last Scattering Surface, but only a little (in astronomical terms), and moreover it's hard to see beyond this surface (because of the scattering of course!), and so for all intents and purposes you can consider them to be the same.
We can in principle see neutrinos coming from much earlier times, and hence the "neutrino scattering surface" is slightly bigger, and closer to the true size of the Observable Universe. Gravitons could also come from much earlier, etc.
When these issues are discussed in popular cosmology texts, things are often simplified, to say that we can't see the part of the Universe moving away from us faster than the speed of light, and that the edge of the observable Universe is set by the distance at which the recession speed is the light speed. However, this is a simplification! The whole business of speed in cosmological models is something where one has to take great care, since there can be several different definitions of position and of time (you have to ask things like: "the speed of light measured when and using what distance coordinate?"). The truth is that using the most natural definition of what speed means, you can in fact see the light that left some objects which are now moving away from us faster than the speed of light! I realise this may sound a bit confusing, but I wanted to at least lay this out so as not to be telling untruths! To get a deeper understanding I'm afraid there's no substitute for studying cosmology in its full mathematical glory.
But the bottom line is that you should think of the CMB "LSS" as defining the edge of the Observable Universe.
One wrinkle on this is what happens in the future of a Dark Energy dominated model though! Because as the Universe expands faster and faster the fraction of the Universe that you can see actually shrinks.
And with that I'll stop adding elaborations, since you're probably now even more confused than before!
Hi Douglas, would you mind explaining the evolution of the CMB, ie: it
started at a high temperature, therefore, different wavelength, and
continues to cool, presently at microwave frequency, but not for ever?
Submitted by 909453"AT"@bigpond.net.au 10/06
You have it just about right!
The CMB started in the early Universe when everything was very high energy. You can think of it as a "gas" of photons existing everywhere and having a "thermal" distribution of energies (or wavelengths) characterised by a very high temperature. As the Universe expanded the CMB cooled, a bit like a regular gas does when you let squirt it into a big empty cavity. At the moment the CMB has a temperature of about 2.7 Kelvin, meaning that its spectrum peaks at microwave wavelengths. And in the future it will get increasingly colder, presumably for ever!
I have just finished "The Big Bang" by Simon Singh and it made me think
about the CMB.
As I understand it, the CMB was produced when the universe cooled enough for
plasma to condense into gas and the photons suddenly found themselves in a
transparent universe. My question is what about before that? When the
universe was younger/hotter and the nucleons were bashing about freely the
gluons would be constantly interchanged between them. But when the universe
cooled enough for atomic nuclei to form wouldn't there be the equivalent of
a burst of CMB but with Gluons instead? So shouldn't there be a Cosmic
Gluon Background (CGB or "Cosmic Glue". The detection and variations of
which may yield more information about the early universe.
Submitted by rich_mar"AT"sympatico.ca 10/06
This is a good question!
You're sort of right. But you can't have freely-floating gluons, since they have to be bound up with quarks. What does happen though is that during nucleosynthesis there are photons (gamma-rays in this case) emitted during the nuclear reactions which are going on - basically the binding energy of the nuclei is liberated as photons. These photons add to the CMB and raise the temperature a little. But our Universe has about a billion photons for every nucleon, and so the temperaure of the CMB is only raised by about a billionth!
At slightly earlier times there were lots of interactions involving neutrinos (converting protons and electrons into neutrons for example). When those reactions stopped happening as much, the remaining neutrinos (which unlike gluons, don't interact with much of anything) formed the cosmic neutrino background, which is indeed just like the CMB. And at even earlier times, annihilations between electrons and positrons (anti-electrons) - and between higher mass particles and anti-particles - led to burst of gamma-rays, which boosted the CMB temperature. So in fact the "origin" of CMB photons are particle/anti-particle annihilations in the early Universe.
I am confused about which paper actually
first predicted the CMB. I have looked at the Alpher
Bethe Gamow paper, but cannot distinguish where there
is a direct prediction. Also, the Wikipedia site is
not consistent in attribution, citing both the above
paper and the Alpher-Herman paper. Beyond this,
Alpher and Herman later revised their predicted temp.
to 28K, so it seems they might not have really nailed
down the theory.
Given the above, if I mention the CMB as being
evidence for a Big Bang, do you think that it would be
sufficient to cite textbook souces like Misner Thorne
and Wheeler?
Submitted by bicycle_physics"AT"yahoo.com 11/06
The question of when the CMB might have been predicted is a very murky business! Alpher, Herman and Gamow certainly worked out some details of what we now call the "Big Bang" picture. And they published several versions of a prediction for the temperature of the background radiation - although exactly how seriously these calculations were taken is unclear. Nevertheless, Dicke certainly predicted that there would be a background and set out to detect it, being beaten to the post by Penzias & Wilson, who originally didn't know the significance of what they had found.
And that's the short version!
The evidence for the Big Bang picture (i.e. the Universe once being very much hotter and denser) came later, when it was clear that the CMB has a very nearly thermal ("blackbody") spectrum. So precisely who you should cite for that is also unclear!
But if anyone asks, you can tell them I said it in 2006!
I have been doing some research on the possible effects the CMBR
could have on our natural world. I have taken the frequency down by 29
octaves and found it to be a perfect D. I then made a number of
high-definition audio recordings of various natural sounds, such as a
river and a heavy rain shower, bird calls in a forest, the ocean, etc.,
and put them through a spectrum analyzer. I thought that I might find
dips, or interference, in the spectrum at that frequency, or its
harmonics. What I have found is truly amazing! In every case there seems
to be some influence at that frequency. Do you know of any studies that
have been done, or are being done, about this subject? Or do you know
anybody that might be interested?
Submitted by tedargo"AT"comcast.net 11/06
This sounds intriguing as an artistic project. But I'm afraid that the connection with anything scientific is fairly tenuous. The CMB spectrum is a spectrum of photons, not sound waves. And it's a "continuum", which peaks at a particularly frequency but is fairly broad - hence it could never sound anything like a "perfect D", but would rather sound like noise if intrepretted as sound.
For a different view on "the CMB as sound", used as a pedagogical device for understanding the "acoustic signatures" in the CMB power spectrum you should look at the web-page of Professor Mark Whittle of the University of Virginia, which I've linked here.
The temperature of the background radiation has dropped in due time.
Question: where is the energy, which should be freed by the drop down of
the temperature of the radiation ??
Submitted by Eric.Hoyng"AT"hetnet.nl 11/06
This is a commonly asked question, and so there are other relevant answers on this page.
The short answer is that the energy per unit volume is conserved, and goes into the expansion of the Universe. It's the same as an expanding gas in a box - the pressure of the gas does work in expanding the box, and this "work" is the energy lost in cooling the gas.
I do not understand why the
photons that comprise the CMB have not arrived at thermal equilibrium. I
think you answered the question by saying that these photons are a
different kind of "stuff." Coiuld you be more specific? Are they a
different class of particle?
Submitted by fish9999"AT"netvision.net.il 12/06
Photons are massless particles which carry energy and momentum and interact through the electromagnetic force. So they are quite different from matter particles, like atoms or ions or electrons.
The CMB photons have arrived at thermal equilibrium. That's shown through their "blackbody" spectrum, with a temperature of 2.725 Kelvin.
The photons achieved this equilibrium at early times, when the Universe was very much hotter and denser, and interactions between the photons and matter particles were common. After the Universe stopped being a plasma (at redshifts around 1000, or about 400,000 years after the Big Bang) the photons stopped interacting much with the matter, but cooled with the expansion of the Universe, retaining the blackbody spectrum with an ever decreasing temperature. And that's what we observe today.
I have one more question that I
hope you will answer. What is meant by a "massless" particle. Since a photon
carries energy, and mass and energy possess an equivalence, so doesn't a
photon have to possess mass?
Submitted by fish9999"AT"netvision.net.il 12/06
No, a photon doesn't need to have mass in order to have energy. Much of what we learn about concepts such as mass, energy, momentum and speed are learned for "Newtonian mechanics", i.e. the laws of motion which apply to everyday objects moving at relatively slow speeds. One of the basic motivations of "Special Relativity" is to understand how things behave as you go to much faster speeds.
One outcome of this is that you have to slightly change your notions of those physical quantities. Energy is a thing which can exist in many forms, but is always conserved (e.g. rest mass has an equivalent energy, and you can in principle destroy rest mass to create more kinetic energy). Photons possess "pure energy" with no rest mass. They also have momentum, even although they have no rest mass (and Newton would say that momentum is just mass times velocity). In Special Relativity the quantity called momentum is the thing that stays constant if there's no applied force. You know that photons have to have momentum, since they exert a measurable force ("radiation pressure"), e.g. when you bounce them off something.
You can think of photons as having just pure motion energy, with no rest mass. If you converted the photon's energy into rest mass then you'd have a massive particle, which would have no motion energy - or you could make a lighter massive particle with some motion energy (i.e. travelling at some speed, less than the speed of light). A photon is a very special particle in the sense that it really has zero rest mass and is travelling at exactly the speed of light!
If the theorized Big Bang happened in a specific point beginning the
space/time we experience, why anisotropy and this spectrum of microwave
radiation found in all directions instead of from that point or points in
the singularity event?
Submitted by ajwps"AT"yahoo.com 12/06
Let me say a few things in response to this: (1) the Big Bang is indeed a "theory", but this means that it is a well supported idea, rather than merely an untested hypothesis; (2) when cosmologists talk about the "Big Bang" theory, they mean the model in which the Universe was once hotter and denser and has been expanding, they explicitly do not mean a theory for the first instant that started that expansion (despite what you might think from the name); (3) the expansion happened everywhere at once and not at a point in space; (4) the question that you ask is very similar to others answered on this page, along the lines of "why don't the CMB photons come from one direction?" or "why haven't the CMB photons already passed us?"
... I am also required to understand and explain what
Cosmic microwave rdaiation is. I read your article and am still having a
difficult time understanding exactly what it is. i have searched on the
internet and have yet to come across an explation that i can understand
well enough to explain it in my own words. I was wondering if you could
send me a brief but clear defintion of what CMR actaully is. [abridged]
Submitted by stephanierandall"AT"rogers.com 1/07
Since I don't know precisely what your background is, it's hard to figure out how to explain it to you. Besides which, you should do your own homework!
The CMB is radiation left over from the early Universe, which has cooled as the Universe expanded, and today has a spectrum consistent with a single temperature of slightly less than 3 degrees above absolute zero.
I have a question regarding an answer you gave to sombody else
about why the CMB hasn't 'passed us' already.
I too have wondered the same thing as this guy many times, and often
received a similiar answer. It seems to me that an assumption is being
made (but not stated) in this answer, that being: The inflation of the
(early?) universe must have been much faster than the speed of light..?
The logic being that when you mention photons from this point (here)
having travelled away from here at the speed of light for 14 billion
years - they are still 'getting somewhere' i.e. the universe has gotten
larger than 14 billion light years in diameter, yet has acheived that in
around 14 billion years.
Is that correct or am I also interpreting things wrongly? I see in your
other answers that you say the early universe is also infinite but closer
together, yet I'm still a little puzzled about it.
Submitted by Brett.Melling"AT"uea.ac.uk 1/07
You're pretty close to the right picture I think!
But you don't need inflation in order to have the Universe big enough and full of CMB photons. What you need is some sort of acausal process which starts off everything at once. "All" it takes to make a Big Bang is to have an infinite space which is all very hot and expanding, with the "starting gun" being the same everywhere. (Remember the "Big Bang" isn't the very first instant of time - which no one can picture - but the expanding phase just after that!). Then we see the CMB photons from the parts of the early Universe which are the light-travel-distance away from us. That's really all there is to it. The Universe has always been infinite, or at least much much bigger than 14 billion light years in size.
The thing that inflation gives you is a kind of explanation for that apparently acausal behaviour. A small patch, which was in causal contact at some very early time (i.e. smaller than the light travel time in the age of the Universe) expanded exponentially, at effectively faster than the speed of light, so that it appears to be acausal. But everything in that patch "knew" to start the Big Bang at the same time, and hence the CMB temperature is the same in every direction within the observable Universe.
I read about the neutrino oscillations theory. According to
this theory neutrinos are supposed to have small but non-zero masses.
I am enthusiastic to know about what is the effect of this theory on
CMB spectra.
I also read that there is a problem with the mass hierarchy in
neutrino oscillations and due to their small massed it's difficult to
determine it. However, if one studies the early universe then we have
a huge number of neutrinos and their interactions with rest of the
constituents. So, effectively there is a considerable mass of
neutrinos and effects of different hierarchy should be different. Is
it possible to know about the neutrino mass hierarchy by studying the
implications of neutrino oscillations on cosmology?
Submitted by suchita.kulkarni"AT"gmail.com 1/07
Neutrinos have an effect on the CMB anisotropies because they contribute to the mass-energy density budget of the Universe, and so make it expand faster. The number of neutrinos per unit volume is essentially known (because we know how they interacted in the early Universe, and hence how many of them are left). Hence the CMB (plus other cosmological probes) can be used to constrain the total mass of the neutrino species. At the moment this is just an upper limit, but there may one day be a detection of the neutrino masses in this way. Put together with other experiments, which typically measure neutrino mass differences, one can piece together details of the model parameters describing neutrino oscillations.
The additional effects of neutrino oscillations on cosmology are far more subtle, and I'm not aware of any realistic way of directly constraining the physics of neutrino oscillations using cosmological data.
If an aircraft flies out , and an observer looks up with a cmb
telescope , should he be able to observe the aircraft by its
cmb sillouette ? Is cmb radiation able to pass thro metal
or dense carbon material ?
Submitted by alikaren"AT"blueyonder.co.uk 2/07
There's nothing magical about CMB photons, so you're right that they wouldn't pass through some thick piece of opaque material. In principle you could therefore see the silheuette of an aircraft if you had a high resolution microwave telescope. However, in practice the aircraft will be emitting strongly in the infrared, and so because it's much hotter than the CMB, it will be appear very much brighter!
As well as being an emitter of radiation, the atmosphere itself absorbs some of the CMB photons, this being a strong function of wavelength, and of where you observe from (e.g. the water molecules in clouds will absorb very strongly in a whole bunch of spectral bands). Intergalactic space is pretty empty, as is the space between stars and planets. So most CMB photons travel happily through the Universe from when they were made, shortly after the Big Bang - but a tiny fraction of them happen to be arriving at planet Earth right now, mostly absorbed by the atmosphere or the ground, but a few reaching the detectors of CMB experiments, and allowing us to learn about the Universe!
This started when I read something about the "dark ages" after +380kyears
big bang. Shouldn't that be "dull red" ages? So I did some calculations
and came up with a SWAG of 4 Byears ago to get to about 373K and 2 Byears
ago to get to 273K, which means that that the early univerese was hot, and
no liquid water before 373K and no ice before 273K. So pasturized? Final
conclusion - The Drake equation assumes an equeal distribution through
time for ETI's, if 373K was only 4 Byears ago and life started on earth
3.7 Byears ago, we could be #1 in the galactic intellegence game. Is SETI
a waste of money? Are we alone out here? Is the universe too young to
have generated an equeal distribution of ETI's?
Submitted by markgoll"AT"wt.net 3/07
I think you have the right general idea, but unfortunately you're calculations aren't completely correct.
The relationship between temperature and time in the expanding Universe is a slightly complicated one, because of the different components (radiation, matter and dark energy) which dominate the evolution at different times. The simplest thing to do is to take the age at the "last scattering epoch" for CMB photons and work forwards.
The last scattering epoch was at a redshift of about 1000, corrsponding to
an age of about 300,000 years. Your question asks about conditions in the
Universe when T=273 Kelvin, i.e. when the redshift was about 100 compared
with today (so that the wavelengths of all CMB photons were 100 times
smaller and therefore the temperature was 100 times bigger). It turns out
that during this phase the Universe evolved so that age was proprtional to
redshift to the negative 1.5 power (t
z-1.5). This means that 300,000 years at z=1,000 implies
an age of about 10 million years for z=100.
Hence when the temperature of the CMB was at the boling point of water, the Universe was only about (1/1000)th of its present age. So this was long before there were any alien civilizations in existence. In fact, since structure builds up from very small contrasts in density at early times (the variations in density giving us the CMB anisotropies), there was very little of anything in the Universe at that time. Everything was very smoothly distributed, and stars hadn't yet had a chance to build up the heavier elements. So not only was there no alien life, there weren't any planets or water yet either!
Hi, is it possible to see the radiation with the naked eye (not via the
TV set)? oes it have a frequency on the visible spectrum?
Is there a website with more detailed info about it?
Submitted by joely"AT"framedestination.com 3/07
The short answer is "no". The CMB spectrum eaks in the microwave part of the spectrum, which is several thousand times longer than the wavelengths that your eyes can detect. However, since the CMB cools in the expanding Universe, then it used to be much hotter. So if you had lived in the first few hundred thousand years of the history of the Universe, then the CMB would have peaked in the visible part of the spectrum. Then it wouldn't only have been visible, it would have been really bright!
Could you provide me with a good average number for cosmic
background radiation levels at the Earth's surface near the 1.57542GHz
frequency in dBW? I have heard a lot of numbers thrown out, but because
in circuit thermal noise is usually of more concern than CMB the numbers
are usually left vague. Anyway, I was hoping to get a number to set the
record straight. Also, if you know of a database for current CMB levels
I could reference that would be helpful for the work we are trying to
do.
Submitted by Daniel Healey 3/07
I'm not sure you are really asking about the Cosmic Microwave Background here, or about other potential sources of background noise for terrestrial-based instruments operating at microwave frequencies (or centimetre waves in this particular case).
But if it's really the CMB you're after, then the answer is simple, since it's just a blackbody. So the amount of energy per unit time per unit area per unit frequency is just given by the Planck formula (which you can easily look up if you're not familiar with it) with temperature T=2.725 Kelvin. You can plug in the frequency you're interested in, and use whatever units you prefer. If you want a total power unit, then you'll need to multiply by your bandwidth and the area of the thing you're interested in. E.g. at 1.57GHz, with a 1MHz bandwidth then a square 1mm across sees about -200dBW (in these units), which I think is pretty small by any standards!
I'm wonder, two things, actually. First, can
you tell me the flux of the cmb (in watts per metre square)? And
do you have any idea why it has been so impossible for me to find
that value anywhere on-line?
Submitted by misterpink"AT"mail.com 3/07
The reason this value isn't written down explicitly (very often) may be because it isn't usually the most relevant quantity, but is easily calculable anyway.
A more relevant quantity might be the flux density, i.e. the energy per unit time per unit area per unit frequency, or perhaps that quantity multiplied by some bandwidth. That's because the CMB spectrum is quite wide, and most kinds of detectors have a much narrower range of frequencies to which they are sensitive, and hence wouldn't see all of the CMB flux. Another issue for real detectors is that if they have some directionality (i.e. only receive radiation from a limited solid angle) then they'll only see part of the CMB.
If it's really the total flux that you're interested in, then that is just obtained from the 4th power of the CMB temperature times the Stefan-Boltzmann constant. This comes out to be about 3.13 × 10-6 W m-2.
...then I'm wondering, is there any difference in flux, or flux density, of the
cmb at different latitudes (like there is with the Sun). My (very limited)
understanding of the cmb was as a constant source everywhere and in all
directions.
My interests are actually _climatological_. Though the cmb is quite small,
as you say, I'm curious if it produces any surface or atmospheric effects,
if it gets 'knocked around' by greenhouse gases, if there's a 'cmb
constant' (like the Solar constant) contributing energy to Earth systems
- things like that.Submitted by misterpink"AT"mail.com 4/07
The CMB doesn't depend on latitude on the Earth, and as you suggest, it comes equally from all directions.
I very much doubt that there are any significant effects on the Earth's climate, weather or anything related that might affect human beings. This is not only because the magnitude of the CMB is small by terrestrial standards (it's only important because it's absolutely everywhere in the Universe!), but also because the driving effects for weather and related phenomena are differential, i.e. it's changing factors which have big effects, while the CMB is about the most constant thing you can think of!
It is said that the expansion of the universe "cooled" the radiation.
What is the mechanism by which the wavelength of the photons is changed??
Submitted by suegoss"AT"ecentral.com 4/07
There are several different (and equivalent) ways to think of this. Probably the simplest is just to realise that any expanding gas gets colder. "Radiation", i.e. a "gas" of photons, behaves pretty much the same as any other gas in this regard, although actually it cools at a different rate than a regular gas of particles, since the pressure for radiation isn't negligible like it is for "matter". So the explanation is just that this is part of the usual laws of thermodynamics.
Is this microwave background radiation the empty space between objects?
Is this mbr what is behind the universe in expansion? Imean if the
universe is expanding there must be something behind waiting to be
fullfill? If the universe is 74% dark energy,22% dark matter and only 4%
atomos that fill the visible universe? where this mbr come from?
Submitted by jacomiz"AT"hotmail.com 4/07
The contribution of the CMB to the energy density budget of the Universe is quite small, about 0.01%. So in today's Universe it has a nearly negligible effect on how the expansion evolves. The dominant effect today comes from the Dark Energy, although in fact the CMB dominated in the earlier history of the Universe.
I've been trying to find a figure for the Cosmic Background power
density (Wm^-2) as received here on Earth. I could probably arrive at a
figure based on a black-body cavity model, but I don't have the
necessary figures. I've seen graphs for power per unit wavelength, and
integrating the graph should again produce a figure.
However, I suspect that someone, somewhere, has it written down.
Submitted by sidhedark"AT"yahoo.co.uk 4/07
You can work it out directly from the CMB temperature, under the assumption that it's a "blackbody". In that case the total flux is just the 4th power of the temperature multiplied by the Stefan-Boltzmann constant (about 5.67 × 10-8 in SI units). This gives approximately 3.14 × 10-6 W/m2.
So, the radiation was emitted by gas that was around half the temperature
of the sun. Why does it now take the form of a 2.73 K blackbody?
Submitted by bigpapaskills"AT"gmail.com 4/07
The Universe is expanding and so the radiation cools, while retaining its blackbody form. One way to think of this is that the wavelengths of all the photons get stretched as they travel through the exanding space. The CMB corresponded to a temperature of around 3000 Kelvin at the time of "last scattering", i.e. the "cosmic photosphere", which corresponds to a redshift factor of about 1100. This means that we observe the CMB today as a blackbody which is about 1100 times cooler, meaning about 2.73K.
suppose that the universe will expand forever because of hubbles law.
what will eventually become of the microwave background radiation???
Submitted by NONIKALS42"AT"aol.com 5/07
It will simply continue to cool, i.e. the wavelengths will continue to stretch, so that the peak of the spectrum moves into the radio regime, and then further and further into the long wavelength radio waveband. This will make it harder and harder to detect (assuming that we're talking about billions of years into the future!). So in some sense we live at a special time when it's relatively easy to use the CMB to find out about the Universe!
Why does the CMB has blackbody spectrum?
Submitted by eozmelek@su.sabanciuniv.edu 5/07
That's a simple question to answer!
The CMB photons come from a time when the Universe was very much hotter and denser than it is now - so that the photons were created in "thermal equilibrium". This means they could be described as a distribution of particles with one temperature, i.e. they had the blackbody spectrum when they were born. As the Universe expands the blackbody spectrum keeps its shape, with all the photons losing energy together, so that the temperature of the blackbody decreases with time. The blackbody shape is preserved, even although the photons stopped strongly interacting long ago.
how do we know that
cmb occurred around 380000 years after the Big Bang, and why has its
state not perceptibly changed?
Submitted by randshindery"AT"yahoo.com 6/07
What we know is that the CMB sky that we observe is made of photons which last interacted with matter at about that epoch - we call this the "last scattering surface". We know that the temperature of the CMB photons is decreasing as the Universe expands, and we know the evolution of that expansion pretty well, since we now have reasonably good estimates for the present expension rate, plus the densities of ordinary matter, dark matter and dark energy. The "last scattering epoch" is determined by the time when the matter (mostly hydrogen) went from being ionized (because it was so hot) to being neutral (once it was cool enough). When we put together the dynamics of the expanding Universe, plus the estimates of the cosmological parameters, plus the physics of hydrogen atoms, we come out with a pretty robust determination of this epoch, which is around 380,000 years.
I'm not sure what you mean by asking why the CMB has "not perceptibly changed". The photons interact very little with neutral matter, and so we're simply seeing back to the time when the photons were last scattering strongly. This is just the same reason that we see the surface ("photosphere") of the Sun, rather than some closer or deeper surface.
if the universe continues to expand forever, what will eventually become of
the cosmic background radiation?
Submitted by joohyun.lee@yale.edu 7/07
That's a great question! Strangely enough I've just written a paper on this topic, along with my colleagues Jim Zibin and Adam Moss. So you can read the technical answer to your question here.
The short answer is that the temperature continues to fall, while the features on the CMB sky change in various ways, depending of course on whether the future continues to be dominated by the Dark Energy.
I understand that you wrote the review of CMB for PDG's Review of
Particle Physics chapter 23. You cited the value of CMB temperature as
2.725+/- 0.001 K from J. C. Mather, D. J. Fixsen, R. A. Shafer, C.
Mosier, and D. T. Wilkinson, Astrophys. J. 512, 511 (1999). But I surfed
this paper and found that they use 2.725+/- 0.002 K (95% confidence)
instead of +/-0.001K. I also noticed that you cited 0.001K as 1 sigma, so
my question is
Where did you find the data and can you give me a reference? Thanks
Richard Loogn
Submitted by richard.loogn"AT"gmail.com 7/07
The Mather, et al. 1999 paper is curently the best study on the CMB temperature obtainable from FIRAS. But unfortunately it's not 100% clear about what temperature to use! I think they never really thought that people would be looking for a place to cite for a better temperature measurement than the older FIRAS one. So the paper doesn't make the size of the uncertainty very clear. The reason of course is that it's dominated by systematic error, so it's nothing like Gaussian. What they quote is something like a 95% confidence limit. For Gaussian errors this is +/-2sigma. So 1sigma is half of 0.002, which is 0.001. I explicitly asked Dale Fixsen if that was what I should use, and he said if I insisted on a 1sigma error bar, then that's the best he could suggest!
What experimental evidence do we have that the CMB fills the entire
universe as required by theory?
Submitted by vorleons"AT"hotmail.com 7/07
I don't think this is "required by theory". The ubiquity of the CMB is what drives the theoretical picture (not the other way around).
The CMB is observed to be very close to isotropic, i.e. the same in every direction. Since CMB photons travel at the speed of light, then it would take an extremely controived universe to only have CMB photons arriving at us here and now from every direction, without having them everywhere else too! In fact the tiny amplitude CMB anisotropies have a pattern which constrains details of the cosmological model - and part of that is the need for radiation which fills the Universe and which dominated the total energy density at early times. I can't think of any way of avoiding having CMB photons everywhere.
There's a question that arises if you consider the CMB in the context
of thermodynamics:
The energy of a "photon gas" - Bose gas with zero chemical potential -
is a constant times T^4 times the volume. If T scales like 1/R, and V
scales like R, the total energy decreases like 1/R. If the CMB is a
photon gas, the expansion is actually isentropic (V*T^3 = const), or
reversibly adiabatic.
The question is where does this energy go? It has to be work done by
the gas expanding - but against what? It isn't interacting with anything
since the time of decoupling.
I should add that the "classical" assumptions - photons in a container
with volume V and temp T - don't necessarily apply to the CMB. There is
no container and, since the CMB doesn't interact with anything since
recombination, the numer of photons is constant. But if it's a dilute
Bose gas with a nonzero chemical potential, the spectrum isn't black
body.
Submitted jfjanak"AT"verizon.net by 8/07
This is a good question, which shows that you've been thinking hard!
There are several answers to similar questions already on this page. The reassurance that everything must be OK, comes from the fact that General Relativity (the theoretical cornerstone for our models of the large-scale behaviour of the Universe) manifestly conserves energy, at least locally. So if I consider any small volume of the Universe, then the energy "lost" from the CMB goes into "work done" in the expansion (since there's a pressure and a changing volume, then there must be "PdV work").
But you also raise the issue of how to regard the Universe, since it isn't really a closed system, except that in a sense it's the most closed system there is (since it is in fact everything!). So one can get into knots trying to think about the "total energy" in the Universe. But the picture we have of simple homogeneous spaces means that every bit of the Universe is (on average) the same as every other bit - so that tells you that the best way to think about the Universe is just to consider any little bit of it, and the same will apply to all the other bits.
Since we have moved from the Big Bang much more slowly than any radiation
given off at that time, why is there still CMB present in the universe?
(It ought to have outpaced the growth of the universe immediately and
disappeared into the void that the universe is expanding into.)
Submitted by bobjt"AT"talktalk.net 8/07
This is the most asked question about the CMB!
I encourage you to seek out many other answers on this page. But the short answer is that we haven't "moved from the Big Bang" at all, and that you have a mental picture which has to change before you'll be able to come to grips with this question.
The Big Bang happened everywhere. There are distant parts of the Universe which are right now detecting the CMB photons that our region of space gave off at very early times. If you can understand that, then you're a long way towards getting the right image for the expanding Universe that we live in.
Is it fair to say that today's microwave background is the redshifted
version of what were originally gamma rays?
That is, that the Big Bang produced gamma rays which filled the small
early universe, and that expansion caused these original gamma rays to be
converted to microwaves?
Submitted by mdrnhart"AT"yahoo.com 8/07
That's right! Today's CMB photons were once much higher energy gamma-rays. They've been redshifted down to lower energy as they travelled through the expanding Universe.
The second part of your statement is perhaps not as clearly correct, however. The early Universe wasn't "small". You should think of it as being very very big (even at early times) - but always expanding. So those early gamma-rays were everywhere (and moving at the speed of light in random directions from each point) - with the resulting CMB photons being everywhere today.
Several hundred years after the Big Bang the photons were decoupled
from the matter. Let us consider N photons that decoupled at that time and
follow them during billions of years until they arrive to our detectors.
The temperature was much higher than it is today, thus each of these
photons had higher energy. They have traveled in the Universe without
interaction for several billion years (thus they did not scatter, they
were not absorbed etc.). Finally they arrive to our detectors. However,
their energy is much lower now than it was earlier. WHERE DID THIS ENERGY
DISAPPEAR, if they had no interaction with anything? Does this mean that
in an expanding Universe the energy conservation does not hold anymore?
Generalising: does this mean that the total energy of the radiation in the
Universe is much lower now than it was when the radiation has decoupled?
(Not considering obviously the radiation coming from the stars.)
Submitted by sukosd"AT"reak.bme.hu 11/07
This question is answered several times on this page already! The short answer is that the energy per unit volume is conserved, since there is a "work done" contribution due to the expansion. In other words one could alternatively ask: "Since there's a pressure coming from the photons, and also the volume is changing in an expanding universe, then where do I get the energy from to cause the expansion?" The answer to that would be: "from the fact that the photons are losing energy!"
In certain books the "cooling down" of the CMB is explained as a
consequence of a "scaling" in the expanding Universe. They say, that
because of the expansion of space every distance is scaled by an universal
factor. Since the wavelength is also a distance-like quantity, it is also
scaled, causing the whole CMB to shift toward larger wavelengths. My
question is: if we take serious that EVERY distance-like quantity is
scaled, then for example the radius of the H-atom (and many other physical
quantities) should scale as well, since it is also distance-like! This is
probably nonsense, since the radius of the H-atom is determined by
fundamental contants (e, h, c, electron mass, etc.). If it scales, then
either these fundamental contants should scale somehow as well, or the
physical laws should change with time... I think that none of these could
be accepted.
Submitted by sukosd"AT"reak.bme.hu 11/07
This is an excellent question! It shows the sort of thing that can happen when one gives a relatively simplified answer to a basic question, but the questioner then goes on to think about a deeper question, which shows the limitations of the pat answer!
It's really space that's expanding, not the things within that space. So atoms etc. are not getting stretched. However, photons are kind of special, because they are purely energy, being defined only by their wavelength. The rest mass of a particle (for example) isn't changed at all by the expansion of the Universe, but photons have no rest mass. When they travel through space their wavelengths really do get stretched, while the properties of more ordinary particles do not.
If that still sounds a bit suspicious, then the real answer is that there's a rigorous mathematical picture underlying all of this, which is General Relativity. And when you follow photon trajectories in an expanding medium within General Relativity, you do indeed find that they lose energy. This is of course confirmed empirically by Hubble's law, which is just that the redshift of a distant object comes from the fact that this "universal factor" was smaller when the photons left the source.
If the wavelength of the photons of the CMB radiation were
"redshifted" during the years they travel, it is plausible that the same
redshift occurs to the photons emitted by distant stars. This redshift
does NOT depend on the actual velocity of the star, since it depends only
on the time the photon travels until it hits our detector. Question: is
THIS universal redshift taken into account (deduced) when determining the
velocities of distant stars? With other words: when we determine Hubble's
constant, is this universal redshift of photons taken into consideration?
Submitted by sukosd"AT"reak.bme.hu 11/07
The redshift measured for a specific source of radiation has several distinct contributions. Physically you can think of the main "Hubble flow" redshift, which comes from the ratio of the universal "scale factor" between the time of emission and observation of the photons. But secondly there's a contribution coming from the "peculiar velocity" of the source relative to a smoothly expanding Universe. And thirdly there's the peculiar motion of the observer, which includes the rotation of the Earth, orbit of the Earth around the Sun, etc.
See in this way, I think it's obvious that there has to be these additional "Doppler" redshift contributions. That's because the answer you get must depend on whether you make a correction to a frame in which the Earth isn't rotating (a small, but measurable effect), then there's the 30 km/s motion of the Earth around the Sun (so that normally redshifts are expressed in a "heliocentric frame"), and for extragalactic objects one must decide whether to remove the Sun's orbit around the Galaxy, the Galaxy's motion relative to nearby galaxies etc.
Assuming that the Universe will expand forever, what will eventually
become of the CMB?
Submitted by Lcep72"AT"aol.com 12/07
It will continue to cool as the wavelengths stretch, and so will become the CRB (Cosmic Radio Background).
My question is that whether Big
bang theory has any thing against the assumption that there 'universe of
anti-matter'? and if at all an anti-universe exists, is there possibility
of CBR? if so, what can be its nature; red shift or blue shift?
Submitted by saumya_mohapatra"AT"yahoo.co.in 12/07
I'm not sure I fully understand the question - but let me try to answer it anyway!
Ever since anti-matter was discovered there have been suggestions that maybe there are parts of the Universe filled with anti-matter, just as our part is filled with matter.
There are strong constraints on such ideas, particularly when you realise that there's nowhere in the Universe which is truly empty (e.g. the vast intercluster medium pervades all the space between galaxies, with a density of hydrogen and helium which is only a thousand or so times less dense than in clusters of galaxies) - so there are no "voids" to separate the speculated regions of anti-matter from the regions of matter. That means there should be gamma-rays being formed where the regions meet - and we don't see anything like this.
Inventing deep voids just to separate these regions of matter and anti-matter sounds pretty contrived, and not much like the dynamical Universe we live in. The voids would have to be big enough not to have changed much in the age of the Universe. And if they were that big they'd strongly affect the CMB anisotropies on large angular scales - which again we don't see.
So the idea that there are anti-worlds etc. out there, although it has a certainly science-fiction-type appeal, is not something which appears to happen in the real Universe!
In fact there's a big puzzle from the "hot Big Bang" picture, which is why the Universe chose to be mainly matter, rather than a balance of matter and anti-matter - but that's another question that I'll leave for another time!
I was wondering if you know the mass density of radiation from the CMB with
temperature 2.73K.
Any information on how to calculate this would be much appreciated.
Submitted by thomas.carpy2"AT"mail.dcu.ie 01/08
This sounds like someone asking for help on a homework question! I'm afraid I have a very strict rule about not doing other people's homework without getting paid!
There's an old joke about how you use a barometer to tell the height of a building. Along those lines, the answer to this question is: "Find the owner of the Universe and tell him that you'll give him a very nice Cosmic Microwave Background of temperature 2.73K if he'll tell you its mass density".
...However, I personally am unconvinced that CMB came from the Big Bang itself
(please understand that I am not necessarily questioning the big bang
itself...I'm just questioning CMB as EVIDENCE of the Big Bang). To me, CMB
looks like just another manifestation of Dark Energy! In fact, I think that if
Dark Energy had been discovered before CMB, then CMB never would have been
attributed to the Big Bang. You have to admit it, the two (CMB and Dark Energy)
seem quite similar, at least in there pervasiveness throughout the universe and
the timescale of their existence (I'll talk more about the latter shortly).
[abridged]
Submitted by chadswhite"AT"juno.com 01/08
Actually the CMB and the Dark Energy are physically completely different. The CMB is composed of particles moving at the speed of light, which have a significant positive pressure. This turns out to mean that in a Universe with an expanding "scale factor" (i.e. the Universe in which we appear to live) the energy density of the CMB decreases as the 4th power of the scale factor. The Dark Energy, on the other hand, appears to be similar to a "cosmological constant" or pure "vacuum energy". This has a negative pressure, which means that in an expanding Universe the energy density doesn't change at all. This Dark Energy behaves as a very bizarre sort of stuff, entirely different from what we normally think of as "matter" or "radiation". Hence this new name was coined, to emphasize the distinction.
Another major difference is that although you can "squeeze" the CMB (so that bits of the Universe are a little bit hotter or colder than other bits), you can't squeeze the Dark Energy (or at least not very much) - it's pretty much a uniform fluid that fills the Universe.
Another issue that makes me doubt the link between CMB and the Big Bang is the
following: According to current theory, the microwaves of CMB would have been
generated ONLY during a certain early phase of the Big Bang. Why then are we
STILL getting hit by the microwaves? Is it just a big coincidence that we happen
to be alive during the (cosmologically) brief period in which the radiation
generated from this early event hit the earth? If we had lived a billion years
ago, would this burst of radiation not yet have arrived? If the human species
still exists in a billion years, will the burst be over?
Submitted by chadswhite"AT"juno.com 01/08
You've just posed the single most asked question about the CMB! It occurs in several different forms on this page, and so I encourage you to look for the answers.
The fundamental resolution for what you are thinking is that your mental image is wrong. The "Big Bang" is not a specific place, but is everywhere!
I would
just like to ask a few questions that have been puzzling me, and i need
to answer for an assignment could you help me please?
. At the point of recombination how much had the CMBR deteriorated from
its original gamma rays?
. Is it possible to calculate the rate of degridation from the CMBR now
and hence determine when it might end?
[abridged]
Submitted by onephatwookie"AT"hotmail.com 01/08
I try not to do people's homework for them!
There should be plenty of information on this page (and others on the internet) to help answers those sorts of questions.
I just selected out a couple that were posed here, since I don't really understand them - but on the other hand they might still be interesting to answer!
It's true that CMB photons were once gamma-rays, of arbitarily high energy. They "formed" (in the sense of when they stopped being significantly created and destroyed in particle interactions) when the Universe was about 1 year old. So I guess you could consider this to be when the photons that we detect today came into existence. Then you could figure out the temperature at that time, and hence the ratio of typical photon energies today compared with back then.
But the photons continued to scatter off the matter (although not changing energy very much) until the "last-scattering epoch" which was at an age of about 400,000 years. The temperature at that time was about 3000 Kelvin and the photons at that point were optical (or mildly infrared, with typical wavelengths of about 1 micron). You could also calculate the factor by which the photons have lost energy since that time, and the answer is around 1000 (which is the redshift of the last-scattering epoch).
As for what will happen in the future, well the CMB photons will continue to lose energy forever. Or perhaps, in a vacuum-dominated model, they'll eventually have wavelengths around the size of the observable Universe, and hence the concept of a CMB temperature will eventually lose meaning. But that's quite a long way off, when they've reduced in energy by another factor of around 1028 - and who knows what else might have happened by then!
They say that the total mass-energy density in the universe is about 9.9 x 10-30
g/cm3. According to the following link, it breaks down thus: 4% Atoms, 23% Cold
Dark Matter, 73% Dark Energy.
http://map.gsfc.nasa.gov/m_uni/uni_101matter.html
My question is: Is the CMB even considered in this break down? If so, in which
category does it belong? If not, why is the CMB not considered in the total
energy density of the universe?
Submitted by chadswhite"AT"juno.com 02/08
When you work out the numbers, a 2.725 Kelvin thermal spectrum of photons corresponds to an energy density which is quite negligible compared with the energy density in matter and in dark energy.
The CMB contribution to that budget is about one hundredth of one percent, i.e. a fraction of around 10-4.
However, in earlier stages of the history of the Universe things were quite different. That's because in an expanding Universe the ratio of energy densities of radiation and matter decreases with time. So at earlier times the photons were more important. In fact if you go back early enough the photons made a bigger contribution than everything else, and we call this the "radiation-dominated" phase. This occurs when the Universe is younger than about 100,000 years.
when we look at CBR, are we seeing microwaves that have been
travelling TOWARDS us since the moment the universe stopped being opaque,
or are we picking up microwaves that are bouncing around (and have been
bouncing around since the universe stopped being opaque) the same "chunk"
of space that we now inhabit, i.e. they really are BACKGROUND and have
simply expanded along with us as our part of the universe expanded?
Submitted by andy_kovacs"AT"yahoo.co.uk 02/08
It's the former. We are seeing microwaves which have travelled straight towards us since they last scattered at this opaque era (the "last scatttering surface"). We're seeing the early Universe in all directions, because space has always been really, really big!
Hi...I was just wondering if you knew what the relationship is between the CMB
and why a machine can never run at 100% efficiency.
Submitted by CYVERIA1"AT"MOUNTAINCABLE.NET 03/08
I'm not sure there's any direct connection. They are both related to the laws of thermodynamics - but that's about it.
Unless someone else ses that I'm missing something here?
[follow-up question]
......the answer was in the laws of thermodynamics.
At one point the article spoke of heat loss, etc. It went on to say 100%
machine efficiency would have to be at absolute zero. My understanding of 0
degrees Kelvin is that it can never be achieved because of the 2.7 degrees
Kelvin from the CMB.
Submitted by CYBERIA1"AT"MOUNTAINCABLE.NET 04/08
It is possible to reach temperatures below that of the CMB. It's done all the time in low temperature laboratories, and in fact the detectors used to study the CMB are usually cooled to well below 2.7 Kelvin!
Of course it isn't easy to reach such low temperatures, requiring lots of energy (and increased entropy, and all those other good thermodynamics ideas!). It would be genuinely hard to do it for very long, since the CMB is everywhere, and so if you wait long enough (in laboratory units, but certainly short on a cosmological scale!) your experimental system will tend to reach equilibrium with the CMB.
i have to write a small esay about Cosmic Microwave Background Radiation
and the question that i have the answer is what is it. so can u tell me
in general terms what is it?
Submitted by antoine_washington1@yahoo.com 04/08
It's a background of radiation that comes from the Cosmos!
But seriously, you can find the answer by reading the basic page which is above this one, i.e. here, and by reading answers on this very page.
Hi, I read your FAQ on the CMB online and i had a couple questions. so
lately i've been trying to understand this theory. I understand that we
can sense this uniform background radiation in uniform all across the
universe. And this radiation is evidence of the early universe, but how
exactly is it evidence of the early universe? we know the universe is
expanding from the red shift in galaxies. But i guess i'm just confused
on how exactly the CMB confirms the big bang. in simple terms if you
could just fill that info in it would be appreciated. and the radiation
is at 2.73 kelvin today (does the 2.73 represent what it is today or many
eons ago?), how does that tell us of the early universe? that the
universe is cooling because it is expanding?
Submitted by tbmcquade@gmail.com@yahoo.com 04/08
The basic fact is that the CMB has a spectrum (i.e. brightness as a function of wavelength) which is extremely accurately described by a "blackbody" shape (i.e. the shape that a body has which has a single temperature). The only explanation that we have for this is that the radiaton came from a time when the whole Universe was in good "thermal equilibrium" - a situation which you get very naturally if the Universe used to be very much hotter and denser. The alternative, "obvious" source of the CMB would be some relatively local cool material which is distributed more or less uniformly - however, there's no way to do this without getting emission or absorption features, so all such ideas were ruled at least 30 years ago.
On top of that, we now have precisely measured CMB anisotropies, covering a wide range of angular scales. These are very well fit with a model of evolving density perturbations in a universe which starts off hot and expanding. So it is very hard to avoid the conclusion that the Universe was once very hot and that our basic understanding of its evolution is in good shape (although of course, there are still many unaswered questions).
In an expanding Universe which contains radiation, it is expected that the radiation is cooling with time, and hence was hotter at earlier times. So the CMB fits in very well with the expanding Universe picture, or what is often referred to as the "Hot Big Bang picture".
can't seem to find if CMB is flat , ie freq v. amplitude, or decreases with freq
or if it has a peak
at some freq. What I'd love to see is noise temp v freq, so that if I had a
perfect mw antenna,
perfect lna with 0db NF and both flat from say 50MHZ to 10 GHZ, what would I see
looking
at it wqith a perfect spec an with differebt IF bandwidths.
Submitted by patr@tac.com.au 05/08
The CMB spectrum is a pretty much perfect "blackbody spectrum", with a low frequency slope, a peak, and then a high frequency exponential fall-off. You can look up the function in any basic physics textbook (or on the internet).
The precise form will depend on the units you are using. If you are using "noise temperature" in the radio (long wavelength) part of the CMB spectrum, then noise temperature is constant with frequency.
If I look at a plot of the Hubble data, and want to include the microwave
background as data, I have to extend the x-axis out to 14 billion
parsecs. If I then extrapolate the linear Hubble trend to 14 billion
parsecs and read the recession velocity from the y axis, I read 1,040,000
km/sec. This is about 1/3 the velocity of light. Is this correct? Before
I conducted the exercise, I was expecting that the microwave recession
velocity would be very close to the velocity of light (not equal to c
because then the redshift would be infinite). If this estimate is
correct, is there some way to understand why this number and not some
other. Does it make sense to think of the source of the CMB to be
receding same as any other distant source?
Submitted by Dave.Kennedy"AT"Inteq.com 06/08
If you try to interpret the very distant Universe in terms of a recession velocity, you quickly get in trouble. This is because we're dealing here with General (not Special) Relativity, and you also have to take into account that as you look at distant objects you're looking back in time (so it becomes unclear when you are measuring the speed!). If you do the full calculation within the expanding Universe model, then you find that the CMB photons were indeed emitted from a surface which is expanding away from us at close to the speed of light.
However, things are actually much simpler if looked at in terms of expansion rather than velocity. The Universe is expanding uniformly, which means at earlier times everything was closer together than they are now. The CMB photons were last scattered when this "scale factor" was about 0.001, meaning that the photons have been redshifted by a factor of about 1000. That's why we observe the "hot" early Universe in cool microwaves.
Does the cosmic background radiation permeate,travel through the
planets or just surround it ?
Submitted by info"AT"drnabilhassan.org.uk 06/08
The planets (and stars for that matter) are opaque to most radiation. So just as you can't see stars through the Moon, you can't see the CMB photons either. The planets (satellites, asteroids, etc.) also emit microwave radiation of their own, however. This is because they are glowing at some fairly cool temperature, so that they give off radiation which typically peaks in the far-infrared part of the spectrum. These bodies are actually much brighter than the CMB, and that can make them useful as standard sources of radiation which can be used to calibrate CMB experiments.
I am also a bit puzzled about the fact that the CMB is centered on the 3K
wavelength. This is said to translate into a radiation that originates from the
universe when it had a temperature of 3000K. As the universe cooled is seems to
me that there ought to be radiation originating at every degree lower than
3000K, e.g. at 2900, 2800, 2700, etc. degrees. With the redshift caused by the
expansion this should translate into something like 2.9, 2.8, 2.7 etc K. That
is, there ought to be a continuous CMB at wavelengths larger than the 3K
wavelength as I see it. Why isn't that the case?
Submitted by carl"AT"ullerup.com 07/08
This is because the CMB photons are last scattered at redshifts around 1000, when the temeprature was about 3000K. After that the photons travel freely towards us, stretching in the expanding Universe. So we are seeing back to this early time of intense scattering (between radiation and matter). We can't see radiation coming from, say, redshift z=100 when the temperature was about 300K, because there was no interaction with matter back then. Although of course we can if we like consider the CMB photons as being 300K radiation from z=100 or 30K radiation from z=10, or whatever, since it's all equivalent to seeing 3K radiation today. The point is that the radiation only last scattered at z=1000, and so that's the surface around us where we see the matter distribution being imprinted on the CMB anisotropies.
I have no idea ?how this may sound to you ?or how unusual this may be,
but I believe I can see the cosmic microwave background. ?For ?as long
as I can remember I've seen static everywhere, all of the time. ?A few
years ago I discovered that other people didn't see this static, so I
went to eye doctors to out if there may be a problem ?with my vision. ?I
am near-sighted, but I see the static better with my contacts in and
there was ?no sign of any other problem. ?I a feeling that this may be
of interest to some one. ?I don't really know who to contact. ?I would
like to find out more about this. ?Is it even possible that I could be
seeing CMB?
Submitted by brooke_simpson27"AT"yahoo.com 07/08
I'm sure you are experiencing some sort of sensation in your vision, but it isn't possible that this is the CMB. The energies involved are dramatically lower (more than a factor of 1000) than what is required to excite the optical receptors in our eyes.
Human vision is a complicated thing, and not something I'm an expert on! However, I would suggest that you try to find more information on the internet to learn about how vision works. Hopefully you'll find something that explains what you may be experiencing.
why is it no one has thought of cosmic B.R. as an alternative sourse of
energy
Submitted by info"AT"drnabilhassan.org.uk 09/08
Although the CMB is the dominant photon background in the Universe, it is completely negligible by terrestrial standards. We live in a very special part of the Universe! We are in a very overdense galaxy, very close to a bright star, on a rocky planet, surrounded by gases, etc. The CMB is the same here as it is everywhere, but there are spectacularly higher local sources of energy (specifically coming from the Sun or from radioactivity from previous generations of stars).
Was CMBR temperature 2.725 K calculated for the local potential where CMB was
investigated (taking into account CMBR blueshift due to potential wells of the
Earth, solar system and the Galaxy as a whole) or evaluated in homogeneous
space? In other words, what would be CMBR temperature measured in a place where
it is possible to neglect a curvature of space? As within the Galaxy the
average density is around a million times the average density of the Universe,
the original small fluctuations of density-temperature became huge (while
matter have clumped) and a difference between these temperatures expect to be
essential.
Submitted by astronet"AT"yandex.ru 09/08
Although the local density is very much higher than for average parts of the Universe, the gravitational potential (or equivalently the curvature of space) is not very different. You need to be a black hole to have a genuinely large amount of curvature (and hence a large "gravitational redshift"). So the CMB temperature measured at the Earth only differs from the "empty Universe" value in about the 8th decimal place.
You say that the density of the cosmic microwave background radiation is being
diluted as the universe expands. How do you know this? Is there some
experimental data that shows that this radiation is becoming less intense over
time?
Submitted by chadswhite"AT"juno.com 10/08
It's really required in an expanding Universe. And several things would go completely wrong (e.g. fitting the CMB anisotropies, measuring the Sunyaev-Zel'dovich effect) if it were not true.
But there's also some direct proof, which comes from making estimates of the CMB temperature in very distant gas clouds (i.e. at high redshift, z, where the CMB temperature should be (1+z) times higher). These estimates can be made from looking at the ratios of the strengths of particularly molecular lines in the gas clouds. This gives the local "excitation temperature", which can't really be lower than the CMB temperature - hence the lower envelope of these measurements should track 2.725 × (1+z)Kelvin, which is indeed found to be the case.
I don't mean to beat this topic to death, but it is important for me to
understand this better.
First, let me see if I understand the direct evidence. You're saying that they
have measured the lowest temperature of distant galaxies, and it came out to be
about 2.725 K? Is this what you're saying?
Also, I don't understand how the interaction of high energy electrons with the
CMB (Sunyaev-Zel'dovich effect) shows that the intensity of the CMB is getting
weaker with time...
Lastly, how does anisotropies of the CMB show that the CMB is being diluted?
Submitted by chadswhite"AT"juno.com 10/08
Temperatures measured in very distant galaxies are consistent with 2.725 × (1+z)Kelvin, not with 2.725 Kelvin. So for example in a galaxy at z=2 you see temperatures around 10 Kelvin.
The "Sunyaev-Zel'dovich effect" is like a "hole" in the CMB caused by scattering through the hot gas in clusters of galaxies. The spectral shape of this signal is what you expect if the gas is scattering CMB photons which have a temperature of 2.725 × (1+z)Kelvin for a cluster at redshift z.
The detailed "power spectrum" of CMB anisotropies is very well explained by a model having about 6 parameters within the "hot Big Bang" framework, meaning that the Universe used to be hotter and the CMB has been cooling. This is a crucial part of the whole picture, and there's no way to make sense of the CMB anisotropies without the "last scattering surface" at redshift around 1000.
I am doing an investigation on how CBMR supports the Big Bang theory and
disproves the Steady State theory. I need to see what mathematical proofs
support one theory but not the other. Therefore in terms of mathematical
resources (not theoretical, I have read to much theoretical) , do you have
any recommendations on credible sources?
Submitted by ebustos23"AT"gmail.com 11/08
There are several textbooks available, which cover this material at different levels (depending on how much physics and mathematics background you already have). However, the steady state theory is really rather an old-fashioned idea at this point! It was so definitively ruled out several decades ago that I don't think it features very much in the newer books (I checked a few of my favourite recent texts and they mention it only briefly in a historical introduction). So you may be best going back to older books, particularly those published in the 1970s or 1980s. I should also point out that the CMB is only a small part in the story of why the steady state model fell out of favour when it was confronted with concrete observational evidence.
I have a question concerning our conception of space in the big
bang theory. Are we entitled to ask this question: where did the big bang
happen? If it happened at a certain point in the universe far from us, how
come the CMB is coming from all directions? and how come the earth reached its
current position before the CMB photons reached it?
Submitted by T.elsayed"AT"ThPhys.Uni-Heidelberg.de 12/08
Yes you are entitled to ask that question!
The answer is that the "Big Bang" happened everywhere at once. If you can get your head round that, then you've come a long way towards understanding how the Universe works! And you can find more detailed answers on this page.
Another question regarding the CMB photons, if their frequency has
decreased from the instant of their creation till now due to the expansion
of the universe, where did their energy difference go?
Submitted by T.elsayed"AT"ThPhys.Uni-Heidelberg.de 12/08
It goes into exapnding the Universe, which takes energy!
What causes us to be able to see the CMB. What material is it reflecting
off of ?
Submitted by Kenneth.C.Herr"AT"aero.org 12/08
The CMB photons are scattering off charged particles which existed in the hot early phases of the Universe. We are seeing them when they last scattered off this plasma about 13 billion years ago!
I am aware of the cosmological principle,but if all aroud us at approx 14
billion light years is the cmb ;doesnt that infer we are in the middle.Forgive a
layman Im sure theres a reason this is so,but I had to ask .Its something
Im not getting
Submitted by Toonheid"AT"aol.com 12/08
We're in the middle of our own "Observable Universe"!
We see the CMB photons which are reaching us right now from all directions, having travelled for (most of) the age of the Universe. Other observers will be seeing other parts of the early Universe, and will be at the centres of their own patches.
Is the strength of the microwaves now constant or still diminishing??
Submitted by jawepret"AT"blueyonder.co.uk 01/09
The CMB is still diluting as the Universe expands. It will continue to cool forever! Although the timescale for this variation is very, very long, so the change in the CMB temperature over your lifetime would only show up in about the 8th decimal place.
Where can I find the audio or sound of the Cosmic Microwave Background
Radiation?
Submitted by wynnwolfe"AT"pacbell.net 04/09
Of course the CMB isn't sound, it's a form of low energy electromagnetic radiation. However, it can be represented as sound, and this has been done in a few different ways, which are pointed out elsewhere on this page.
My question is: with the CMB sitting out there at 13.7 LY, all we can see
or experience is its translucent image. If this can be spoken of as
the outer limits of our ability to see "the beginning", can a case be made that
it too is now "clear" in real time? If we could see through this CMB what
would it show us?
Submitted by stephenbierce"AT"yahoo.com 04/09
That is of course a very hypothetical question!
The answer depends on which bits of physics you're willing to push aside, and which bits you're happy to keep. So I don't have a specific answer.
If the question is something like "given that we see the CMB sky pretty much as a snapshot at 380,000 years after the Big Bang, what would it have looked like if scattering was a bit less and we saw it instead at some earlier epoch, like 100,000 years after the Big Bang? or 1,000 years?"
The answer to this more specific questions is that if the CMB "last scattering surface" was (for some reason) a bit earlier, then obviously the CMB sky wouldn't look drastically different. The pattern of anisotropies would have a different dependence on angular scale, that's all.
If you're imagining seeing back to much earlier times, then the question is much harder to answer! That's because the physics you'd have to change to affect the transparency of the CMB would also affect some of the other things going on, like the oscillating sound waves, or potentially things like the coupling of neutrinos, the balance between matter and antimatter, the details of nucleosynthesis, etc.
The CMB photons that we see were created (although there's some ambiguity here over precisely what is meant by "created") something like a year after the Big Bang. So in a sense we're seeing the Universe as it was at about that time, except for photon trajectories being scattered.
The fluctuations that we see on the CMB sky were probably generated much earlier than this. So there's also a sense in which we're seeing conditions that existed when the Universe was only a fraction of a second old. If we ever manage to probe primordial gravity waves, then we can claim to be seeing back to an epoch when the Universe was "opaque" to gravitational radiation, which is this same very early time (perhaps when the Universe was inflating).
I have a couple of questions about the Cosmic Microwave Background Radiation
Experiment.
1.) What is the Hypothesis of the Experiment? ... [abridged]
Submitted by j.torrez44"AT"yahoo.com 06/09
Although CMB instruments are "experiments", they are a little different from the traditional "scientific method" type of experiment. The usual model we have for how science progresses is that one designs an experiment to test a hypothesis, refines the hypothesis, designs new experiments, etc. But astronomy (i.e. the study of the heavens) is a bit different from this (in fact all of science is a bit different from the simplistic "scientific method" - and a good thing too, otherwise it would be very boring!). In astronomy you can't go and visit the objects you are studying, and so you can't change them to see what will happen. You just observe what you can and then draw inferences.
CMB experiments are motivated by a desire to learn about the Universe on the largest accessible scales. There is a fairly simple model which describes the main features of the Universe, and that model is constantly being tested by such experiments. More importantly though (given that the basic model seems to work quite well) the parameters of that model are being fitted using the CMB data. If there is no good fit, then that will tell us that we need to adapt the model - which is how progress is made in understanding how the Universe works.
Is there a way to generate a plot of background temperature vs time from last
scattering to now? Or is there such a plot already made that I could look at?
Submitted by edweinb"AT"sbcglobal.net 06/09
The CMB temperature is just inversely proportional to the "scale factor". In terms of redshift the relationship is simply T(z)=T0 (1+z), where T0 is the temperature today. Epochs in the early Universe can be described by the redshift that they would be observed at by us - so we live at redshift zero and the very earliest moments have very high redshifts.
The complication with plotting the CMB temperature versus time is that the relationship between time and redshift depends in detail on the cosmological model. If you specify exactly how much dark matter, dark energy etc. you have, and the precise value for the expansion rate today, then the relationship between redshift and time is calculable. But if you decided you preferred a different amount of dark matter (for example), then the relationship would be a bit different. For a Universe with multiple components making up its density, like the Universe we appear to live in, the z to t conversion comes from doing a numerical integral. So there isn't a simple formula that can be written down here.
However, here's a plot for something close to the currennt best-buy cosmological model. You should be able to combine this with the value of the CMB temperature today to figure out what the CMB temperature was at different times in the past.
I have question about one of the Horizon problem, which some boks state it as
most crucial problems of the this theory.
As I have understood this problem, it can be stated in two sentences:
1- There are some points in the Universe which are not causally co-related
2- What we see in the CMB is that these points have the same temperature, and in
the explanation of this "same temperature" , we say that these points had been
in thermal equilibrium at the time of the CMB photons formation, and so these
points should have been causally related.
So, we see a kind of contradiction in the above sentences, and this is the
horizon problem.
What I can not figure out is that why do we need to say that these point had
been in thermal equilibrium? These points had started from the same initial
conditions and so they should have the same temperature without being in thermal
equilibrium themselves.
Submitted by anariman"AT"interchange.ubc.ca 06/09
Remember that the Universe didn't start out as a "point", but has always been large! This matters for precisely the issue that you are trying to understand here. When you work through the business of causality (i.e. objects being within the light-crossing distance of each other in the age of the Universe), you find that the causally-connected distance always grows with time in the usual expanding Universe.
This observation is important - because it means that if two points are only just becoming causally connected today, then they can never have been causally connected in the past. Expansion of the Universe just isn't fast enough to beat the growing size of the light-travel distance.
Hence the opposite sides of the CMB sky, which even today aren't quite in causal contact with each other, were horribly out of contact the earlier and earlier you consider things.
There are 2 possible ways out of this dilemma. The first is to say "well, maybe the initial conditions were just set up in some acausal way, so that everywhere had the same temperature at some early time". But that kind of seems like giving up! Unless of course you have a good explanation for the magical process which achieves these early conditions.
But the second possibility is more promising. "All" you have to do is arrange for objects to fly apart faster than the speed of light, so that they start off within causal contact, but then get very far apart. This idea is called inflation, and it turns out to be a very promising idea for understanding what might have happened in the first tiny fraction of a second. As well as solving this "horizon problem", it also gives a fairly natural explanation for why there is any structure in the Universe at all, by stretching quantum fluctuations to become macroscopic perturbations in density!
I read of a study that shows the CMBR temperature 11
billion years ago was 9K. Assuming that the only mechanism for cooling of the
final scattering radiation is wavelength stretching due to expansion, I would
have expected the CMBR to be much higher. After only 1.7 billion years I would
have expected that the background would have still been visible glowing. What
am I missing here?
Submitted by edweinb"AT"sbcglobal.net 06/09
No, you have the timescales quite wrong. The CMB came out of the visible part of the spectrum at around the time of the "last scattering surface". This corresponds to a redshift of about 1000 and a time of about 400,000 years after the Big Bang.
Would the redshifting of the peak of the cosmic background do anything
interesting at various ages of the universe if it
matched an absorption line in some material like hydrogen or helium (or would
the peak be so weak that it would not
make so large a difference?) I mean that running recent history backwards the
peak would reach into the infrared at
sometime and cause things to be baked, no? [abridged]
Submitted by smkolins"AT"mac.com 07/09
The short answer is that any such effects are small enough to be almost negligible.
The longer answer is that if you care about the details, then there is some quite interesting physics associated with the interaction between the CMB and hydrogen and helium atoms as the Universe cools. The "recombination" of hydrogen and helium leads to weak (and broad) emission lines in the spectrum of the CMB. And the interaction between this spectrum and the energy levels in hydrogen and helium can even lead to some absorption features. I've written papers on this topic, as have several other people! A readable summary of recent work on this topic can be found here.
what are the best theories to date with what lies beyond the cmb?
Submitted by Electrodynamic"AT"hotmail.co.uk 07/09
We see the CMB photons coming from the "surface of last scattering", defined as the time when the Universe became transparent to these photons. At earlier times the atoms in the Universe were ionized, and ionized material interacts very strongly with photons. It's like trying to look into the Sun - you can only really see the surface layers, because it is too "optically thick" to see further.
The cosmic "last scattering surface" is at about an age of 380,000 years in the history of the Universe. Before that we have a very good picture of how the Universe had been expanding, getting cooler and less dense. This is usually called the "hot Big Bang model". It is very successful at explaining a great many observational facts about the Universe. However, it gets less an less clear as we try to ask about earlier and earlier times. One hope from the CMB is that we can detect the effect of gravitons as well as photons. The gravitons (or gravitational waves) only scatter at fantastically early times. And so if we can detect them (which is difficult although possible) we'll be "seeing" conditions in the Universe when it was perhaps less than a trillionth of a trillionth of a second old.
What is exactly is cosmic microwave background radiation is simple terms?
Submitted by bbsnsxo2"AT"hotmail.com 10/09
Read this page!
So what I do know is, that the existence of the CMB frame is not a problem
for general relativity, as the only thing that is special to it is, that the
CMB is uniformly distributed from this frame's point of fiew. Physics is
still the same fiewed from both, the CMB frame as well as from any other
frame one might choose.
The part I don't really understand yet is, that it is often said, that the
CMB frame defines a rest frame of the universe.
What exactly is meaned with "universe" in this statement?
(1) Is it the spacetime manifold itself? So would one really be able to tell
if he is moving with respect to space?? -- (what i doubt)
(2) Or is it the frame in witch all particles (including massles ones, like
the CMB-photons) are distributed in the most uniform way? So one would just
be able to say, if one is moving with respect to this frame, and not with
respect to space itself.
Submitted 11/09
The phrase "the CMB frame defines a rest frame for the Universe" is not really a meaningful statement! It is meant to simplify the situation for people who are first thinking about this topic. More sophisticated people will realise that it's not at all clear what it means (if anything!).
The correct picture is more like what you describe as number (2) in your question.
Can the CMB frame really be seen as a rest frame of all particles in the
universe - so for the CMB + all the matter and stuff that is flying arround.
My guess is: No, it can't. - I mean: The CMB is just one component of all the
stuff that was created. One cannot argue that the rest frame of this
component has to be the rest frame of the sum of all componetns as well.
So my guess is, that the CMB frame is really just the frame in that just the
CMB, and nothing else, is distributed uniformly. Not more and not less. So
in this case the grade "rest frame of the universe" would not be a really
good name to give to it at all.
Submitted 11/09
This seems quite perceptive to me, well done!
If you really want to read more on this kind of topic (at the kind of technical level) you could do worse than see a paper I wrote with Jim Zibin, which you can find here.
I've noticed something that I've never seen explained, and was hoping you could
shed some light on;
Fact 1: The Universe has an average temperature of 2.73 K.
Fact 2: Absolute zero is 0K = -273 deg. C.
So, the avg. temp. is exactlyB (-)100 times absolute zero. Is this a
coincidence, or is there a real connection between the two?
Submitted Andy Smith
You're not the first person to note this coincidence! See this page for several (crazy!) ideas involving CMB temperature numerology.
This is of course a coincidence. The CMB temperature is changing with time for one thing. And the numbers are actually 2.725 and 273.15, so not exactly a factor of 100 anyway.
how do they know the temperature of the microwave background radiation? Can the
temperature of a specific microwave wavelength be different temperatures. I
assume so but since temperature is a measure of a vibration of some sort and a
specific microwave photon has this temperature associated with it, what material
is it that is actually vibrating so we end up reporting a temperature?
Submitted rhelande@d.umn.edu 2/10
You're right that you can't measure the temperature of an individual photon. When a hot object emits photons, it is the distribution of wavelengths of the collection of photons which is determined by the temperature. Hence, if you can measure the spectrum of photons then you can determine the temperature.
The thing which is "actually vibrating" is the material in the whole of the early Universe! This is back at the time when it was very hot and ionized. Since that epoch each photon has simply travelled in a stright line, losing energy in the expanding space.
Background: 2005 NASA proposed a lunar radiation shield that is essentially
a set of carefully arranged highly charged (to "match" the radiation)
spheres to produce a repelling "forcefield" effect.
my question/thought is this (propulsion related) would it be possible to use
the CMBR as a "traction surface" for what would be essentially a tube lined
with rings of smaller sphere's that pass their opposite (to CMBR) charge
sequentially "down" the rings along the length of the tube? instead of
aiming to use this attraction field ONLY to "draw" CMBR into the tube like
air into a jet engine, aiming more "for tractor tracks on loose snow".
Submitted az.sanders"AT"yahoo.co.uk 2/10
I think you may be confusing the CMB with cosmic rays (at least for the "lunar shield" idea).
The energies involved in the CMB are so low that I don't think there's any way to harness the energy - even in a science fiction type concept like this!
the rays NASA's lunar shield idea wanted to deal with we're solar
flare/fission generated, however the same principle of attraction/repulsion
should (?) apply to CMB (which happens to infiltrate space like loose snow on a
mountain side or a very very heavy blizzard), the lunar shield idea was to
repel flare/ray radiation, what im wondering is if it would be possible to use
a similar but differently arranged "shield" setup to work like the caterpillar
tracks of a snowmobile "on" the CMB [abridged]
Submitted sanguine.digitalis"AT"googlemail.com 2/10
The CMB is extremely isotropic. Hence there's no special direction that you could use to pull momentum out of the background. So this isn't at all like surfing the solar wind, which you could certainly imagine doing in principle.
How is the blackbody spectrum connected with the cosmic microwave
background radiation?
Submitted by sreerajt90"AT"gmail.com 10/10
The CMB has spectrum is extremely well fit with a blackbody shape. In fact it may be the best blackbody that we have ever measured!
I understand the concept of CMBR as being evidence of a hot Big Bang, and I am
trying to preempt some questions that I am sure some of my more astute freshmen
will ask. My understanding of CMBR is that as the universe expand(ed), it
cooled, which implies that it originally had more heat (energy). Is it
plausible to assume that the very early universe was mostly gamma radiation that
cooled to become microwave radiation as it lost energy (or as wavelengths
lengthened to fill the expanding space of the universe)? If this is so, is it
then plausible to assume that as the universe continues to expand, the microwave
radiation will eventually lose enough energy (or the universe will expand enough
that the wavelengths will lengthen even further) to become radio waves?
Submitted by amy.pugel"AT"sbcglobal.net 10/10
Yes, the CMB was once a "Cosmic Gamma-ray Background" and will one day become a very long wavelength "Cosmic Radio Background".
You seem to have a pretty good grasp of what is going on, and probably don't need me to answer your questions!
Does the Cosmic Microwave Background travel through space or is it always
everywhere? If it travels, has it passed Earth already?
Submitted by ryanburnscanada"AT"yahoo.ca 12/10
The CMB photons travel through space at the speed of light and are everywhere! They don't originate from a specific place, but from all of the early Universe, so the photons are coming to us from every direction. And that will continue to be the case in the future, as we see back to greater distances.
When asking the question: "Where did the Big Bang take place?", the answer
would be: "Here!" since it happened everywhere (in a yet non-expanded Universe
13.7E9 years ago).
Now, our instruments (FIRAS, WMAP, etc.), which detect the CMB photons, are
also located "Here"!
The CMB photons have been traveling 13.7E9 (-300.000, in this context
considered insignificant) years only to end up the very same spot
("Here"), from where they were also emitted.
Please describe the trajectory, the CMB photons have followed during this
journey. They have travelled along straight lines, but how do they then manage
ending up the same place, they started? Does this observation support the idea
of a "Closed Universe"?
Submitted by carstenegedal@gmail.com `01/11
The CMB photons which we detect here and now were not emitted here in the past, but rather come from some different part of the Universe in the past. Specifically, they come from a distance away which is the light travel distance in the age of the Universe (which is like the distance in light years, except a bit bigger because of the expansion).
I suspect that the confusion comes from a mental picture in which the early Universe was small - this is wrong! You should try to picture the Universe as being very big even at the earliest times.
Regarding the fact that photons are now reaching us from all angles after
having travelled from some other place for 13 billion years, this implies that
we are at least 13 billion light-years away from any 'edge' of the universe (by
edge I mean the edge of how far the unverse has expanded and therefore from
where any photons could be departing). - Is this true?
Submitted by lenn@shaw.ca 01/11
We can only really learn about the part of the whole Universe which is contained within our "observable patch". So you're right that other, more distant parts of the Universe could be quite different, and there would be no empirical way of finding that out. I think the idea of an "edge" is pretty unlikely (and in fact if you do really dramatic things just outside our patch, then you'd expect at least a gradient across our patch, which might be observable) - but certainly there's nothing to stop conditions being quite different if you go extremely far from us.
In the answer to your next to last FAQ you state "So the photons that we
observe in the cosmic microwave background were created in the first minute or
so of the history of the Universe. Subsequently they cooled along with the
expansion of the Universe, and eventually they can be observed today with a
temperature of about 2.73 Kelvin."
Doesn't Thompson scattering prevent radiation from escaping the plasma?
Other references state
that the origin of CMBR "is some 400,000 years later when radiation and matter
became decoupled (time of last scattering)." Which is correct?
Submitted by a.rousseau1"AT"comcast.net 03/11
This is partly philosophy or semantics!
The "last scattering surface" is at a time around 400,000 years, and is the time earlier than which there is lots of Thomson scattering. But this process does not create photons, it just scatters them. (Although if you want to split hairs, then you could regard the process as the absorption of a photon and emission of a different photon in another direction).
At earlier times the scattering can change the energy of photons, but still doesn't create them. To find a process which genuinely makes new photons, you need to go back much earlier, to times of about 1 year. But unless there are unexpected things happening at this epoch (like the decay of some unfamiliar particle) then photons will be both made and created in equal numbers - and so the net creation of photons is still close to zero. The last process which definitely made new photons was when the electron-positron pairs (which were once in equilibrium with the photons) annihilated as the Universe cooled. That was at around a minute after the Big Bang.
Hello Mr Scott, I am trying to understand CMB and why, when the photons that
it comprises were generated soon after the big bang, we can still detect
them. Two questions arise that none of the web articles even mention:
1. Why hasn't this radiation been absorbed by matter?
2. If light travels in a straight line, why isn't all this radiation
now a long way beyond the space that is occupied by matter?
Submitted by sjgrant"AT"btinternet.com 03/11
The answer to the first question is that the Universe is pretty empty on average! The photons of the CMB interact very little with anything until they come to the Earth's atmosphere, or the detector!
Although you say that you can't find answers to your second question - in fact this is one of the most widely asked questions, and there are lots of answers to similar questions on this page. The basic issue is that your mental image of the Big Bang is probably wrong - it isn't a small localized patch of radiation travelling out in all directions, but a whole Universe full of radiation travelling in all directions from all positions at this early time.
The photons observed in the cosmic microwave background have cooled
along with the expansion of the Universe, and observed today with a
temperature of about 2.73 Kelvin.
If expansion of space continues, will the temperature basically ever
reach .00000000 Kelvin and since matter stops moving at that temperature,
will space stop expanding?
Submitted by cattleya1h"AT"sbcglobal.net 03/11
This is a good question!
You're right that the CMB temperature will continue to fall as the Universe expands. As far as we know, with vacuum energy dominating today's cosmos, the expansion will continue forever. However, if you wait long enough, then the typical wavelength of photons will be similar to the size of the whole observable Universe. At that point the concept of "temperature" doesn't really mean anything any more. So that would be the ultimate temperature - but it's very very small!
Is our galaxy moving away from the big bang at the speed of light?
I always thought not. We can see galaxies moving faster than us and so we
can't be travelling as fast as the speed of light.
Is there some sort of refraction or reflection?
If not, to me, this means that we are not seeing the CMB for the creation of
our galaxies, as the light from this would be well past our area of the
universe? How long did the big bang go on for?
Submitted by oz_hotz"AT"yahoo.co.uk 04/11
The "Big Bang" was not a place, but a time everywhere. If you can get that concept sorted out in your head, then you'll be a long way towards answering your questions yourself!
The other main idea which is key here is that the "Hubble expansion" (i.e. more distant galaxies are moving away from us faster) is precisely what you get in a medium which is uniformly expanding. All observers see other parts of the Universe moving away from them.
The CMB that we observe (in all directions) is moving away from us at essentially the speed of light, and marks the locations of photons that left the early Universe and have travelled over about 13 billion years to reach us here and now.
I understand that our area
of the universe was once a peice of the big bang that has expanded out and
cooled into our space.
But it still doesn't make full sense to me. The universe has expanded very
slowly, compared to the speed of light. The size of the universe in the
early expansion was small enough that the faster light would quickly cross
the entire universe and come out the other side, leaving it only present at
the edge of the universe? I understand that time has expanded as well, but I
can't see how this would slow the light down.
And a normal photon that is produced, in say an explosion will travel
through space, not time. Why are the photons that were created at the birth
of the universe able to travel not through space (we are the same point of
space that they were created, just later in time. Other photons do not
travel in time?
Submitted by oz_hotz"AT"yahoo.co.uk 04/11
I'm afraid that it sounds like you still have the wrong picture in your mind.
There are several answers on this page which go into this at length. But let me give you the short version here, focussing on statements you make which are not correct.
You say "the universe has expanded slowly, compared to the speed of light" - that's not true! If you consider somewhere far enough away from us, it is expanding faster than the speed of light - that's how uniform expansion works. You say "the size of the universe in the early expansion was small enough that ..." - this is also not true! The early Universe should be considered as a space of infinite extent, all of it expanding. You mention "the edge of the universe" - but there's no such thing! You say that you don't understand "how this would slow the light down" - but it doesn't! Light always travels at the speed of light! Lastly, you say that "we are the same point of space that they were created" - but that's not the case either! The photons which were created here are long gone. We're seeing the photons which were created many billions of light years away.
I should be grateful if you would explain why the CMB was not discovered
earlier.
Submitted by tony.laverick"AT"ntlworld.com 04/11
That's a very good question!
The answer is a long and complicated one, involving several twists and turns - which with the benefit of hindsight may appear to be missed opportunities. But I suspect that many science discoveries have equally complicated histories!
I won't give you my own version of this story - because I'm really not an expert on the details (not being old enough to have been there!). You can find some useful information on the internet (e.g. the "Discovery of cosmic microwave background radiation" on wikipedia). More first-hand information can be found in the book "Finding the Big Bang", edited by Peebles, Page and Partridge (published by C.U.P. in 2009).
Is Cosmic background radiation, radiation of photons and microwaves?
Submitted by rahmaniz68"AT"gmail.com 05/11
Yes!
Electromagnetic radiation can be thought of as either waves or particles. Low energy particles correspond to long wavelengths (much longer than the visible light that you can see). The radiation from the early Universe peaks in the microwave part of the electromagnetic spectrum.
Next week I'll have to do a presentation on CMB. Your site did answer
excellent questions, but I'd like to know a short and easy way to describe
CMB.
Submitted by luvyduvylaura"AT"gmail.com 05/11
I suggest you look at the top-level explanation on this site, which is here.
Good luck with your presentation. If your audience have questions, and you've read all of this page beforehand, then you should be able to answer all of them!
I cannot understand why we can detect any CMB. My reasoning is as follows:
Submitted by tchancellor"AT"comcast.net 06/11
This question, in various forms, has been answered several times on this page! The short answer is that your mental picture of the early Universe is probably not correct and is misleading you into a paradox. The early Universe is big and photons are emitted in all directions. The CMB that we see consists of those photons which happen to be reaching us now. So they were all emitted from a sphere around us, of a particular radius. Different observers are seeing photons coming from different parts of the early Universe.
What is the average, not peak, wavelength of the CMB?
Submitted by umassie"AT"comcast.net 07/11
I think this may be a genuinely new question, thanks!
The answer depends on precisely what you mean (just like asking about the peak of the CMB). Perhaps the most reasonable answer would be to ask more precisely for the average frequency of a photon. This is a particular integral over the CMB spectrum, weighting the frequencies with the function for the distribution in number of photons over frequency. I think (let me know if you spot an error here) this is 153.4 GHz. If instead you were to ask for wavelength, then it would be reasonable to use the weighting of number of photons per unit wavelength, and this would give an average of around 3.606 mm. The average wavelength is not exactly the same as the wavelength you get by converting the average frequency, for just the same reason that the usual value given for peak wavelength doesn't correspond to the value for peak frequency (since the relevant functions per unit wavelength or per unit frequwncy are different).
I was fascinated to see that c.3% of TV static was causes by the CMB.
I was wondering if you could tell me how it manifests itself as TV static?
I.e. how does the TV static relate to the CMB - would a fluctuation in temp
result in a variation in the static produced?
If you were able to filter out the 3% or so static caused by CMB what would it
look like on a TV? [abridged]
Submitted by www.pstevensonkeating.co.uk 08/11
The idea is simply that one of the major sources of "noise" is thermal fluctuations. Since room temperature is about 300 Kelvin, and the CMB is about 3 Kelvin (and exists everywhere), then somewhere around 1% of noise in a simple room temperature detector will be from the CMB. Of course real detectors will be more complicated in practice. Other sources of noise might dominate a particular kind of detector, making the CMB contribution much smaller. On the other hand, modern TVs (for exmaple) have all sorts of digital filtering going on, reducing noise, and they typically don't even allow you to tune between channels!
So how much of the "snow" on a TV screen is due to the CMB isn't an easy question to answer in detail. In any case, this is "pure noise", in the sense that you're not going to see anisotropies on your TV screen. So if you had images of the Universe giving you secret messages (like in the movie Poletergeist perhaps), then you're out of luck!
I am trying to clean up a Wikipedia page and want to use your
web page as a source reference. I am trying to determine the
level of the cosmic background radiation in order to add a supporting
reference to this Wikipedia page:
http://en.wikipedia.org/wiki/Orders_of_magnitude_%28power%29
which has this entry that needs a reference:
"3 uW astro: cosmic microwave background radiation
per square meter"
Your Frequently Asked Questions here:
has the following line for the flux:
"This gives approximately 3.14 x 10-6 W/m2."
But I tried to doublecheck your number, and I had a hard time finding
any other online source. The closest I was able to come was a UCLA page:
http://www.astro.ucla.edu/~wright/CIBR/
has the following line
"The CMB is by far the largest of these radiation fields, with a total
intensity of 996 nW/m2/sr."
When I multiply 996nW/m2/sr by 4*pi steradians I get 12.5 microwatts per square
meter.
This is 4 times larger than your 3.14 microwatts per square meter.
Am I wrong to multiply
by 4*pi?
Submitted by Not Ed
The issue is that there's an ambiguity of a factor of 4 depending on precisely what quantity you are talking about.
If you have an isotropic radiation field (or actually any isotropic distribution of particle velocities) and you ask about the flux of particles crosses unit area (imagining holding a 1 m^2 sheet out in front of you), then you get a factor of 1/4. In other words: Flux = (1/4) c * (energy density). The factor of 1/4 comes from averaging over angles relative to the plane surface. This is a standard result in what is usually called "kinetic theory" or statistical physics.
A consequence of this is that when you work out the flux for a blackbody, you get: Flux = sigma T^4, where "sigma" is called the Stefan-Boltzmann constant, and contains within it a factor of (1/4) compared to the "radiation constant", which connects energy density with temperature.
To estimate the CMB flux, I simply used this Stefan-Boltzmann equation, with sigma=5.67 × 10-8 (in SI units). With the usual value for the CMB value of T you get something like 3.13 × 10-6W.m2.
Is it possible to determine the direction of the source of the CMB?
Submitted by ifabiovarella"AT"hotmail.com 03/11
Yes!
The CMB is coming from all directions. So the source is "everywhere". The entire early Universe was hot, and emitting photons. We see the parts of the Universe that are the light travel distance away.
Can we Say "Detection of Microwaves in Space" as an Evidence to support
Expanding Universe, other than the normal Redshift phenomenon.
Submitted by avinashatsjce"AT"gmail.com 03/11
Not directly. We simply know that there is "blackbody" radiation everywhere, and if we also know that the Universe is expanding, then that means that the radiation was hotter at earlier times. So it's supporting evidence for the "Big Bang" picture, and the part which makes it the "hot Big Bang".
However, it's also possible to look at the physical conditions in distant gas clouds, from which the temperature at high redshifts can be estimated. Hence we have some information about how the CMB temperature changes with time. And that is independent evidence for expansion.
Do em waves behave like sound waves? Is there peak and trough reinforcement
when when 2 waves collide?
Do protons have a frequency? What was the frequenCy of the big bang?
Submitted by itsatz"AT"gmail.com 01/13
Electromagnetic waves behave like sound waves in the sense that they are both wave phenomena. However, there are also fundamental differences between them. It is quite common for people to use analogies with sound waves in order to understand electromagnetic waves. But you should be aware that these are only analogies, and if you push them too far they will break!
So, yes, EM waves can interfere, just like sound waves. And there's a well-defined wavelength and speed.
The CMB is composed of radiation with a range of wavelengths (and frequencies), all travelling at the speed of light. So there was no specific "frequency of the big bang".
I recently bought a book on cosmology, and it says a lot of stuff about
CMB.I just wanna know what CMB is and what part does photons play in this
.The book said that the radiation cooled from 3000k to 2.73k over the course
of 13.7 billions years.What radiation is this and can ypu please tell me
what are photons, I know what they are but I need an explanation for it.
Submitted by ryuhayabusa35"AT"gmail.com 02/13
The CMB is photons! Photons are particles of electromagnetic radiation, or in other words, light. The ones in the CMB were made in the early Universe as high energy photons, and have been cooling as the Universe expanded - so that we observe them as microwave radiation today.
Enjoy your cosmology book!
In your Q&A,
you explain well that intergalactic dust and collapse of microscopic black
holes, for instance, would not explain the properties of CMB spectrum.
As a chemist I would not suspect molecular or atomic gases either, as then
we would see absorption and emission lines. However, how do we know that the
current-day intergalactic proton-electron plasma, having no chemical
structure and thus no spectral lines, is not the reason for CMBR? Is the
intergalactic gas dense enough to produce microwave radiation, or any
radiation at all?
Submitted by tuomas.kangasniemi"AT"hotmail.com 03/13
The intergalactic medium is full of gas, mostly hydrogen, but with very low average density. Still, there's no way for it to produce a "blackbody" spectrum, because it's not "optically thick". Plasma can emit other sorts of radiation, as well as absorbing in hydrogen lines. We see all of that, so we have direct evidence of what's out there in the space between galaxies. But there's no way it can make the CMB.
In one of your answers, you told the speed and direction of Sun
w.r.t. the CMB rest frame. I find this topic extremely intriguing. However,
although I know some geometry, I am not familiar with astronomical
notations. Thus could you give the direction of motion in ecliptic latitude
(north pole in north) and in longitude w.r.t northern spring equinox (the
direction of Earth's orbit being the positive angle)?
Submitted by tuomas.kangasniemi"AT"hotmail.com 03/13
I'm not sure what coordinate system you would prefer. It sounds like you are asking for ecliptic coordinates. It's easy to find tools on the internet for converting between coordinate systems - so you should be able to figure this out in whatever system you like.
Ecliptic coordinates don't really make sense for things beyond the Solar System though.
Why we can detect CBS? Shouldn't CBS photons
which were created 300 000 years after big bang overtake us billions years
ago? Space wasn't so big than. One explanation would be that we detect
reflected CBS radiation? But obviously astronomers made young space CBS map
so that it cant be true.
Submitted by hektor70000"AT"gmail.com 07/13
I'm assuming that you are referring to the CMB here.
What you are asking is probably the most asked question about the cosmic microwave background. And it is answered several different ways on this page! The key to the answer is that the statement "Space wasn't so big" is not correct.
When we look a star, we say the light took so long to travel to us. So
tomorrow we will see star that is one day (our time) older than before.
Is this true for the CMBR as well? As each day passes, do we loose a day
(our time) of information?
Submitted by erodrig_97"AT"yahoo.com 07/13
You're right that when we see the CMB, we are seeing back effectively one more light day every day.
But it's not true that we're "losing information". We're actually in some ways seeing more information as time goes on, because we're seeing back to a bigger chunk of the Universe. This is related to the question that people regularly ask about "why have the CMB photons not already passed us?" The point is that we're seeing a slightly different region of the early Universe as time (for us) goes by.
If you're really interested in the details of the information content contained in the CMB, and how it will change over very long time periods, then you should have a look at this paper I wrote with two colleagues! You can get the pdf version here (or an earlier shorter paper here).
Is the universe very small at the period of CMB?
If so, photons from CMB with speed of 300 000 km/s run into what?
Light outrun the expansion of the universe because the universe is
expanded only at the rate of 74,2 km/s per megaparsec(3 millions
years). When lights hit the boundary if there is one, what happened ?. Did
it bounced back?. Or it continued straight into something not known?
Submitted by trai_nc"AT"hotmail.com 11/13
No! The Universe was not small when the CMB was released from the matter. Although the Universe has been expanding, you shouldn't think of it as being "smaller" in the past, but rather than everything was closer together. In other words it was denser, but it has always been very very big.
So there's no boundary, and no edge to the CMB photons. Every day we see photons coming to us from further and further away. And there's no evidence that there's an end in sight.
Thank you for your answer but i am still very confused. Since the CMB was
released from the the very dense and hot matter, that matter universe should
be then much smaller especially that universe is created from the big
bang, a single point. With times, the matter was stretched by the expansion
of space and the matter universe become bigger and bigger.
Is that possible that the CMB are also from very far away stars(some 12,13
billions of light year) from all directions?. If so, there is no ends for
the CMB and the CMB is no proof for the big bang.
Submitted by trai_nc"AT"hotmail.com 12/13
I'm afraid some of the starting assumptions are still not correct - and that's the basis of your confusion. You say "universe should be then much smaller especially that universe is created from the big bang, a single point". However, you shouldn't think of the very earliest phase of the Universe being a point (localized in space), but already a very large volume that was originally very hot and dense. We see the heat coming from all around us because the early Universe was hot everywhere.
Is CMB moving or is it stationary?
Submitted by gabklein"AT"gmail.com 02/14
The CMB photons are moving at the speed of light, in all directions. There's a reference frame defined by these photons, in which the sky looks isotropic. If you measure a "dipole" (i.e. one side of the sky brighter than the other) then you know you are moving relative to this "CMB rest frame".
I am a ninth grade student ... and I will be
giving a group speech on how cosmic microwave background proves the Big Bang
theory. I need to use props to explain this and I wondered if you had
suggestions. I also need to involve the audience in my speech. Any help you
can give me would be greatly appreciated.
Submitted by themiller5"AT"comcast.net 04/14
This is a great question, and I'm struggling to think of a helpful answer! Explaining the CMB to a general audience can be quite challenging. So props would definitely be good, as would involving the audience somehow. But I'm not at all sure what to suggest. Maybe someone else reading this has some ideas?
What was the wavelength of the photons generated at the time of big bang and
how their wavelength reached microwave?
Submitted by "Muhammad Idris"
When the photons were first generated they were very high energy gamma-rays. They had a range of wavelengths, characteristic of a "blackbody" spectrum at a very high temperature. As the Universe expanded the wavelengths stretched and we observe the background peaking in the microwave part of the electromagnetic spectrum today.
Is it possible then to compare the size of
the universe with what it was at the time of big bang based upon the ratios of
photon wavelengths then and now?
Submitted by "Muhammad Idris"
You can compare the "scale factor", i.e. the function which sets how much everything has expanded. The ratio of temperatures (or peak frequencies of the radiation) at 2 different epochs is the reciprocal of the ratio of scale factors. But this doesn't tell you about the "size of the Universe". The whole of the Universe is potentially infinite in size, with no edge, no centre, etc.
What I don't understand is why we should still be seeing this
radiation at all. It should have left at the speed of light.
Expansion of the universe notwithstanding, shouldn't it have passed
us up by now?
Submitted by nick.stama"AT"gmail.com 06/14
"Why has the CMB not passed us already" is the single most asked question about the CMB! This demonstrates that you are thinking about what's going on, but still don't quite have the right picture.
Please read other answers that are on this page!
Could the cmb be the blast wave of the Big Bang and the expansion of the
universe be
the galaxy's far away enough to be pushed by the force of the explosion but not
close enough to be destroyed by the explosion.
Submitted by aperition_1"AT"hotmail.com 10/15
This seems like another variant on the "Why has the CMB not passed us already" question.
The "Big Bang" was not an explosion! An explosion happens at a specific place, but the rapidly expanding Universe was a process occurring everywhere at once!
However, the CMB is the cooled radiation left over from the early Universe, and so in a sense is related to what you are asking.
Big Bang was one point. Why CMB is coming from all over then?
Submitted by dan.serbanescu"AT"me.com 10/14
This is yet another variant on the "Why has the CMB not passed us already" question.
The "Big Bang" was not one point! Who told you that?!
With the expansion of the universe CMBR is becoming "stretched" to longer
wavelengths therefore it began as a shorter wavelength. Why when we look at
distant places in the universe don't we see these longer wavelengths, why is
it all microwave, shouldn't we expect to see infra red or visible as we are
effectively looking into the past?
Submitted by pwynne"AT"loretogrammar.co.uk 10/14
When we "see" light we're actually detecting the photons that arrive where we are. So the CMB photons are being seen as they are now, not as they were when they last interacted with matter in the Universe. They were roughly visible wavelength photons when released from ionized material in the early Universe, and as they travelled towards us in the expanding Universe their wavelengths stretched so that they peak at microwave wavelengths today. We're seeing the photons that arrive here
In simply but
factual layman terms what is CMB? Where did it Come from? What does its
near uniformity suggests? What does its anisotropy mean?
Submitted by pd.delwaar"AT"gmail.com 12/14
It's the "cosmic Microwave Background", which, as it says, is a background of cosmic microwaves!
It's the cooled radiation that fills the Universe, and used to be hot. It comes from everywhere. It's near-uniformity tells us that something (and many of us think this was something like the idea called "inflation") made different bits of the Universe the same at early times. The small amplitude anisotopies tell us about how variations in density have been evolving as a function of scale - and that gives extremely tight constraints on precisely what sort of Universe we live in.
In space, we only see the Sun when we look directly at it. When we look away
from the Sun we do not see it nor
any of its light. Yet we see the CMB in all directions. That seems impossible
given that it is widely concurred that
the universe is flat. It would only seem possible to see reflections of the big
bang radiation reflecting from gases and dust in space.
If the CMB is the radiation of the big bang, then it would seem that this
radiation began from a relatively small object. Thus my analogy to our Sun.
Submitted by alanadler24"AT"att.net 02/15
The Sun is an object in a particular direction, but the "Big Bang" is a time in the history of everywhere in the Universe, and hence you can't point to it. Or more accurately, you can point to it, but in any direction.
As described in the answers to multiple questions on this page, the mistake that many people make is to picture the early Universe as a small region within a much larger space. Since this is the whole Universe we're talking about here, it was never a small region within some larger thing. The "Big Bang" happened everywhere in a large extended Universe, and hence we see the CMB coming to us from all directions.
This list has several objects at a distance of 13 gly.
Current thinking is that the CMB is 13.8 gly distant.
It challenges credibility that objects 13 gly distant are only seen when you
look directly at them, yet an object 13.8 gly away is seen in all directions.
I'm quite skeptical.
Submitted by alanadler24"AT"att.net 02/15
The CMB is not an object, but a time, or in other words it's the distance that light is reaching us from every direction, the light-travel time ago. (As an added complication it's not 13.8Gyrs ago, but a bit bigger, because the Universe has been expanding as the photons travel towards us - but that's not the main issue here.)
For some people it helps to think of being in a huge crowd at a sports game, with everyone cheering at once, and the region from which you hear people cheering being a circle around you. The CMB is just the same, except it's a sphere rather than a circle.
I was reading your questions and answers about cosmic microwave background
radiation and I have a question about it.
You say that CMBR can be observed today at a temperature of 2.73 kelvin. Would
you happen to know what that is in Celsius (centigrade)? I have searched all
over the internet and I can't find a way to convert kelvin into centigrade. I
thought perhaps you may know.
Submitted by magictheunicorn"AT"outlook.com 06/15
I don't understand why it isn't easy to find this information on the internet, since (for example) google has a built-in facility for converting between units. But in any case, the answer is that you simply subtract 273.15. However, no self-respecting physicist would use Celsius to describe the temperature of the CMB. Zero on the Kelvin scale has a clear physical meaning, and since the CMB temperature is only a few degrees above zero, then it would never be referred to as -270.4245 Celsius (or even -454.7641 Fahrenheit!).
Why are these photons still here? Travelling at light speed,
wouldn't they have passed all matter by now? And why do they appear to
be coming from all directions? Have they already reached the boundaries
of the universe and now on their way back?
Submitted by marktieman"AT"outlook.com 10/15
This is a very good question! In fact, it is so good that it has already been asked and answered many times on this web-page. It is the single most asked question about the CMB, and comes from an incorrect picture in whichthe early Universe is finite in size. Please scan this page for more detailed answers.
Corollary: Does the fact that photons from the big bang are coming
at us from all directions prove that the universe is finite. Can this
be used to estimate the its size?
Submitted by marktieman"AT"outlook.com 10/15
Yes, for the "Observable Universe". But there's almost certainly a lot more to the Universe that we can't see (yet).
I am
trying to find out the angle that the Solar System Eclectic makes with the
CMB.
It states in the attached paper that --"the known dipole direction, (l; b) =
(264_; 48_), of 384 km s^-1 _ 78 km s^-1 (stat:) _ 115 km s^-1 (syst:)"
Sorry to ask such a basic question but I have no background in Astronomy. Is
the 48 effectively the angle above the eclectic plane of the Solar System as
marked onto the image below in red ? If not is it possible to tell me how
much angle I would need to add or subtract to get the actual angle.
Submitted by paul"AT"tdesign.net 01/16
I think you mean "ecliptic" (probably auto-spell-check!). But actually those coordinates you quote are "galactic coordinates", i.e. given with respect to the plane of the Milky Way on the sky, and nothing to do with the Solar System or Earth. You have to rotate into what are usually called "equatorial coordinates", with the "longitude" called "Right Ascension" and the "latitude" called "Declintation". I think you may be asking about the angle that our direction through the CMB makes relative to the Earth's equator, which would be the declination of the CMB dipole, which is about -8 degrees. On the sky the direction of our motion through the CMB is near the boundary between the constellations of Crater and Leo, on the Crater side. If you're really interested in the direction relative to the "ecliptic" (i.e. the main plane of planetary motions in the Solar System) then you can look up the "ecliptic coordinates" for that location on the sky via the internet.
The angle I am looking for is the angle of the plane of the solar system
compared to the direction of the movement of the solar system through the
CMB.
I understand that the solar system moves through the CMB at approximately
370 km/s but I need to know the angle. Although I am not an astronomer, I
would be surprised if that would be described as Ecliptic latitude of the
constellation Crater.
Is this something that you can help with ?
Submitted by paul"AT"tdesign.net 01/16
The plane of the Solar System is the Ecliptic plane. And hence the angle that (I think) you're looking for is the angle relative to that, which is the Ecliptic latitude of the direction we're moving in, and hence approximately the latitude of that small constellation in Ecliptic coordinates. This looks like about -11 degrees.
I have difficulty in understanding CMB and I hope you might be able to put me right.
My issue, considers that the big bang occurred at a single point, a singularity. I
also think that this point ought to still exist within the universe, in some
absolute coordinate system it is the origin. But this gets me into trouble with CMB.
Logically the CMB has been traveling radially outwards at the speed of light since
shortly after the big bang. Whereas the material solar system in which we live must
surely be travelling at sub light speed but still away from the origin. So in my
simple minded approach we should not see the CMB since it has travelled long ago
beyond our location.
Clearly wrong!
So how do we explain the CMB? Is it closer to reality to see the entire universe as
in escence that single point. This would mean that the singularity has become
everything and that the "direction" towards the location of the big bang is all
directions?
Submitted by M.G.Rose"AT"sussex.ac.uk 04/16
This is probably the most asked question about the CMB, and you can find it (in various forms) further up this page!
The basic answer is that it's not helpful to think of the Universe starting at a point, but rather to consider that the early Universe was very large, and CMB photons were emitted from everywhere in all directions.
Can you tell me the speed and direction of the earth's velocity vector
through the CMB?
(Plus a reference would be appreciated!)
Direction in layman's terms would also be appreciated.
Submitted by profsjones@gmail.com 07/16
The velocity vector depends on what frame you want to measure this in. That's because everything is moving, e.g. the Earth is spinning on its axis, and orbiting around the Sun, while the Sun is going around the centre of the Milky Way Galaxy, our Galaxy is moving towards the Andromeda Galaxy, our Local Group is moving towards the Virgo Cluster, etc.
The convention is to quote the velocity in the "heliocentric frame", so that it takes out the Earth's motion, but still contains the velocity vector of the Sun around the Milky Way added to all larger-scale motions. In this case the answer is about 370km/s towards a position in the small constellation of Crater (whose coordinates you can look up if interested).
When the universe cooled to a point where photons could escape
the originally opaque cloud that was the universe (the dawn of
"transparency") what was their original wavelength? Simply put, what form of
radiation has CMB redshifted from? Given that, at our current rate of
expansion, the cosmic background radiation is uniformly in the microwave
spectrum, can we assume that the original wavelength of these photons were
also uniform? If so, what part of the spectrum? Visible? Gamma?
Submitted by John Reese johnl.reese"AT"live.com 04/17
The CMB spectrum is a "blackbody", which means there's a spread of wavelengths, with a well-defined shape, specified only by the temperature (and basic physics). The typical wavelength is inversely proportional to the temperature, so that today we have microwave photons for the roughly 3K temperature.
The Universe went from being mostly a plasma to being mostly neutral at an early time that corresponds to an expansion factor of approximately 1100. This means that the Universe at that time was about 1000 times hotter and the typical photon had a wavelength about 1000 times shorter than today's. That makes them basically optical photons.
However, these weren't the "original" photons, because they still existed at earlier times, while the Universe was opaque. If you go to early enough times the photons were gamma rays.
Will there ever exist a point in time where our rate of expansion
from the center of the universe will have become so fast that we will have
surpassed the cosmic background radiation? From my knowledge, any CMB seen
today must have been emitted with a hubble sphere of the original
singularity that was the universe. Anything emitted beyond that volume
centered on the initial point of the big bang would become un-observable.
Submitted by John Reese johnl.reese"AT"live.com 04/17
Note that we're not expanding from the centre of the Universe. There is no centre of the Universe! We're just part of the whole expanding Cosmos, everything expanding away from everything else.
Please, please, please, if you've ever read that the early Universe was finite in size, just forget that entirely and start again with a picture in which the early Universe was already very big! With CMB photons effectively being emitted from everywhere at some arbitrarily early time. If you have the correct picture, then there's no need to ask your question, because we're always seeing more CMB photons that were emitted from further away.
Why can't the thermal equilibrium of the CMB be explained by
assuming that the matter produced before 10 to the -43 seconds of the big
bang was already in thermal equilibrium?
Submitted by drlarryvescera"AT"gmail.com 07/17
I think this is essentially the standard picture! A hot dense early state is naturally in thermal equilibrium. You don't have to assume anything, since if it wasn't in equilibrium (e.g. because you added a whole bunch of particles at one particular energy), then it would quickly reach equilibrium through various scattering processes being "fast" (relative to the rate at which the Universe is expanding and cooling). That's why the thermal spectrum of the CMB is such string evidence that the early Universe was hot and dense.
I still do not understand
the source of the assumed disequilibrium following the Big Bang? Is the
assumption that the Bang was in disequilibrium and expanded faster then the
speed of light so the disequilibrium of the Bang was preserved in the CMB?
Submitted by drlarryvescera"AT"gmail.com 07/17
There's no assumed disequilibrium! The point is that it doesn't matter what happened at super-duper early times, since any out-of-equilibrium state will very quickly relax to a thermal equailbirium. It's just that with everything being so hot and so dense, the rates of the processes for reaching thermal equilibrium are short compared with the expansion rate. That's why the CMB spectrum is so well fit by the blackbody spectral shape.
Sorry to be so dense but you seem to be indicating that the thermal
equilibrium of the Universe is accounted for. It is my understanding that
it is not: because the universe is expanding faster then the speed of light
therefore the thermal disequilibrium coming out of the initial quantum
fluctuation from which the Big Bang originated is not explained. What am I
not understanding correctly?
Submitted by drlarryvescera"AT"gmail.com 07/17
Every piece of the early Universe was in thermal equilibrium. The fact that some parts of the Universe may be expanding at arbitrarily large speeds from others parts isn't really relevant here.
There's a somewhat related phenomenon, wt might be getting confused here. What I'm referring to is the "horizon problem", where it's not clear why one side of the CMB sky should be the same temperature as the other side, since they're only just now coming into causal contact. This is explained in the inflationary picture in which a small causally connected (i.e. size less than the age of the Universe times the speed of light) patch at early times expanded exponentially (with parts exapnding from each other faster than the speed of light). But this doesn't really have anything to do with thermal equilbrium - which is a good approximation everywhere at early times.
So the photons that were created in the early universe had a much smaller
wavelength than observed in the CMBR as being microwaves. The explanation
for this that I am seeing is that the universe cooled so the photons lost
energy and got larger wavelengths as they cooled.
Is this explanation correct? The problem I have with it is that it makes
sense that a bunch of high energy photons that get spread out should bring
the universe to a lower temperature because they are spread out now so the
energy density is lower. So although we observe photons in the microwave
region I don't see why this should be because the universe is cooler and not
some other phenomenon. Because it seems like the cooling of the universe can
be explained by having same wavelength photons but spreading them out so the
energy density is smaller.
Submitted by koitf1"AT"investigatetachyons.com 07/17
The photons have longer wavelength because the Universe has been expanding. And longer wavelength photons mean exactly the same thing as a cooler temperature. So there's no other phenomenon.
The universe, under present cosmology doesn't have a centre or an edge, or a
preferred direction. It is therefore not possible to be in motion with respect to
the universe.
Submitted by achu4112"AT"uni.sydney.edu.au 12/17
This isn't true.
The photons are moving, at the speed of light, in all directions. However, there's a frame in which the photon distribution is statistically isotropic, i.e. pretty much the same in every direction. If you're moving relative to that frame you'll see a CMB "dipole", i.e. one side of the sky will be brighter (or hotter) and the opposite direction will be fainter (or colder). That's because it's the effect you get for a uniform sky when you boost to a different frame of reference.
Hence you can tell your speed relative to this special rest frame.
The photons from the cosmic background radiation were emitted ~13.4 billion
years ago, 380,000 years after the big bang. They have been in route for
all that time. How did we get here before they did in order to detect them?
The universe was ~380,000 years old when the photon was emitted and started
its journey. Our space and the energy that would become us was part of
that 380,000 light year universe. If the universe expanded slower than the
speed of light the photon should have passed us a long time ago. If the
universe was expanding faster than the speed of light the photon would
never have caught up with us.
Something is wrong.
Submitted by rolds105"AT"gmail.com 1/18
What's wrong is that you're implicitly assuming that the CMB photons were released from a region of small size inside a much larger universe. In fact the CMB photons originate from everywhere in a very big cosmos!
This is essentially another version of the most common question asked about the CMB. There are already many answers (above this one on the web-page) answering this in several different ways.
Your answer "CMB photons originate from everywhere in a very big cosmos"
still does not answer my question. I read all the Q&A's and I'm still not
getting it.
After inflation the universe was the size of a basketball. I read that
there is no outside of the basketball, there is nothing, no time, no space,
no energy, nothing.
There is no outside of the basketball. (I wonder if the quantum foam exists
outside the expanding bubble)
300,000 years later the universe was still pretty small only ~600,000 light
years in diameter. [abridged]
Submitted by rolds105"AT"gmail.com 1/18
Problems can arise when people oversimplify things in an attempt to put forward an explanation that sounds good for their immediate purpose - but without following through the consequences.
I think that's partly what is going on here. Somewhere you read that after inflation the Universe was the size of some everyday object (it might be a basketball or a grapefruit, or whatever). But this is just a way of trying to help you visualise that the region contained in today's observable Universe used to be very much smaller.
No one thinks that the cricket-ball was everything there is, and that it is embedded in "nothing". It's simply the size of the thing that expands to be the Hubble scale today.
You should try to erase any notion you have of "smallness" for the early Universe. In reality the whole of the Universe was very much larger than the illustrative water-melon. So much larger, that you may as well regard it as infinite in the first place.
Now you just picture that all the places in that first instant were giving off radiation, and today we're just seeing the part that's the light travel distance away from us.
Hard to get my mind around this. Your saying "Regard the whole of the
Universe as infinite
but the big bang only banged out the " region contained in today's
observable
Universe". This still doesn't answer my original question of where that
CMB photon
as been for 13 billion years since the "observable universe" was much
smaller when
it began its journey. I guess I'll just have to chalk it up as another
paradox that
I'll never get my mind around.
I read that the "ants on an expanding balloon" idea is how we should think
of it
1) every ant thinks he is the center of the universe, 2) all the ants
observe the other ants are moving
away from each other. 3) there is no edge. Since the surface of the
balloon is
a 2D surface with the 3rd dimension hidden from the ants, applying that
idea
to a 3D universe would require a 4th hidden spacial dimension.
Submitted by rolds105"AT"gmail.com 1/18
So let me try this one more time. I really don't think it's hard to understand! It's just that you've already got some notion in mind that you have to replace with the correct picture.
It's not that "the big bang only banged out the region contained in today's observable Universe". The bang banged everywhere! We only see CMB light coming from the light travel distance around us. And in your ant analogy, every ant sees light coming from a sphere around them, i.e. every observer has their own observable patch of the universe.
There's a nice analogy with hearing the sound of the crowd from a circle around you, imagining yourself in a giant crowd at a sports event, when everyone sees the goal at the same time. This is described in more detail in some answers above (search for the word "sports") on this page.
What can be concluded from the CMB about the time dependence of fundamental
constants?
For example, in the enclosed paper
"An upper limit to the cosmological variation of Planck's constant derived
from the spectrum of the microwave background radiation"
it is claimed, that there is no time variation of Planck's constant.
But at the end of the paper the author seems to admit that he is mostly
measuring h(antenna).
Submitted by Lampe.Bodo"AT"web.de 5/18
That's a good question, and one that may not have yet been answered on this page!
With a little thought you can appreciate that quantities with dimensions cannot be measured to vary. This is basically because you'd get a different answer depending on how you define units. This means that only the variation of dimensionless quantities can be considered. So I'm afraid that the particular 1977 paper you refer to is fundamentally flawed.
Nevertheless, there are reasonable constraints that one can place on combinations of physical quantities that are dimensionless. The most popular example is the "fine structure constant", which describes the strength of the electromagnetic force in a dimensionless way. Another example is the ratio of the electron mass to the propton mass. Constraints on these parameters from CMB observations are discussed in several papers, e.g. the one called "Planck intermediate results. XXIV. Constraints on variations in fundamental constants", published in 2015 (on which I was a co-author).
I read that peak frequency of the Microwave Background Radiation is 160.23 GHz.
160.23 GHz / (2^30) = 149.225816 Hz.
That's closest to a D note in music. Did I calculate that right?
D3: 146.83 Hz
Now I'm wondering, what are the next two or three peak frequencies, the secondary peak frequencies? I thought it would be fun to calculate those pitches and see what chord might be vibrating out there. Are the frequencies are slowly changing over the eons due to the Doppler Redshift as the Universe expands? Or are they are not changing as much as our perception of them?
Submitted by john"AT"klemport.net 5/18
Interesting question!
First of all, I think your number for the peak frequency of the CMB spectrum is more or less correct (I think I'd give the number to be 160.4GHz), and hence it does seem like it's equivalent to about a D, shifted by many octaves.
However, one thing to realise is that the CMB spectrum is very broad, and so is very different from what you'd hear as a pure tone.
The next thing to say is that I'm afraid you're confusing the frequency spectrum with the "power spectrum of anisotropies". It's this second thing that is often compared to music, since the physics is acoustics, and hence there's a "fundamental mode" and a series of harmonics. I realise that it may be easy to confuse these two things: the frequency or wavelength spectrum, often called a "Planck" or "blackbody" spectrum; and this "power spectrum" of modes on the sky that's related to acoustic oscillations. However, they're really very different things.
For a discussion of the relationship between the CMB power spectrum and acoustics, see for example the material prepared for public lectures on "big bang acoustics" by Mark Whittle: here.
I recently read a paper in the monthly notices of the royal astronomical
ociety saying that the CMBR was from intergalactic dust and not from the Big
ang. It(the paper) also claims that it(CMB) could not be from the Big Bang
ecause it could not survive the 13.7 billion year history of the universe and
ould have been altered by the opaque epochs of the universe. I am writing to
ou for your take on the paper.
The Paper:https://doi.org/10.1093/mnras/sty974
Submitted by subomiadeyemi7"AT"gmail.com 6/19
This is an old idea, which appears to have been revived. There are plenty of reasons why this makes no sense. To be honest, I'm surprised this was published in "MNRAS", since it is very easy to poke holes in this claim.
For one thing, it's nearly impossible to make such a good blackbody spectrum without it coming from a time when the whole Universe was in thermal equilibrium. Dust grains just don't make that good an approximation to a thermal spectrum, however you try to arrange things.
Then there's the business of the Universe getting more and more opaque, so that the optical depth reaches unity at some redshift that's lower than where we routinely detect galaxies. There would surely be dramatic effects on the brightness of objects at high redshift, which we don't see.
On top of all that, there's are the CMB anisotropies. These fit a simple Big-Bang type model, with only half a dozen free parameters. It's inconceivable that we're on the wrong track here. And certainly there's no reason to take seriously an alternative idea that doesn't even begin to predict the CMB anisotropy power spectrum.
i go high school. I would like to work on Project that is related to CMB.
Could you give me ideas what experiment I can do? With simple Equipment?.
Submitted by rodas1rosy"AT"gmail.com 8/19
This is a good question. But it's not easy to give a good answer! It depends on how experienced you already are, how much effort you're willing to put in, how much help you're likely to get from others, etc.
It's certainly possible to build your own experiment to measure the CMB. It's also possible to build something to make a map of the sky at microwave wavelengths, where you can tell that there's the Milky Way across the sky (which for CMB purposes we try to remove of course). But I think it's very unlikely that you'd be able to build for yourself something that detects the anisotropies or measure the frequency spectrum, since those things are genuinely difficult to do. Remember that such precise measurements were only achieved in the 1990s with large numbers of professional scientists with lost of money and equipment! Reproducing instead the simpler things that were first done many decades ago is going to be much easier.
What I'm saying is that it's possible to build your own radio telescope, and this is effectively the first step towards building your own CMB detection experiment. Radio wavelengths are the low frequency end of the CMB, and the technology is much more straightforward to deal with than at the higher frequencies where the CMB peaks. Penzias and Wilson first detected the CMB at 4GHz, which is far from the peak frequency.
So my advice would be why not try to make your own radio (as opposed to "microwave") telescope and see how far you can get? There are lots of resources available online. For example, there's an organisation called the Society of Amateur Radio Astronomers, who have suggestions. But I'm sure you'll be able to find descriptions by other high-school students who have successfully done this in the past.
what is the rate of change of the image, how long does it take to create the
mage, and the next time it is created what time difference does the new data
epresent, how often has an image of the background radiation been generated,
or example if the image is 13.8 billion years old has an image been taken
f 13.7 billion years old
Submitted by jimmy.pantelleria"AT"gmail.com 4/20
This is a good question, and in fact I've written a couple of papers discussing detailed answers!
But the basic answer is very simple - the CMB sky just doesn't change on a human timescale. The map that's made today is just the same as the map that was made yesterday - although a map made in just a day would be fairly noisy. You have to integrate over a decent length of time to beat the noise down, ut the images of the sky made by the Planck satellite each year are tatistically the same (varying only because of the minor effects of instrumental noise). And the images taken earlier by the WMAP satellite are also the same (at least at low resolution, where the data sets overlap).
The CMB sky does evolve, but only on cosmological timescales. You'd have to wait a really long time to see any differences. It would be an interesting thing to do, since in principle it gives us more information about the Universe. But unfortunately none of us will be able to gather enough information from the changing CMB sky to be useful.
I found the below question and answer on your CMB email questions page.
[regarding the peak frequency of the CMB spectrum]
I have three questions of my own concerning it.
1. Would the scientific D (Pythagorean) be closer to the note that the
reader is looking for (D=144).
2. What are the other three main CMB frequencies and what would be their
closet music note following this method
Submitted by firesurfer7"AT"gmail.com 9/20
The important thing to realise is that the CMB frequency spectrum covers essentially all frequencies! It's not a specific "harmonic", like a musical note. There's a well-defined peak, but even there, the precise value of the peak depends on whether you're referring to the intensity per unit frequency interval, or per unit wavelength interval, or some other definition.
Because of the wide spectrum, if you converted the CMB waves into sound waves, you'd hear a whole mess of notes together. So it would be more like a "noise" than a musical tone.
I've read the excellent Q&As on your website, however I still don't know
ow to get information from the CMB picture, Yeah, the commonly seen picture.
ould you please help me to have a comprehensive view of this picture?
Submitted by yuntong1994"AT"126.com 12/20
This is a good question. How does someone, who doesn't already have a background in university-level physics and statistics, understand how information is extracted from maps of the CMB? I'm struggling to think of something published that's at the right level. I can think of many popular books that offer a simplistic overview, and many cosmology papers that go into the technical details. But there's just not very much in between!
Maybe this means there's a niche there for someone to write something!
All I can think of to suggest for now is that you read more of my Q&A
pages, particularly regarding anisotropies, and then whatever details you don't
follow, you can try google. Then you can build up to understanding the
technical papers. For example my review article, which you can find
here.
CMB - Anisotropy
How do I get an intuitive
understanding of the origin of the acoustic peaks?
through the
phase when the
fluctuation bounces back to minimum temperature, the temperature looks like
a rarefaction? Shouldn't it just bounce back to its original size and
(over) density?Submitted anonymously by a senior colleague!
(These peaks in the "power spectrum" of CMB anisotropies are caused by the effect of large-scale sound waves around the time the photons were last scattered.)
I think that's a good question! The answer lies in the fact that the whole heuristic explanation is a bit confused about whether it's in real space or Fourier space. Plus it avoids any mention of gauge choice (ie exactly what you do above the horizon size) etc. So to some extent the basic picture doesn't stand up too well to such questioning! All that aside, I think it is possible to answer your question simply. You should think of this overdense blob as getting a kick from gravity when it comes inside the horizon (ie becomes causal) - thus it is a driven acoustic oscillation. So you would expect the "starting point" to be the equilibrium then the radiation falls into the potential well, ie it goes to maximum compression, then bounces back (due to the baryon pressure) to overshoot the equilibrium and become a rarefaction. I hope this helps!
I have been reading tons of
technical papers and the idea of an "angular power spectrum" keeps popping
up. It's hard to bridge the gap in this field between the extremely
low-level information and the extremely technical. What is this entity?
Submitted by jlh22"AT"dana.ucc.nau.edu
Different experiments are sensitive to different angular scales. Think of a CMB experiment as measuring a set of temperature of the sky in "pixels" of some angular size (set by the smallest scale which can be resolved by the particular telescope) over some region of the sky. The size of the pixel and the size of the region of sky are the smallest and largest angular scale that are probed. The information obtained from a CMB experiment is then the variation in the temperatures at some particular angular scale, or perhaps a range of different angular scales.
For the COBE satellite, for example, these variations in temperature were measured over a range of angular scales from about 7o up to the full sky. Other experiments tend to have higher angular resolution and also cover just a small fraction of the sky. When we put together a whole bunch of measurements at different angular scales we end up with an estimate of how the temperature variations change as we change the angular scale. A plot of this, ie "temperature variation" versus angular scale, is referred to as an "angular power spectrum" -- it's the amount of "power" in the temperature fluctuations plotted as a function of angle.
In fact you want to be more mathematically precise than this, and instead of "angular scale", you really want to deal with the amplitudes of a set of functions which are independent of each other and which probe different angular scales. Such functions for the sphere are called "spherical harmonics", and have well-understood properties. The spherical harmonic which describes variation over the whole sky is called the "monopole", while variations of 180o are described by the "dipole", variations on scales of 90o are described by the "quadrupole" and so on. The index of the harmonic is the "multipole" number, so that a small multipole number corresponds to large angle, and a large multipole number corresponds to a small angle. What is actually plotted then is the square of the amplitudes of these spherical harmonics versus the multipole number. This is the "angular power spectrum", and it can be interpretted as meaning the variation in temperatures as a function of angular scale (size of "pixel"), plotted so that large angles are on the left and small angles on the right.
I am having difficulty understanding how the odd acoustic peaks in the
power spectrum can correspond to fluctuation compressions, while the even
peaks correspond to rarefactions. It seems to me that
we should see equal power in compression and rarefaction.
Submitted by desai"AT"orca.astro.washington.edu 2/99
Ah, a technical question! The details of how the microwave background fluctuations vary with angular scale can be somewhat esoteric - however, the basics are pretty straightforward: the density perturbations were oscillating, and we catch them "frozen" at the last scattering epoch. The big bump in the spectrum corresponds to the scale that was first feeling the causal effects of gravity at that time, while smaller scales had already been oscillating for a while. Both compressions and rarefactions lead to enhancements in the temperature fluctuations at those particular angular scales, and so the "power spectrum of anisotropies" ends up as a series of bumps and wiggles.
The specific question (posed by desai) concerns the peaks that come from the compressions versus those that come from the rarefactions. The reason they're not exactly equal is that there's an effect from the regular matter (baryons) which essentially shifts the zero point. This is fairly well explained in the excellent summary called "The Physics of Microwave Background Anisotropies", by Hu, Sugiyama & Silk, which appeared in Nature in 1997, and can be found as a postscript file here. If this seems too complex, you might like to start with the article by Scott & White, called "Echoes of Gravity", which is here.
Why is the background microwave radiation found to be so smooth
since surely a lumpy distribution is necessary to explain the
very uneven distribution of matter in the universe?
Submitted by degs"AT"iafrica.com 10/99
This is a good question, and one which many people were asking prior to the detection of the CMB anisotropies in 1992. Up until then there had only been upper limits to the lumpiness of the CMB sky. The point was that it was difficult to construct models in which the COBE satellite would see complete smoothness, and that would be consistent with the idea that the structure we observe in today's Universe grew through the steady action of gravity. Many people suggested that if COBE gave further upper limits, then we would need to consider much more complicated ideas for how structure formed.
In fact the amount of variation observed in the microwave sky is almost exactly what was predicted based on the most popular models (where the Universe is dominated by some form of so-called Cold Dark Matter). So the CMB sky is just as lumpy as it should be (about 1 part in 100,000) to lead to all the lumpiness we see today, with the simple attractive force of gravity being all that is required to increase that lumpiness over the last 10 or so billion years.
Do the tiny CMB anisotropies constrain the mean mass density of the
Universe in any way, and if it does, why?
Submitted by ib6146"AT"bristol.ac.uk 11/99
The anisotropies in the CMB can be measured as a function of angular scale. Schematically, what you do is make a map of the CMB sky with a certain resolution of pixels, and estimate the variance of the temperature in that map - then smooth the map to a bigger pixel size and repeat. You end up with a bunch of numbers that tell you how "lumpy" the microwave sky is at various angular sizes (technically what is measured is called the "power spectrum", which is really just a better defined version of this same procedure).
It turns out that theories for the formation and evolution of structure in the Universe give quite detailed predictions for this "power spectrum". In particular, the simplest models (compatible with a theory called "inflation", which generated the fluctuations in the very early Universe) predict stronger anisotropies around a scale of about 1 degree on the sky. This seems to be pretty much what the most recent expermental results have been showing.
In a little more detail, the robust prediction of the models is for a characteristic length scale on the sky (corresponding roughly to the distance light can have travelled in the age of the Universe at the time when the CMB last scattered off matter). This length scale will look like a different angular scale on the sky depending on the "curvature" of the Universe. Since the curvature is governed by the mass-energy density content of the Universe, then the precise angular scale of maximum CMB variations on the sky depends on the density of the Universe.
The best available data suggest that these simple theories seem to be a good fit, and that the Universe must be rather close to being "flat" (ie not very curved at all). Since the matter that we can account for comprises only about one third of what is required to make the Universe flat, then there seems to be evidence from the CMB for some additional form of energy that helps keep the Universe flat. This is variously called the "cosmological constant", "qunitessence" or "dark energy". But just because it has several names, it doesn't mean we really understand what it is!
Could you give me the angle formed between the rotation axis of Earth
and the axis of the anisotropy dipole of CMB.
Submitted by mcrotti"AT"inlab.com.ar
As you no doubt know (if you've read any of the rest of this page at least!), there is a so-called "dipole" pattern on the CMB sky. In other words one half of the sky is a little hotter than average and one side a little colder. This is a Doppler effect, casused by our motion through the Universe.
Precisely what direction you give for this dipole depends on what other velocities you have subtracted off first. For example, we know that the Sun is moving around our Galaxy, so do you want the dipole in the rest frame of the Sun or the rest frame of the Galaxy? For the Solar System, the answer is that the motion is towards celestial coordinates RA (longitude) = 11.20 hours (or 168o), Dec (latitude) = -7.2o. Since this coordinate system has the "celestial equator" defined as the projection of the Earth's equator on the sky, then our motion is -7.2o from the equator. So the answer to your question is that the Solar System is moving through the Cosmos at an angle of approximately 83o from the Earth's South Pole.
In fact the annual variation in the Dipole, casued by the Earth's motion around the Sun, can also be seen by an all-sky experiment that lasts more than a year. This is a direct measurement of the Earth's motion, and in a sense proves that the Earth is going round the Sun rather than the Sun going round the Earth (not that this has been doubted for a few hundred years!). The COBE satellite detected this annual variation so well that it could be used to calibrate the instrument - since we know precisely how fast the Earth is going round the Sun (30 km/s), then we know precisely how big a variation should be measured.
What are the standard model CMBR anisotropies and how do they come about?
Submitted by mbliss"AT"oberon.ark.com 2/00
The CMB anisotropies come about from a combination of effects due to interaction of photons with perturbations in the density of the Universe on a range of scales. Various aspects of this question are discussed in answer to other questions on this page.
There is really no "standard model" as such. The general paradigm that seems to fit best is that the initial perturbations were of the sort produced during an inflationary period in the very early Universe (which isn't necessairly to say that inflation happened!). These evolved from being initially of roughly the same amplitude at each scale, to the situation we observe today where they vary with scale in a complex way. This variation encodes the values of a number of fundamental parameters which describe our Universe: the average density in each of the important components, including each form of dark matter; the expansion rate; the amplitude and scale-dependence of the initial density perturbations; the contribution from gravity waves; and some recent processing of the anisotropies by scattering in the reionized Universe, gravitational lensing and other effects.
The promise of the new CMB experiments is that we will ultimately know the values of these parameters. Assuming that this "standard paradigm" (inflationsry-insipred cold dark matter dominated Universes) continues to look good, then the experiments will nail down the parameters and provide us with a detailed "standard model". The alternative is that the general picture fails to fit everything, implying either that there is some crucial missing ingredient, or some whole new paradigm is required. The new CMB experiments should tell us that also.
After comparing several sources, I have noticed that there are different
numbers where isotropy is concerned...is it 1/1000, 1/10,000, or 1/100,000?
Submitted by JULIE108"AT"aol.com 4/00
It depends exactly what you mean by isotropy.
The CMB sky is totally smooth down to one part in 1000. At that level you notice that one side of the sky is hotter than the other side of the sky. This is the "dipole" caused by our motion through the Universe. So you can say that the sky is isotropic to 1 part in 1000.
When you subtract off this motion effect you find the remaining temperature map of the sky is incredibly smooth. You don't see any features in this map until you get down to the 1 part in 100,000 level. The sky has an overall temperature near 3 Kelvin, while these anisotropies are differences in temperature which are typically tens of micro-Kelvins. So apart from the motion effect, the CMB sky is isotropic at the level of about 1 part in 100,000.
Assumption #1: There are no preferred inertial frames, leads to general
relativity... but the CMB provides a preferred inertial frame. If the CMB
obeys the laws of physics, and it shows the way to a preferred inertial frame,
then physics as a whole is not the same in all frames, in contradiction to
Assumption #1.
Submitted by smithe"AT"mrcwdc.com 4/00
Although I've answered similar questions before, I know that this concept is still troubling to some people. So let me make a couple of additional remarks here. Firstly, the description of an expanding Universe involves general relativity, and not special relativity. So it's not necessarily the case that you should expect the ideas of special relativity (which are, let's face it, less general!) to apply. Special relativity doesn't really deal with non-inertial frames. So, for example, you can in principle (described consistently within general relativity) discover observationally that the Universe is rotating, even although (within the context of special relativity) your inclination might be to ask "rotating with respect to what?".
But more importantly you have to examine the assumptions more closely. Let us go back to Einstein. A translation of his original 1905 statement is: The same laws of electrodynamics and optics are valid for all frames of reference for which the equations of mechanics hold good. We will raise this conjecture (the purport of which will hereafter be called the `Principle of Relativity') to the status of a postulate...
There is indeed a frame of reference (actually it's expanding, but never mind that!) in which the CMB dipole would be measured to be zero. But there is nothing special about the laws of physics in that frame. Photons behave as you expect, the laws of electromagnetism are no different, and F=ma is still true.
I dont understand why the variance of energy distribution isnt
calculated which depends on the square of planck's spectral fn and Bose
statistics. Is this due to plasma formation prior to photon gas
formation?
I'm afraid I don't understand this question.
The CMB is composed of photons, which follow the so-called Planck function (the blackbofy shape to the spectrum), and are governed by the so-called Bose statistics (since photons are bosons). However, the fluctuations in photon number caused by those Bose statistics have no cosmologically observable effects that I can think of.
How are the parameters calculated and verified from the observations?
Submitted by ian.watson0"AT"tinyonline.co.uk 6/00
This is another great question. However, I'm afraid that a full answer would be very long, and also rather technical! This in fact is what I spend a bunch of my time doing research on, so I could very easily bore you here!
The short answer is that the fundamental observable is the CMB anisotropy "power spectrum", which tells you how the variations in temperature depend on angular scale. This power spectrum can be calculated for simple models of the origin and evolution of the fluctuations - which grow into our present-day structure and leave their imprint on the CMB sky. These predictions give a power spectrum which contains a series of what are often referred to as "bumps and wiggles"! The details of these features depend on the precise values of the cosmological parameters which describe our Universe (densities in each of the species of matter, expansion rate, a couple of parameters to describe the initial state of the fluctuations, some recent astrophysical processing effects, etc.).
When you have a decent CMB anisotropy data-set you can try to fit the power spectrum estimate, and then constrain the various parameters to the ranges where the models fit the data. At the moment the flatness of the Universe (essentially the sum of all the densities in components of matter and energy) is well constrained, and there are some limits on other parameters too. But we're still in the situation where the answer depends to a large extent on how wide a range of models you're prepared to consider. Things will continue to get better as the bumps and wiggles are pinned down more accurately. It is realistic to expect that in the near future the CMB (in combination with other cosmological measurements) will allow quite precise determination of most of the important parameters simultaneously.
There have been many relevant articles at a range of levels, in various magazines and journals. In the UK, you could check out back issues of New Scientist for example. If you can view postscript files, then the most introductory article I wrote is called Echoes of Gravity, and although a few years old it may still be useful. And for a more recent discussion of measurements of the curvature of space you could look at another article I wrote, Still Flat After All These Years!.
I would like to ask an
explanation about CMBR peak. The first Doppler peak as approximately 200
divided by the 
.
Actually where it comes from?
Is there any effects of
on this peak?
Submitted by hsrashid"AT"pcu.helsinki.fi 5/00
This is a question about the angular position of the peak in the CMB anisotropy power spectrum. In other words, what is the characteristic angle on the CMB sky?
The answer is that there is a characteristic length built into the
known physics of the sound waves which are important for the evolution of
small-scale CMB anisotropies. This length scale (essentially the distance
a sound wave can travel in the age of the Universe at the last scattering
epoch) doesn't depend very much on the model. But the angular scale that
it appears on the sky depends on the curvature of space. The main dependence
is on whether space is flat or not, which is determined by the total
mass-energy density parameter tot.
In a Universe with flat geometry the characteristic angular scale is just
below 1 degree on the sky (or a peak at about multipole 200 in the power
spectrum). In a Universe with closed geometry the angle is
larger, and in a Universe with open geometry the angle is smaller. The
dependence is approximately proportional to
. The fact that the peak in
the power spectrum appears to be near multipole 200 (corresponding to an
angular scale just below a degree) is taken as very strong evidence that
the Universe has close to flat geometry. Since the total density parameter
in all forms of matter that we know of amount to perhaps
mat=0.3 to 0.4, then this tells us that
some other form of energy (which does not cluster like matter) makes up the
deficit. And so there is good reason to believe that
=0.6 to 0.7.
This is either a "cosmological constant" (energy density of the vacuum)
or something even stranger!
In detail the position of the peak also depends on other parameters, such
as , but these
vairiations are quite weak.
For a more detailed discussion, which is still (hopefully!) quite readable,
let me refer you (again) to the article
Still Flat After All These Years!, which I
wrote with two of my colleagues.
ok where can i find pictures of backrounds???
Submitted by Lildevil200114"AT"aol.com 5/00
The best images of the CMB sky are probably still those obtained with the COBE satellite. COBE mapped the whole sky, but with an angular resolution of about 7 degrees. So the COBE maps show a projection of the entire sky (typically into a particular oval shape that would have the plane of the Milky Way as a horizontal line through the middle) at any of 3 frequencies (or combinations of all 3), with a fairly accurate representation of the largest-scale features. They can be found at the COBE DMR images page.
The COBE maps only contain information on the biggest angular scales, since the large beam of the COBE telescope effectively smoothed the maps. But more recent experiments have mapped parts of the sky at much better angular resolution. A good example is the map from the antarctic flight of the BOOMERANG experiment, which can be found in various forms on the BOOMERANG Press Page.
I have one really big question....
I'm a student of engineering in first year so i'm not an expert in
physics or something...
Ok the question is... How CMB proves uinverse is flat?
Submitted by soponcho"AT"geocities.com 5/00
I've answered similar questions above. So let me be brief here. For more details you could read, for example, the article Still Flat After All These Years!.
The basic point is that there is a characteristic scale set by the physics
of the evolving density variations in the early Universe. This characteristic
length scale will appear to be a different angular scale on the sky
depending on the overall curvature of space (which you can think of as making
parallel lines diverge or converge in open and closed spaces, respectively).
Recent measurements of the CMB sky indicate that this scale is just about
where you'd expect it to be in the most popular models, provided
that the geometry of space is approximately flat. It could, of course,
still be a bit open or a bit closed, but it has to be quite close to flat.
More explicitly, the total value of the density parameter
= 1.0 ± 0.1 approximately.
Is "anisotropy" pronounced annieSOTTrippy or anneyeSOTTrippy ?
Submitted by george.barnes"AT"tafe.nsw.edu.au 6/00
It's the latter.
We invented this word deliberately as a sort of secret hand-shake -- if you can pronounce it properly, then you're allowed into meetings of the Clandestine Members Bureau.
(Follow-up comment):
why not include a small embedded media file of the correct pronunciation of
anisotropy?
why not tell people to look
it up on Merriam-Webster's site, which includes nifty
little sound
samples to help everyone get their tongues around it. What I can't
get the hang of is not the emphasis placement, but NOT saying a long
"o" for both "o's".
Submitted by frank.j.glazer"AT"verizon.com 3/03
Good idea! Although I suspect that not everyone will be able to play whatever format the file is in. Any volunteers to send me a short audio file that might be widely playable?
Now that you can pronounce it you will be allowed into the Clique for Mellifluent Badinage!
(Another Follow-up comment):
I just went to your FAQ page, looking to find out how to pronounce Anisotropy.
While I appreciate your efforts, the answer you posted was no help at all!! I
was hoping for a phonetic spelling, with syllable breaks and an accent mark!
Oh well, I'll keep looking...
P.S. Note that I do not know how to pronounce anisotropic either, so your
explanation that knowing how to pronounce this adds confusion to pronouncing
anisotropy just makes it more confusing! With explanations like this, I hope
you don't make a living teaching! Thanks for taking the time to post the FAQ
page, and please take these comments as the good hearted ribbing that it was
intended to be.
Submitted by jigger"AT"Mafi-Trench.com 10/04
Ah, thanks for those words of praise! As you say, it is indeed lucky that I don't try to make a living from teaching!
As to providing a phonetic pronunciation guide, complete with upside-down letters and obscure alien accents, I'm afraid I don't know how to produce them in a way which is readable on different sorts of computers and browsers and which is comprehensible to the average cosmologist who didn't take a linguistics course!
I have a book beside my desk called a "dictionary", which specialises in this sort of thing, and indeed has a pronunciation entry for both "anisotropy" and "anisotropic". If you really want a phonetic transcription, you might try there.
But I made an attempt at copying this - here's the jpeg, and pdf versions.
Your explanation of the correspondence between CMB hotspots and last
scattering surface overdensities was intriguing. Is the overdensity the
cause of positive delta T but gravitational redshift ? Can these two cancel
out?
Submitted by george.barnes"AT"tafe.nsw.edu.au 6/00
This may get a little technical, so let me take a deep breath and give this a go!
The gravitational redshift results in a decrease in the temperature for a postive enhancement in the density. The effect of the density, on the other hand, depends on what type of fluctuation we have. In the most popular sort (called "adiabatic", where the source that made these perturbations didn't change the entropy, and is what you most easily get out of inflationary models, as well as appearing to fit the current data pretty well), the density effect gives more temperature where you have more matter. So the two effects partly cancel. On the other hand there's a different kind of perturbation you can set up in the early Universe (called "isocurvature", where the overall energy density is unperturbed), in which the radiation is overdense when the density enhancement is negative. In this case (which is much less popular, since it doesn't fit the data at all well) the two effects have the same (negative) sign.
Either way, you tend to have a negative temperature fluctuation when the overdensity is positive. In principle the two effects could exactly cancel out, but that would require that the kinds of matter and energy which dominate the Universe would have to be very different from how we think the Universe behaved at the time the CMB photons last scattered and got these temperature variations imprinted.
Why is it exactly that we study the polarization of the Anisotropy? What
is it that we intend to learn from this?
Submitted by noam"AT"asiaa.sinica.edu.tw 7/00
This is a very good question.
There are several parts to the answer. Firstly, the CMB is predicted to be slightly polarized through the scattering process by which it last interacted with matter. No one doubts that the polarization is there, and so it's detection will be a confirmation of the basic paradigm for the physics of the generation of CMB anisotropies. And if there is no polarization, that would be much more exciting of course!
Once the polarized CMB sky begins to be mapped in detail, then there is information which can be extracted from these signals which complements what can be determined from the temperature anisotropies. In particular the polarization is a much cleaner "snapshot" of the "last scattering surface", and so encodes more direct information about conditions back a few hundred thousand years after the Big Bang. And also the existence of very large scale gravity waves (which might be left over from certain kins of processes which happened in the very early Universe) leaves a distinct imprint on the CMB polarization. If this imprint could be detected then we would learn important information about the origin of the seed perturbations which gave rise to all the structure in the Universe.
The CMB sky is predicted to be polarized at about the level of one part in a million, so it will be challenging to map the polarization in detail. But the pay-off is sufficiently exciting that several experiments are underway to do just that.
I'm interested in knowing what the actual measurement differences were in
obtainin the background radiation values.
Submitted by KBeran2140"AT"aol.com 9/00
I assume what is meant here is the size of the temperature differences measured in CMB maps. All CMB anisotropy measurements are essentially differential, i.e. experiments measure the difference between two temperatures. Since differences are measured then what is being studied are the variations in temperature relative to the average value of about 2.725 Kelvin. These variations need to be measured with an accuracy of about 10µK (or at least the average of a whole bunch of measurements of the same thing has to be this small) before you have much of a hope of detecting the anisotropies. The hottest feature seen in a CMB map has a temperature of about 100µK or 0.0001 Kelvin. And the coldest feature has a temperature of about -100µK (relative to the background temperature).
Where can I find out more about cosmic variance, sample variance
and window functions? Can you point me to any helpful papers?
Submitted by TelfordRE"AT"Cardiff.ac.uk 10/00
A technical question!
For readers of this page who are wondering what the question means, let me first explain the terminology. "Cosmic variance" refers to the idea that when we measure properties of the CMB sky we might be able to do so with arbitrary precision, but the information we can extract about the properties of the cosmological model cannot be obtained with arbitrary accuracy. The reason is that our particular sky is one realisation of a statistical process described by the model (the model predicts the variance of the temperatures as a function of angular scale, not tha actual pattern of temperatures).
The fact that individual experiments only have a finite amount of information about the sky is usually referred to as "sample variance". This is just the same thing as asking any statistical question with limited information. For example asking what fraction of the time a coin comes up heads when you have only tossed it a finite number of times - this will always result in a particular level of uncertainty which depends on the number of coin tosses. For the CMB, the "sample variance" is smallest when an experiment has mapped the whole sky, and then the "sample variance" is the "cosmic variance". And you can't do better than this, because there's only one sky to observe!
A "window function" is the name given to the function which tells you the range of angular scales that a particular experiment is sensitive to. This depends on the amount of sky covered, the beam-size (angular resolution) of the telescope, and the particular scanning strategy adopted.
I'm not aware of anything terribly informative on these topics which is not written at a technical level. For details on "sample variance", you could start with a paper by myself and a couple of my collaborators (Scott, Srednicki & White, 1994, Astrophysical Journal, volume 421, pages L5-L8), which you can get here. A good paper on window functions is this one by White & Srednicki (1995, Astrophysical Journal, volume 443, pages 6-10), which you can get here, and another, by Knox (1999, Physical Review, D60, 103516), is here.
I would like to know what the fluctuations in the CMB tell us.
Submitted by hurstds"AT"muohio.edu 11/00
Many, many things!
At a basic level, the fluctuations tell us that the density variations on large scales in the early Universe were about 1 part in 100,000. This turns out to be about the right amplitude for gravitational instability (i.e. the fact that overdense regions become more and more overdense with time) to have formed all the structure that we observe today over the history of the Universe. So the simple observation of these fluctuations confirms that gravity was the force that grew all of the structures (galaxies, clusters of galaxies, etc.).
By measuring how the fluctuations vary with angle, we hope to be able to determine a large number of the fundamental parameters which define precisely what sort of universe we live in. Already it appears that the CMB fluctuations tell us that the curvature of the Universe is very close to flat. And additionally that the sorts of very early density variations which the Universe possessed appear to be like those obtained in so-called inflationary models of the early Universe. We fully expect to learn vastly more in the coming years!
Could you point me to some resources that may contain
information on the calculus behind CMB.
Submitted by pufffy13"AT"yahoo.com 12/00
The mathematics behind the general concepts involving the CMB is in fact quite straightforward. It's when you come to try to understand the anisotropies in the CMB that things get more challenging! I suggest that you start by going to your local bookstore or library and looking for any books they have on cosmology which are at some intermediate level between the popular text and the full-blown research textbook. Only you will be able to tell if it's the right next level for you!
Eventually you might be able to work up to the full mathematical treatment of the anisotropies. One of the most elegant and complete discourses is a paper entitled "A Complete Treatment of CMB Anisotropies in a FRW Universe" by Hu, Seljak, White and Zaldarriaga, which you can get as a postscript file here.
On the right side scale of to-day's picture there are negative
temperatures in microkelvin. I thought that, by definition, the minimum
temperature in kelvins was 0. What is your definition of the kelvin
temperature scale?
Submitted by lermanma"AT"csolve.net 12/00
The picture you are referring to is a map of part of the CMB sky made by the MAXIMA experiment, which was featured on the Astronomy Picture of the Day site for 30th December 2000.
The temperature scale for that map is for temperature anisotropies rather than absolute temperatures. In other words what is measured is the temperature difference relative to the average temperature of the CMB sky. The CMB temperature is a little less than 3 Kelvin, while the temperature differences shown on the map range between about -0.0003 Kelvin and +0.0003 Kelvin (or 300µK, i.e. 10,000 times smaller). In fact the experiment only measures temperature differences, and isn't sensitive to the overall average value (which requires a different sort of experiment to measure). It would be possible to add back in the roughly 3 Kelvin "DC level" for the map, but then the anisotropies would be such low contrast that you wouldn't be able to see them.
The 2.7K CMB seems to consist of standing waves to me.
I would greatly appreciate your comment on this aspect of the
2.7K CMB. [abridged]
Submitted by henry"AT"govital.net 1/01
Let me first define a "standing wave", for others who may read this answer. Think of a standing wave as a pattern (on a string, say) with a fixed wavelength but with amplitude getting bigger and then smaller with time. There are points on the pattern (the nodes) which don't move at all), while between the nodes the displacement is biggest. There it goes through maximum, back to zero, then negative, back to zero etc. There's a nice animation here. This is what waves on the strings of a musical instrument behave like. The wave pattern itself doesn't travel along the string, and this distinguishes standing waves from "travelling waves". In travelling waves the pattern of the wave moves along at some particular speed (like waves on the surface of water for example).
The CMB does not consist of standing waves, but of travelling electromagentic waves, i.e. photons. These waves move at the speed of light, and were emitted in all directions by every part of the very early Universe.
However, standing waves do play a role in the physics of the CMB. The bumps and wiggles in the power spectrum of CMB anisotropies can be thought of as standing sound waves. By precisely measuring the anisotropies over a wide range of scales we can determine the amplitudes of all these sound wave harmonics, which tells us about the fluctuations in the early Universe, and how they evolved. This in turn tells us about fundamental properties of the Universe that we live in.
In the maps of CMB can you see two different size blobs corresponding to
the first and seconds peaks of the power spectra?
How do they make the power spectra from the map?
birdjo"AT"Spole.gov 3/01
If you stare hard at a good CMB map (or a simulated one!), you can tell that there's a characteristic angular scale. This corresponds to the scale represented by the main peak in the power spectrum. Probably it's hard to tell by eye that there's a second peak, since there's power over a wide range of angular scales. But for a sufficiently low noise map you should be able to discern that there's a characteristic size for the blobs and that there's structure on smaller scales too. For an experiment with a small enough beam-size, you would notice a lack of structure in the maps on the smallest scales, but still large enough that they're not just smoothed out by the beam - this would be the fact that the power spectrum itself has no power at the smallest scales.
Now to answer your second, more technical question, which is a good one. The crudest way to make power spectra is just to Fourier transform the map. You can bet that that's about the first thing that's done once the maps have been produced! But you need to be much more careful when producing a final estimate of the power spectrum. For a start you need to use spherical harmonics rather than Fourier modes, since the sky is curved, not flat. Then the finite size of the map introduces correlations between the modes. So you need to make binned estimates over various ranges of k, and estimate each of these in a way which is independent of the other values. A fair amount of theoretical work has been done figuring out how to do this efficiently while not losing any information content. The final estimates of power spectra from experiments like BOOMERANG and Maxima take days to run on a supercomputer!
I need to find some good colour images of the CMB for us to use as the
basis for an animation. There are 3 main images I'm after - to show the
differences between open, flat & closed Universe (ie. small, medium &
large 'blotches' of colour).
www.pioneertv.com 6/01
As a start you could look at a picture I made (with Martin White) for the US Decadal Survey in Astronomy, which you can find as a postscript file here. Basically you want a picture of coloured blobs, with stronger contrasts at smaller scales for the open model and the opposite for closed models. So in fact if you're just trying to show artistically what happens, you want to do something which looks like blowing up the small-scale features while keeping the large-scale features the same.
There's also a picture on the Boomerang web-site which is very nice for showing the connection between the CMB and the geometry of the Universe. Unfortunately it doesn't keep the same "phases" for the 3 maps, i.e. each one is a separate random simulation. So it doesn't show the effect as well as it could. But I think you get the idea that open Universes would have much more small-scale features than closed models.
what are some irregularities and what techniques are being used to
detect irregularities in CBR?
Submitted by mo_poon"AT"yahoo.co.uk 10/01
The "irregularities" in the CMB are technically referred to as "anisotropies". They are deviations from smoothness discernible when a map of the microwave sky is made. These deviations occur over a wide range of angular scales. So whether you make a map of a large fraction of the sky with big pixels, or a map of a small chunk of sky with smaller pixels, you will still see variations in brightness. In fact the way that these anisotropies vary with angular scale carries the precious information about our Universe which researchers are now trying to unravel.
To make such measurements you need to be sensitive to brightness differences corresponding to only a few microKelvin, or about 100,000th of the brightness of the CMB as a whole (which corresponds to about 2.7 Kelvin). This can only be done with specially designed experiments to make ultra-sensitive maps of parts of the sky at microwave frequencies. Right now there are a range of such experiments, operating from the roofs of Physics departments, from high mountain observatories, from balloon-borne platforms or from space. Together they promise to build up the full picture of the cosmological information content buried in the CMB sky.
What are the implications for various cosmological models of the
universe?
Submitted by mo_poon"AT"yahoo.co.uk 10/01
Things are really the other way round: we learn about the cosmological model by measuring the anisotropies. The precise variation of the anisotropies with angular scale (how "noisy" the maps look as a function of the size of the pixels) encodes information about the Universe in which we live. We can learn about the initial seeds from which all the structure formed, as well as the amount and composition of dark matter, the rate of expansion, the flatness of space, the overall shape of the Universe etc. That we have the ability to learn all these things by measuring the microwave sky is an incredible opportunity that the Universe has given us.
Since the CMB was emitted prior to star and galactic
formation, why do we not see images in "negative" of
these material structures? I.e., surely the moon
blocks the CMB from a telescope. Surely the sun does
as well. Why not Alpha Centauri? Andromeda?
Submitted by bopbone"AT"yahoo.com 11/01
Absolutely!
The Sun is a local strong emitter of radiation at just about every wavelength. So to make a map of the CMB sky, you have to make sure the Sun isn't in your picture! It's even worse than that though, since you're looking for variations of one part in 100,000. So you have to make sure you don't even see a glancing reflection of the Sun. CMB experiments go to great trouble to reduce any effect of the Sun by observing well away from the Sun's position, as well as having all sorts of shields etc.
The Moon reflects all sorts of light from the Sun, and also glows in the mcrowaves (because the Sun heats it up). So you have to avoid the Moon too.
Even the most nearby stars are still so far away that their effects are negligible. However, that's not true for the whole agglomeration of stars in our Galaxy (the Milky Way). So you have to make CMB maps well away from the Galactc Plane.
Other galaxies will have a smaller effect. This certainly has to be thought about. They block the CMB, it's true, but they also emit radiation on their own. So they will typically be bright spots. There's another effect though that can casuse a "hole" in the CMB at certain wavelengths. That's called the "Sunyaev-Zel'dovich" effect (after the two Soviet scientists who first suggested it might be observable). The idea is that hot gas in the outskirts of galaxies, or in clusters of galaxies can scatter some of the CMB photons. Some of the low energy photons gain energy, and so with a radio telescope you see a hole in the CMB in the direction of a galaxy cluster (and at shorter wavelengths you'd see a hot spot in the same place). This effect has in fact been observed for many of the biggest clusters of galaxies. And presumably as observatioins continue to get better, we'll eventually be able to see this effect for individual galaxies too. It actually turns out to be a useful thing to observe, since it tells you information about the obstructing object that would be hard to tell any other way.
In the CMB rest frame you measure no velocity with respect to the CMB
photons?
I thought that the speed of photons was "c" when measured from any and
all frames of reference. What am I missing?
Submitted by 12/01
It may be that some people (even me, gasp!) have been sloppy with language when explaining the CMB "dipole" effect.
Of course the photons are always moving at the speed of light. So what you detect is not that there's a different speed for the photons in one direction. You simply see more photons (or equivalently a brighter intensity or higher temperature) in the direction you're moving towards, and fewer in the opposite direction. Think of it as a bunch of photons moving about in all directions, and then imagine how many photons will cross a unit area of detector per unit time. If you are in the rest frame with respect to the CMB photons, then you measure the same flux of photons no matter where you point your detector. But if you now move your detector very fast in one direction then you'll get more photons per unit time. It's just like how you get more raindrops in your face when you run in a rainstorm!
So the effect is that if we're moving in some direction relative to the "CMB rest frame", then there will be more photons (per unit area per unit time) apparently coming from that direction, and fewer coming from the opposite side of the sky. That the sense in which we can detect whether we're moving with respect to the CMB photons.
I was recently reading how the COBE has observed very slight variations in
intensity of microwave radiation as a function of direction, but I do not know
what causes this. Could you provide any insight as to the source of these
variations?
Submitted by gte878n"AT"prism.gatech.edu 3/02
Since you can find more detailed answers here on this very web-page, let me just provide you with a brief answer here. They are variations in density observed at the epoch when the photons last interacted with the matter in the Universe, about half a million years after the Big Bang, when the Universe was very much hotter and denser. Sveral other experiments have detected such variations, at a range of angular resolutions, and we're now building up a detailed picture of these minute variations in temperature, which hold valuable information about the structure of the Universe on large scales.
I'd like to know if it would be possible to orient oneself in space by
comparing extremely accurate CMB maps. For example, if one was to make a
hi-res CMB survey map and if one could (by magic!) travel to another part
of the universe hundre ds of millions light years away *instantly*, would
it be possible to determine o ne's location (relative to the origin point)
by taking new CMB measurements and comparing them to the original
measurements? If not, how might such a feat be accomplished?
Submitted by damiensk"AT"pacific.net.au 8/02
This is a very interesting question!
The CMB anisotropies come from the "last scattering surface", which is an imaginary sphere around us, where we can see back to a time when the radiation last interacted with matter. The hot spots and cold spots on the sky come from the overdensities and underdensities on this sphere. Each observer has a different surface, determined simply by the distance that light can have travelled in each direction in about the last 15 billion years. So if we moved, say 1000 light years in some direction, then the CMB map would look pretty much identical. But if we moved some significant fraction of 15 billion light years, then we'd be seeing different density blobs, which would cause different sets of hot spots and cold spots. In fact the "thickness" of the last scattering surface is something like a few hundred thousand light years, and so if you moved further than that, then the features you'd see on the CMB sky would no longer be correlated.
So I suppose if you found yourself instantly in a part of the Universe where the CMB sky looked similar, but a little different from our own, then you could infer that you'd moved by some amount in some direction. It should be possible to quantify that amount, and know where you were. However, if you moved to some part of the Universe millions of light years away, then the maps would have nothing in common (other than the overall level of fluctuations etc.), and so you'd have no idea where you were, other than further than something like a million light years.
How do the COBE results conform with a model with a positive cosmological
constant? Is this model scale invariant too? If not, why do the
physicists bother themselves about it? [abridged]
Submitted by 11/02
The results of the COBE satellite indicated that the initial conditions for the density perturbations (which were laid down in the early Universe and which gave rise to all of today's structure) were "scale invariant". This means equal amounts of fluctuations at all scales. This says nothing about the geometry of the Universe, or about whether or not there is a cosmological constant.
The COBE data are equally well fit with the sort of model which is currently popular, i.e. about 2/3 of the total energy density in a cosmological constant (or "Dark Energy") and the other 1/3 in Dark Matter. However, it's also true that very large amounts of Dark Energy would have left a noticeable effect on the COBE data, which were not seen (so we know the Universe isn't very closed, with more than enough cosmological constant, for example).
In fact the most recent CMB anisotropy data, from several experiments which collected data at smaller angular scales than COBE, also point towards models which contain about 2/3 Dark Energy.
My question concerns
the image generated in the early 90's from the COBE satellite. What was the
significance of this image, apart from confirming the existance of the CMB?
Did the image change our ideas of the background radiation in any way?
Submitted by Andres.Donaldson"AT"stpauls.richmond.sch.uk 11/02
The data from the COBE DMR instrument were the first to demonstrate that the CMB sky contained anisotropies. So the fluctuating pattern in the images showed regions of the early Universe which were a little hotter or cooler than average. The CMB itself had been detected in 1965, but all images made of the CMB had shown it to be extraordinarily smooth (apart from the "dipole' pattern showing our motion through space).
The COBE data measured the amplitude of these temperature variations. And they were pretty much exactly what was needed for the popular "cold dark matter" models to have left those impressions in the early Universe and then grown all of today's structures through gravitational instability by the present day.
So the anisotropies in the COBE data were very important in confirming that the basic cosmological picture was on the right track. That picture is composed of: a hot early Universe, expanding and cooling, containing low contrast density perturbations at early times, which grew over billions of years to produce all of the rich structure of today's Universe. If COBE had detected no anisotropies, or ones with the wrong amplitude or variation with angular scale, then our basic paradigm would have to have been dramatically changed (and there were many cosmologists at the time who were anticipating such a change!).
Newer CMB anisotropy results have further bolstered this picture, as well as filling in some of the details, like the form of the initial density perturbations, the amounts of dark matter and dark energy, etc.
I've read some introductory notes on CMB anisotropy. I saw that most
calculations assume the matter content of the universe as it is, without
considering the fact that the matter content must somehow evolve via
CP-violation processes to produce a net amount of matter.
I wonder if there has been any attempts before to include this
CP-violation processes in CMB anisotropy calculation and if there will be
any observables due to this.
Submitted by haryo"AT"hep.fsu.edu 01/03
It's clear that the vast majority of the Universe is made of matter rather than "anti-matter", and that there has to be a good particle physics explanation for this eventually. At the moment there is no definitive answer to the process which favoured matter over anti-matter, although there are a number of ideas.
The effects which generate this asymmetry occur at very high energies, long before the CMB anisotropies that we see were generated. I'm not aware of any detectable effects of such processes on the CMB anisotropies. But I'd be happy to hear of the details of any idea that you work out!
The uniformity of CBR suggests that the Universe was
very smooth during the first 300000 years. On the
other hand dark matter should have been in clumps that
attracted ordinary matter after the decoupling of
radiation and matter, to form galaxies. But these
clumps of dark matter would affect the geomerty of the
Universe. So the Freedman's smooth viewpoint of the
primeval Universe is wrong and should be replaced by
inhomogeneous models.In this case the CBR ought to
have irregularities. What's wrong with this picture?
Submitted by tomp044"AT"yahoo.co.uk 02/03
This is a very good question!
The answer is something that cosmologists refer to as "gravitational instability". This is the fact that slightly overdense regions increase their contrast relative to the average density (and obviously undersense regions get more underdense) as the Universe gets older. This happens in a regular static medium, and turns out also to happen in an expanding medium (i.e. the Universe as we know it), although at a slower rate. You can think of an overdense region expanding a little slower than a typical part of the Universe and hence increasing its density contrast with time.
The Universe at early times had very low amplitude inhomogeneities. We see these at a time of about 300,000 years through the CMB anisotropies, which have amplitudes of about 1 part in 100,000. These amplitudes have grown by the present time (say 14 billion years later) to form galaxies and the rest of the structure in today's Universe.
What is anisotropy?
Submitted by mriccobo"AT"ucsd.edu 03/03
The dictionary definition is something like "the state of having different properties in different directions". In CMB studies (as in some other fields, like geophysics, crystallography, etc.) this word is used to refer to the quantification of the degree to which something is not isotropic. Specifically, CMB anisotropies are the description of the temperature variations on the microwave sky, i.e. the pattern of hot and cold spots which we can detect using sensitive CMB experiments.
I'm doing my ninth grade science fair project on the theory of a finite, dod
ecahedral universe. ... Most of the words I don't know the meaning of I can do
without, but the main one that I can't seem to get around is "spectrum".
Do you think you
could explain to me the meaning of this word, and what exactly its relationship
to my topic would be?
Submitted by jewelz1088"AT"comcast.net 01/04
Here "spectrum" has a slightly more general meaning than you might have come across. A spectrum is usually the light spread out into all its wavelengths (colours). This might be more properly called the frequency spectrum.
But we can also imagine taking an image and splitting it up into the amplitude of waves in space - we can plot amplitude versus (spatial) wavelength, for example, as a way of describing the information in the image. More usually physicists like to plot the amplitude squared against the inverse of the wavelength, and that's called the "power spectrum". A plot of this power spectrum is a good way of statistically describing the content of an image. In particular it gives a way of seeing how much "power" the image has at different scales (i.e. is it very blotchy on small scales, or large scales, or what?). This is the standard technique for describing the statistical content of CMB maps. For large enough maps (where the sky isn't flat, but curved) you need to use something slightly different, which works on the surface of a sphere rather than on a flat plane, but it's still called the power spectrum.
The point is that theoretical models of the Universe can predict the shape of this power spectrum. And so by careful statistical comparison of the observed power spectrum with a set of theoretical ones, we can infer things about the model which describes our Universe.
Would you be kind enough to tell me who was the first cosmologist to propose
acoustic oscillations (as opposed to density fluctuations)as the origin of the
CMB anisotropies. The more I think about it, and the more I'm convinced it is
one of the most brilliant ideas in the whole field of modern cosmology!
Submitted by georges_melki"AT"hotmail.com 02/04
This is an excellent question!
The main idea is that density perturbations oscillate as sound waves, driven by gravity and with the restoring force provided by pressure between the baryons (regular matter) and photons. The CMB sky can be thought of as a snapshot of these oscillating modes - kind of like a set of standing waves with random phases, spread over the sky. The evolution of the sound waves makes particular angular scales special, resulting in the peaks and troughs seen in the power spectrum of CMB anisotropies.
The best answer is that the idea was already fairly clearly formulated by Jim Peebles and Yacob Zel'dovich (and their collaborators) around 1970. There are papers by these US and Soviet groups about that time which show power spectra with such oscillations present. At that time there was most focus on the signature of the oscillations on the matter disctribution (non-baryonic dark matter wasn't really talked about then!), but over the next few years there were published predictions of CMB anisotropy power spectra too. Particularly important papers with such predictions were those by Doroshkevich, Zeldovich & Sunyaev in 1978 and Silk & Wilson in 1981. Precisely which paper contained the definitively earliest prediction of the CMB acoustic peaks is probably a matter which will be debated by future historians of science!
The idea for acoustic oscillations at all in the Universe goes back to Andrei Sakharov (also famous as a dissident) in the mid-1960s. However, Sakharov's picture was of a cold universe, since this was before the CMB had been discovered. Hence there were no anistropy oscillations in his picture, since there was no CMB at all!
Some people like to give some of the credit to Sakharov. But my own view is that although he played an important role, the real progress was made by Peebles, Zel'dovich and co., when they formulated the modern ideas around 1970.
Could you pls elaborate on the Fourier development of the CMB power spectrum in
your FAQ section.To my knowledge,Fourier analysis applies to periodic functions,
and I can't see anything periodic in the CMB!
Submitted by georges_melki"AT"hotmail.com 02/04
You can certainly carry out Fourier analysis for functions which are not periodic, provided that they're bounded. For example, if you have an image of something in a rectangular array of pixels, then you can Fourier transform the image to understand the amplitudes of all the waves (which fit to have nodes at the boundaries of the image) that you have to add together to contruct the image. In 2-dimensions you can separate the problem into waves in the x-direction and waves in the y-direction. If there's no special direction in the image, then the information in the 2 directions will be statistically the same, and you'll care about the amplitudes (and possibly phases) of the modes as a function of the modulus of the vectors in Fourier space.
The analysis of CMB images is exactly the same, at least for small maps. There are no special directions in the CMB sky, and the phases of the CMB anisotropies are random (this is both justified from theoretical prejudice and from empirical testing of real CMB data). So you can statistically describe the structures in the map by looking at the power spectrum of Fourier modes, i.e. estimates of the squared amplitudes of the Fourier modes as a function of scale (or technically the wavenumber, the reciprocal of scale).
For CMB maps which are larger, you can't ignore the curvature of the sky. So you can't use Fourier analysis, which only work for a flat image. Instead you use a different set of functions to decompose the CMB sky - functions which are appropriate to use on a sphere. These are called spherical harmonics. The CMB power spectrum is plotted as a function of "multipole", which is an inverse angle. This is simply the curved sky version of the Fourier power spectrum of a flat 2-D image.
was universe really re-ionized ? how to detect it's
signatures on the CMBR. What is means by optical
depth and how to measure it for reionization ?
Submitted by jprasadb"AT"yahoo.co.in 04/04
The Universe became neutral at about 300,000 years after the Big Bang, which is the time the CMB photons last scattered. Except that the Universe became ionized again fairly recently (by cosmic standards) at maybe a few hundred million years after the Big Bang - and this has a small effect on the CMB photons. "Optical depth" is the term used to quantify the amount of scattering. The bigger the optical depth between us and the epoch of reionization, the bigger the effect on the CMB. These effects are measurable on the CMB anisotropies, and give a particularl signal in the large-angular scale CMB polarization data. Such a signal was seen by the WMAP satellite, and through measuring it in more detail we should be able to learn about the processes which reionized the Universe.
so, if the big bang was lumpy, we could see changes in the CMB flux
as time goes on, or if we could go to another point in the universe?
Submitted by rich"AT"concordma.com 07/04
This applies to the lumpiness of the Universe at the "last scattering surface", when the CMB photons last interacted with matter. We see a certain pattern of anisotropies on the CMB sky because of these irregularities. If we could instantaneously move to a different part of the Universe, then we'd be seeing a spatially different surface in the past, and hence see a different pattern of anisotropies. However, you'd have to travel a cosmologically significant distance in order to see much difference! And the amplitudes of the temperature variations as a function of angular scale on the sky (a.k.a. the anisotropy "power spectrum") would be statistically the same as we see on our sky.
It's also true that if we wait long enough we'll be able to see the CMB sky changing, as the last scattering surface moves back through space. But again, you'd have to wait a cosmologically significant amount of time before you'd notice the difference!
I have read some papers,books,reviews.But I can't understand why in angular
power spectrum of CMB the main contribution in low multipoles(l) is mainly due
to SW-ISW effect?I mean t o say that we can explain low "l" contribution to
angular power spectrum conside ring SW-ISW effect,why?
Submitted by kanan"AT"cts.iitkgp.ernet.in 04/05
This is alittle hard for me to answer, since I don't know how much you already understand. But let me have a stab anyway.
"SW" is the Sachs-Wolfe effect, first pointed out in a paper by Sachs and Art Wolfe in 1967. The physical effect is that fluctuations in gravitational potential cause fluctuations in CMB temperature. Basically we can see correlated variations in gravitational potential on the last-scattering surface on a wide range of angular scales. These scales include those which are large enough that causal physical processes cannot have affected them between the time the fluctuations were laid down (the inflationary epoch, say) and the last-scattering time. This corresponds to an angular scale of about a couple of degrees on our sky. So on angular scales measured in degrees we're seeing the "initial conditions" in the variations in gravitational potential, unaffected by causal processes - in other words we see the Sachs-Wolfe effect at low multipoles.
I hope this helps!
At http://snews.bnl.gov/popsci/spectroscope.html it is said that "a
Doppler-shifted blackbody spectrum from a body at one temperature doesn't
look exactly like a blackbody spectrum produced at any other temperature".
Is that statement really correct and does it mean that the Doppler shifted
CMB dipole is not a blackbody?
Submitted by vorleons"AT"hotmail.com 08/05
The CMB dipole does not have a blackbody spectrum, but a spectrum which is the frequency derivative of a blackbody. You can see this by realising that the dipole is the CMB pattern minus the "monopole", i.e. you need to take a difference. For any anisotropy measurement, the function you use to convert from intensity fluctuation to temperature difference is the derivative of the Planck (blackbody) function.
And actually it's a little more complicated that that, since really all we've done by using the derivative of the Planck function is use the first term in the Taylor expansion. In principle higher order corrections are also there, and potentially measurable as small (calculable) deviations from the monopole (times the Planck function) plus the dipole (times the derivative of the Planck function).
If one could actually measure the absolute spectrum at every point (rather than making relative measurements), then of course it would be an exact blackbody everywhere, with the temperature varying with position.
If you'd like more technical details, there's a paper in 2003 by Kamionkowski and Knox, called "Aspects of the Cosmic Microwave Background Dipole", which you can find here
Could you also comment on the accuracy of the following comment in a
Wikipedia article about the CMB (http://en.wikipedia.org/wiki/CMB): "There
are however very small yet significant variations (anisotropies) from the
black body spectrum. The most pronounced is the dipole anisotropy (180
degree scales) which is at a level of about 10^−3 of the monopole." I
thought that no spectral deviation from a blackbody has so far been detected
in the CMB and that those anisotropies are just temperature variations from
point to point.
Submitted by vorleons"AT"hotmail.com 08/05
I wonder who wrote that?!
I think it should say something like "There are however very small yet significant variations (anisotropies) from the uniform temperature observed on the sky".
Maybe you'd like to edit the wikipedia entry? You're obviously smarter (or at least more careful) than whoever is responsible for that statement!
[Abridged] ... whereas they go into elaborate mathematical developments, there
is always something arbitrary on the physics side(or so it seems to
me at least).Take for example Zaldarriaga's "An Introduction to CMB
anisotropies", which I find excellent regardless of the numerous
typos.Here is a typical statement from this paper:
"We start by considering perturbations produced by density
modes.When working with linear theory in a flat universe, it is
convenient to use Fourier modes because they evolve
independently.These modes are the eigenfunctions of the Laplacian
operator.."
Well, apart from the last statement, which is trivial[exp(ik.x) is
definitely an eigenfunction of the Laplacian...], all the rest
seems to me to be imposed on the reader! To start with, I don't
agree with the "flat universe" bit,it is misleading:the universe
may be spatially flat...
Then,why is it convenient to use Fourier modes to describe density
perturbations?Because they evolve independently? And how do we know
they are the only modes?Is this a postulate?
A few pages further, we have another "deus ex machina"
statement:"The anisotropy field is characterized by a 2x2
tensor".Again, what is the reason for this?
Submitted by brans_dicke"AT"yahoo.com 09/05
All of those statements seem pretty obvious to me, but then I was trained as a physicist and not a mathematician!
When we say the Universe is "flat", we mean that its spatial sections are Euclidean. That's a very good approximation in the early Universe, since it's pretty much true today and all the models evolve away from flatness.
The Fourier modes are a complete set of modes. In other words I can write down any scalar function of position (describing the density field) and construct it as a superposition of 3D Fourier modes.
It's convenient to use Fourier modes, because they evolve indpendently in "linear perturbation theory". Linear theory is a very good approximation at early times since the dimensionless amplitude of the perturbations is about 10-5.
And the business of the 2x2 tensor, that's for describing the full polarized CMB anisotropy field. The reason for this choice is just geometry - that's the mathematical object you need to describe the algebra of linear polarization. You can look this up in standard textbooks on polarization - there's nothing about this which is specific to the CMB.
I hope this helps to dispell at least some of the apparent acts of faith!
In a nut-shell, CMB anisotropies can be thought of as the line-of-sight
projection of various plane-wave temperature and polarization
fluctuations.
Amazingly, the acoustic peaks are due to contributions in a direction of
observation which is orthogonal to the wave-vector.
Isn't there a paradox here? And how do you explain this?
Submitted by georges_melki"AT"yahoo.com 10/05
You're right. Except that the "spatial" part of the phases of the plane-waves is completely random (to a high degree of accuracy at least). So you can think of a sea of fluctuating lumps, whose specific positions aren't organised in any way (or alternatively think of a set of plane waves with all sorts of directions and random positional phases). It's the "temporal" phases of all the fluctuations which are coherent, i.e. all the lumps of a particular scale are oscillating in and out together, like balloons being inflated and deflated (or like a set of standing waves if you're thinking in the wave picture).
The CMB "last scattering surface" is just like a slice through the 3-dimenstional distribution of lumps at a particular time. There are places (in space, or projected on the sky) where the amplitude is high (both positive and negative) and places where it's low. But on a particular scale they're all evolving together in time. So the variance of the amplitudes of the fluctuations is just a function of time, for a given scale. Now if we take a snap-shot of the pattern, we see this variance being a function of scale, which we measure as the angular spectrum of the CMB anisotropies. And it doesn't really matter whether you think of this scale as being in the line-of-sight direction or the transverse direction, because there are no special directions in the Universe.
could you please explain why the fluctuations in CMB map produced by the
WMAP satellite allow cosmologists to observe structure in the universe further
back in time than do observations of galaxies at high red shifts.
Submitted by Lilac4moi"AT"aol.com 10/05
When we see the CMB, we are seeing the structures in the Universe at the time the photons were last scattered. This turns out to be about 300,000 years after the Big Bang. The CMB photons have been stretched by a factor of about 1000 since that time, i.e. we're observing back to redshifts of about a thousand. So by measuring the CMB anisotropies we can learn about the structure in the Universe at very early times, when the density contrasts were still low (i.e. before any actual objects had formed).
When we observe galaxies, we're seeing the photons that were made in stars in those galaxies. The most distant galaxies are seen at redshifts of about 6 - and obviously most galaxies we see are at much lower redshifts than that. So we know a lot about structure in the Universe are relatively low redshift. Obviously you can't see galaxies unless there's starlight, and we think the first stars were formed at redshifts below 20 (although this value is still very poorly known). Se we're never going to see individual galaxies back to redshifts anywhere like as high as where we're seeing the CMB anisotropies.
The neat thing is that by comparing the structure at low redshift with the structure at earlier times seen on the CMB sky, we can learn a huge amount about how structure has formed in the Universe.
In an article by Hu and White entitled "A CMB polarization primer", one
reads the following statement:"The degree of linear polarization is
directly proportional to the quadrupole anisotropy in the photons when
they last scatter".
So, is this the same quadrupole that gives the differential background
temperature between two points on the sky separated by 90 degrees?Or is
it some property of the radiation at every
point in the sky?
Submitted by georges_melk"AT"yahoo.com 10/05
It's both of what you suggested.
Every observer in the Universe sees their own last-scattering surface. You can also think of the scatterers on our surface seeing their own "sky". On that sky there will be a quadrupole, and this is what acts as the "source" for the polarization. The polarization we observe is the sum over all the patterns made by all these scatterers.
I have - on a number of recent occasions - received conflicting information
regarding red spots versus blue spots on the CMB. For instance, in a webcast
lecture at the Space and Telescope Science Institute, Rachel Somerville
describes the red spots as being hot along with having high density
characteristics. In contrast, she describes the blue spots as being cold along
with having low density characteristics. Therefore, Dr. Somerville argues that
the high density, red spots are a reflection of photons falling (collapsing)
into gravitational wells, in effect, contributing to this red "high density"
signature. On the other hand - in a webcast lecture at Perimeter Institute -
Rachel Bean describes reds spots as being hot yet having properties of low
density. In contrast, she describes the blue spots as being cold yet having
properties of high density. Therefore, Dr. Bean argues that low density, red
spots are a reflection of photons escaping (expanding away) from gravitational
wells, in effect, leaving behind a "low density" signature. In other words,
Someville's red spots are correlated with high density and the "contracting
dynamics" of the photons falling into gravitational wells. In contrast, Bean's
red spots are correlated with low density and the "stretching dynamics" of
photons escaping from gravitational wells. Is this a simple case of one
scientist being right while the other being wrong? Or is this a more complex
case of both scientist being right? If this is a typical example of
duality/equivalence in physics where Nature can be expressed separately yet
equally on two sides of the 'same coin of reality," please enlightened me on
how both scientist can derive these contradictory yet correct conclusions.
Despite my obvious naiveness regarding the broad yet convoluted subject of CMB,
I am - needless to say - receptive to a response
Submitted by cynholt"AT"bellsouth.net 12/05
So this is a battle of the Rachels!
I believe that Rachel B. is (largely) correct here. Although Rachel S.'s confusion is entirely understandable.
For a start, the colours are completely arbitrary! It just depends which colour-table you choose. Physically one might have imagined that red would be cool (because of redshift) and blue would be hot (because of blueshift). But that disagrees with the "bathroom tap" convention, i.e. members of the general public (who aren't usually physicists) "know" that red things are hotter than blue things. So the COBE DMR team chose to use the "bathroom tap" convention, where red is hot and blue is cold. And many other CMB map-makers have adopted the same convention.
The next complication is that there are several different physical effects happening. If we restrict ourselves to the largest angular scales, then things are probably the simplest. Here we have a combination of "intrinsic" temperature fluctuations and gravitational redshifts/blueshifts. A region which is overdense in gravity will be overdense in both matter and radiation (this is a consequence of the perturbations being of the "adiabatic" sort typically produced in early universe inflationary models). This means that an overdense region is also hotter (redder). However an overdense region is also hard for photons to climb out of, i.e. there's a gravitational redshift, and so the radiation appears cooler (bluer) to a distant obsever. It turns out that the gravitational redshift has a bigger effect that the intrinsic temperature variation (see the question: "Where does the 1/3 come from?" on my "Advanced FAQs" page), and hence overdense regions appear cooler than the average (and hence blue). The same is true for underdense regions, which appear hotter than average (and hence red).
On smaller angular scales things are less clear though, because the effects of oscillations compressing and rarefying the material can be larger than the gravitational redshifting effects, but these depend on scale. And there are additional effects due to velocities (i.e. Doppler shifts), as well as lots of other effects as one goes to even smaller scales.
So on large scales hot spots are underdesnities and cold spots are overdensities. But on smaller scales the best answer is "it depends"!
After checking
your faq page, I still have doubts about the precise
relation between CMB anisotropies and the Cosmological
Constant (and dark energy). I would be very glad if
you could also provide me some graduate/post-graduate
level bibliography on the subject.
Submitted by alice.holden"AT"yahoo.com 06/06
Dark Energy mainly affects the evolution of the Universe at low redshift (i.e. relatively recent times). So there is little direct imprint on the CMB sky, since the anisotropies are mainly formed around a redshift of 1000 in the fairly early Universe. But what Dark Energy does affect is the distance to the last-scattering surface, which changes the angular structure of the CMB anisotropies. Precise measurement of this angular structure gives an accurate value for the last-scattering surface distance. This in turn gives a constraint on how the Universe has been evolving. Combining this with any of a number of other cosmological constraints (e.g. the measured amount of Dark Matter) then gives a good estimate to the amount of Dark Energy. The fact that this compares very well to what is inferred from observations of distant supernovae is the main reason why Dark Energy is taken so seriously.
You can find much more technical discussion of this and related issues in my article with George Smoot, a pdf version of which is here
Some very basic questions, perhaps an omission in my physical knowledge.
What is meant exactly with one part in 100.000?
What is angular scaling (degrees) in relation to the band filtering of a
piece of the CMB map, I don't understand the proces of transgression of
only 2 coulors (low L or many degrees) tot a whole colour mosaic (several
100 L's or 1 degree)?
What is the practice of measuring the temperature differences in every
scale, I mean do they use a standard distance between points or is it a
mean diifference between hottest and coldest points in evere scale or is
it totally different?
Submitted by rulf0000"AT"planet.nl 07/06
"One part in 100,000" (or equivalently 10-5) is a way of saying that variations in the CMB temperature (in this case) are at the level of 1/100,000. In other words, since the CMB temperature is 2.725K, then the temperature variations are at the level of about 30 micro-Kelvin.
I'm afraid I don't really understand your second question. But it suggests that you've been looking at CMB anisotropy maps (from the WMAP satellite for example) and trying to relate those to the "power spectrum" of Cl. To fully appreciate that, you need to understand what a "Fourier spectrum" is, and then how to extend that idea to a curved sky with "spherical harmonics". But the simpler version is that CMB experiments measure the "variance" (i.e. statistical scatter) in a CMB map, and they do that as a function of different smoothing scales. You can think of the Cl plots as depicting this variance as a function of angular scale of the smoothing, with large smoothing corresponding to small multipole "l".
Your third question is related to the second. The quantity measured is essentially the variance, i.e. the average of the squares of the differences from the mean temperature in the map.
I measure the temperature at one point on the sky [ mean temperature on a
small surface- pixel] , than on another point with angle alfa between
these points. I do it many times on the whole sky and make average of
this difference of temperature. Than I repeat the procedure with
different angle and so on. I have function- difference of temperature viz
angles. Now mathematica machinery Legendre transformation and spherical
harmonics and POWER SPECTUM ! Am I right ? [ Of course it is only great
lines of reasoning.]
Submitted by skarbzbig"AT"neostrada.pl 08/06
I think you've got it!
Although to correct you a little, it's the variance among the set of pixels that you measure. First remove the overall CMB temperature from the whole set of pixels, then calculate the average of the product T(i)*T(j) for positions "i" and "j" separated by some fixed angle. Then do this for a whole bunch of different angles. This gives you the "correlation function" of the CMB sky as a function of angular separation. Finally, the "power spectrum" is the "Legendre transform" of that!
Just reading through the CMB FAQ and came across the question on
Anisotropy and its pronuniciation. I have found that a phonetic
pronunciation helps me to pronounce certain words. I looked up
Anisotropy on www.dictionary.com and found this pronunciation:
an-ahy-so-truh-pee
Submitted by jg318206"AT"att.net 10/06
Seems pretty good to me! Thanks.
My question is this:If the basis for the measurements is looking at "dark
spots" in the Universe. How can we be sure that the areas we are looking at
is dark.
When the Hubble telescope was aimed at a dark spot in the universe it found
1000 galaxies.
So are the dark spots used for the microwave background radiation readings
.... dark ?
Submitted by ericfarmer"AT"adelphia.net 6/07
I'm afraid that this is one of those times when an attempt to simplify an explanation only results in more confusion!
The CMB sky is described by a set of measurements of temperature variation at different sky positions, or equivalently a set of brightness measurements for those positions at microwave wavelengths. There are variations all over the place, however the map of the CMB sky is quite unlike most other astronomical images: the contrast level between "hot spots" and "cold spots" is really very low, and there are no well-defined "edges" to any features. So it's not very helpful to speak about specific shapes on the sky, "dark spots" for instance. Instead one needs to statistically describe the average contrast level for different sized features. This is techincal called the "power spectrum of anisotropies". And it is this power spectrum that encodes the information which tells us what sort of universe we live in.
It appears that whatever you were reading was trying to describe this statistical pattern by saying that CMB experiments detect "dark spots" and "bright spots". But these have nothing to do with visible light, they are also quite ill-defined (since it depends what angular scale you are concentating on), and in any case they are only variations ati the tens of micro-Kelvin level compared with the roughly 3 Kelvin temperature of the CMB sky as a whole.
Since the dipole moment is observer-denpendent and could be removed if
we choose an appropriate coordiante. But this dipole velocity still plays
a cruitial role in the theoretical studis of the acoustic peaks. For
example, in W. Hu and S. Dodelson 2002 , the continuity equation includes
the photon velocity which can be treated as the dipole velocity. Why does
this removable dipole still underlies the anisotropic spectrum? Is this a
coordinate-choice problem?
Likewise, the monopole is the mean temperature of the CMB. They say
"The temporal and spatial variations of the monopole and dipole determine
the anisotropic pattern". How to understand this?
Submitted by richard.loogn"AT"gmail.com 7/07
This is a genuinely hard technical question!
There are some subtleties here, but the monopole and dipole are certainly observable - the complication comes when you think about how this relates to causality, choice of coordinates etc. In fact I'm working on a paper right now with some colleagues on this very topic. So look out for that in the next few weeks. [This is a long-winded way of saying that I don't really know the answer!].
As to the damping tail on the anisotropic spectrum, yous review 2006
says that this damping tail can be explained by either the finite
thickness of last scattering surface, or the imperfect coupling of the
photon-baryon fluid. Does this mean that we really don't know which is
the true reason, but just model-fittings?
Submitted by richard.loogn"AT"gmail.com 7/07
Another technical question! We know that when we put the right physics into a computer, then the damping tail comes out, i.e. we see less and less anisotropies at the smallest angular scales. So there's no real mystery about what causes this. The issue is how does one describe the basic physical reason behind the effect, and the answer is that there's more than one thing going on, and more than one way of looking at some of the effects too. If you want the gory details, then read the 1997 paper by Wayne Hu and Martin White, which you can find here.
I am just finishing a set of small sky charts ...
These charts show the positions
of important objects on the sky, for students who want to find these
objects. He has requested two charts showing the positions to which, and
from which, we appear to be moving within the CMB from the small
temperature asymmetry for the Cosmology chapter. These positions are
labelled Leo and Aquarius respectively in textbooks. However, unless we
are missing something vital, neither the WMAP or COBE pole positions are
within these constellations, nor is your quoted (Scott and Smoot) position
after correction for solar system motion. Is there some "historic" reason
why these names should be applied to these pole positions?
[abridged]
Submitted by taclark"AT"ucalgary.ca 9/07
The "dipole" of the CMB has a very well defined direction - but the issue is what reference frame do you want to specify for that motion?
The direction of the dipole that we measure gives the speed of the Earth (or a satellite like WMAP, which is pretty much the same thing) relative to the CMB. Typically you would remove the variation caused by the Earth's motion around the Sun (which has a ~30km/s amplitude and a 1 year period). Then you're left with the motion of the Sun (or the "Solar System barycentre" if you like) relative to the CMB. That could certainly be said to be "the dipole" and hence you could indicate that direction if you want. But the Sun's motion around the Milky Way Galaxy is a big part of that, is quite well known and isn't really very "cosmic" - and so if you want to know the Milky Way's motion relative to the CMB, then you'd subtract off the Sun's vector (which is about the same magnitude as the overall dipole and in roughly the opposite direction). Then you get the ~600km/s value that's usually quoted as "our motion through the sea of CMB photons".
I think the Solar-CMB motion is perhaps in the direction of the constellation Leo (but just at the southern edge), while the better "Milky Way" or "Local Group" dipole is further south, maybe in the direction of Hydra. The direction that we're moving away from in the "cosmic dipole" is whatever is on the opposite side of the sky from that.
I was reading your CMB FAQ page
(http://www.astro.ubc.ca/people/scott/faq_basic.html) recently. I do not
understand your answer to "How come we can tell what motion we have with
respect to the CMB?" It seems to me that the CMB photons are traveling
at speed c relative to us and relative to any other frame in the
universe. There is no frame in which light is at rest. If you could
explain to me what I am missing here, I would appreciate it.
Submitted by ceciliavogel"AT"augustana.edu 12/07
You're right that the CMB photons are travelling at the speed of light no matter what frame you're in! However, there are measurable effects of your motion.
The correct way to work this out is to calculate the effects of a "boost" within the theory of Special Relativity. But I'll dispense with the full mathematics here, since you can understand the basic physical effects quite simply.
Just imagine that you're surrounded by a sphere of people pointing flashlights at you - this is a crude model of the Universe! Now, if you move reasonably quickly in some direction then there will be several noticeable effects. Firstly all the photons in the direction you're moving towards will be blue-shifted (higher energy), while those in the opposite direction will be red-shifted (lower energy). But also the flashlights in the direction you're moving will appear to be denser together on the sky than those in the opposite direction (that can be understood because you're travelling to "meet" the light rays at a slightly different angle).
The net effect of all this is that you will see a "dipole" pattern on the sky, i.e. more brightness for one "pole", smoothly varying towards less brightness at the other "pole". All of the photons are moving towards you at the speed of light, but you can still tell your motion relative to the "rest frame". In CMB language that means we can measure our motion through the Universe relative to the "CMB rest frame". Here the phrase "CMB rest frame" just means "the frame in which there's no CMB dipole".
I hope this has helped demystify this issue for you!
My question is: why are there two dots, presumably at the apex and antiapex of
the sun's motion, in the COBE map in today's APOD?
(http://antwrp.gsfc.nasa.gov/apod/ap080309.html)
They make it look like a stretched yin-yang symbol. If I'm interpreting the
colors right it look like at those points the temperature is a little cooler
than in the adjacent regions. My guess it is some artifact of the measuring
process and not a cosmological feature, but I couldn't find out any mention of
the features much less an explanation.
Submitted by jjb"AT"vt.edu 03/08
This is an image of the microwave sky made by the COBE satellite, with temperature (or brightness) colour coded, with warmer parts being red and cooler parts being blue. It is a map of the whole sky projected onto an oval shape, with the Galactic Plane running horizontally across the middle, the Galactic North Pole at the top and the Galactic South Pole at the bottom. The image has had the average temperature removed, so that this is a map of temperature differences relative to the average. Apart from that though, it has had nothing removed.
The "yin and yang" shape is the "cosmic dipole", which is caused by our motion through the Universe. We see the CMB being a bit hotter in the direction we're moving, and a bit colder in the opposite direction, with a gradual variation in between.
The other stuff that you see in the image is from the Milky Way Galaxy that we live in. Parts of the Milky Way are brighter than others, and at these wavelengths the brightest parts are about as bright as the dipole.
Those spots that you see are parts of the Galaxy, along the middle of the image. When one wants to study the "anisotropies" from the distant Universe, the Galaxy gets in the way. Despite the best efforts (by observing at a series of different wavelengths, for example) it's not possible to completely remove the effects of the Galaxy, and so for studying the distant Universe a horizontal strip is cut out of the image, and the dipole is also removed. Then the much fainter primordial anisotropies are revealed (as seen in other maps from COBE or WMAP, for example) - which tell us so much about the Universe.
I understand there was a mathematician collaborating with Einstein at
Princeton who speculated, based on his work, that the Universe was/is
essentially rotating and not expanding, it's just that the scales are so
large that our thinking is being influenced along the lines of a more
simplistic and linear perspective for purposes of social interaction.
Possible?
Submitted by jmar55"AT"yahoo.com 03/08
The Universe could certainly be rotating in principle. There are a set of cosmological solutions to Einstein's field equations which have rotation, specific examples of what are called the "Bianchi solutions". However, these models predict specific patterns of anisotropies in the CMB, which are not seen. Hence one can place very tight limits on the amount of rotation.
I was
wondering what the new total mass-energy density parameter [omega.uc.gif]
tot was from the most recent 5-year WMAP data.
Submitted by jeffakkerman"AT"yahoo.com 07/08
If you are asking about the mass contribution in matter, the value decreased slightly compared with the previous data. The new value is 0.24 +/- 0.03. But if you are asking about the "total" (including the Dark Energy), then the answer is still consistent with unity, with an error bar which is only 1 or 2 per cent. This means that the Universe appears to be quite close to "flat", i.e. like good old-fashioned Euclidean geometry.
on your page http://www.astro.ubc.ca/people/scott/faq_basic.html, you have a
question under the header "How come we can tell what motion we have with
respect to the CMB?"
I should say I'm no physicist and it was the first time I read anything
substancial about CMB. But the above question intrigued me. However, reading
your answer I didn't get any wiser. In fact, I have a feeling that something
is missing or assumed in your answer.
You write that "in the CMB rest frame you measure no velocity with respect to
the CMB photons". There is something weird in this statement for a physics
noob like me - from the little I have read about physics, that sounds alot
like the idea of an ether to me. You say in many places that the photons move
at the speed of light. How then would it be possible to see them at rest? You
would have to be moving along with them at the speed of light? Secondly, you
say that the CMB photons are moving in all directions. How then, can there be
a certain frame relative to which all the photons are at rest? Third, you only
mention the theoretical aspect, "that it is possible", but don't say anything
about how you actually measure it. Measuring the speed of the photons? But
they should all be moving at the speed of light?
Please enlighten me! :)
Submitted by mikael_eriksson76"AT"yahoo.com 09/08
I'm afraid I was being a bit sloppy with language here - sorry that this has confused you.
The CMB photons are always moving at the speed of light. There is a frame in which they are isotropic, in other words you see as many of them coming at you from one direction as any other direction. If you move relative to that frame, then you see more of them coming at you from the direction towards which you are moving and fewer in the direction you are moving away from (it's a bit like running in the rain).
So, to be a little more explicit, the number of photons per square degree (or other unit of solid angle) changes over the sky. This means that the brightness of the CMB also changes over the sky, and we observe the familiar dipole pattern. The direction and amplitude of this pattern tells us how fast we are moving compared with the "CMB rest frame". Here the phrase "CMB rest frame" is short-hand for "frame in which the CMB has no observable dipole, so that the sky is isotropic on large angular scales".
reguarding the cmb,
How does studying the radiation lead to our abiblity to determine the
composition of the universe, ie baryonic vs non-baryonic materials??
Submitted by gx_cully"AT"laurentian.ca 11/08
The idea is that there are variations in the temperature (or brightness) of the CMB sky. The strength of these variations is a function of angular scale. Experiments like the WMAP satellite measure the CMB sky accurately, so that this function can be calculated. The shape of this function (technically called the "power spectrum of anisotropies") encodes information about the initial fluctuations in the Universe and how they have evolved with time, which depends mainly on the composition of the Universe. So by accurately mapping the anisotropies it is possible to derive the values of several cosmological quantities, like the fraction of matter that is in the form of atoms as opposed to dark matter, etc.
Is the dipole anisotropy due to the Sunâs orbital motion about the galactic
center, some motion of the galaxy in the local group, or is it something
bigger?
Submitted by soule1061"AT"verizon.net 10/09
The dipole is caused by the vector sum of all the relevant motions. This includes the "something bigger" which you allude to, namely that the Local Group of galaxies is moving at several hundred km/s towards a particular direction (sometimes called the "Great Attractor"). But the motion also includes the motion of our Galaxy relative to the centre of mass of the Local Group, the Sun relative to the local centre of mass, the motion of the Sun's neighbourhood around the Galaxy, the Earth's motion around the Sun, and even the rotation of the Earth (for a terrestrial experiment).
Kate Land and Joao Magueijo of Imperial College London labeled the dipole
anisotropy the "Axis of Evil". Can you elaborate?
Submitted by soule1061"AT"verizon.net 10/09
The so-called "axis of evil" is not the dipole. Instead it is a particular direction relative to which the largest-scale anisotropies (excluding the dipole) appear to be mildly correlated. I think it's fair to say that most cosmologists regard this is just a statistical fluke (perhaps affected by some systematic mapping effects), rather than an indication of some new physics. The statistical significance of the correlation is not very strong, and has not become stronger as the quality of the data has improved. It will be interesting to see if something similar is seen by the Planck satellite. But if the effect doesn't become more striking then this will get shelved under "interesting quirks" rather than leading to any Nobel prizes!
Why does not in CMB red spot (gravitational blue shift) canceld with blue
spot (gravittional red shift) ? I mean why S-W effect couldn't cencel each
other ?
Submitted by hossein_dod"AT"yahoo.com 01/10
You're right that if a CMB photons crosses a gravitational potential well (or hill) there will be a redshift and blueshift which cancel out, so the net effect on the photon is zero (unless the potential changes a bit while the photon crosses it). But for the "Sachs-Wolfe" effect you're supposed to picture a photon scattering inside a potential fluctuation on the "last-scattering surface". So if it's an overdensity, then there's a gravitational redshift as the photon climbs out, and if it's an underdensity there's a blueshift. So for each photon being scattered there's no cancelling effect.
How could scientists find (calculate) ratio of ordinary matter to dark
matter from CMB (power spectrum) ?
-How could scientists find (calculate) ratio of dark energy to matter from CMB
?
Submitted by hossein_dod"AT"yahoo.com 01/10
The cosmological parameters affect the shape of the CMB anisotropy power spectrum. So by measuring the spectrum accurately and comparing with model predictions, one can tie down the values of the parameters, and combinations of parameters. One such combination is the ratio of ordinary (baryonic) matter to (cold, collisionless) dark matter. Another is the fraction of all energy-density made up by the so-called dark energy.
There are some descriptions of the underlying physics, which can explain how features in the power spectrum are related to the values of the parameters. However, these are only approximate arguments, and for precision there is no substitute for carrying out a detailed statistical comparison. That's what the WMAP team has done, for example, to provide estimates (including error bars) of the quantities that you are asking about.
Is red spot with character size 1 degree on CMB map less dense area ? Why ?
Submitted by hossein_dod"AT"yahoo.com 02/10
Usually the colour scheme chosen is red for hotter and blue for cooler. Although that is really just up to the choice of the person who makes the figure, so it could be the opposite!
On large scales a hot spot is typically an underdense region and a cold spot is an overdense region. But on smaller scales (below about a degree) things are a bit more complicted because of the oscillating sound waves, whose combined effects we see on the microwave sky.
Several years ago (2003) in a review published in a Czech journal called
Progress in mathematical and physical sciences
written by prof. V. Wagner from the Institute of Nuclear Physics, in which was
published the angular power spectrum of the CMB radiation (from paper by
J.L.Sievers et al. in the Astrophysical Journal 2003. 591,599-622). The most
fascinating thing for me was that this spectrum has a remarkable similarity
with the scattering spectra of X-rays or neutrons measured on disordered
materials [abridged]
Submitted by L.Cervinka"AT"icaris.cz 04/10
It is interesting that there is some similarity, and so it might be that one could investigate the level to which there is a physical analogy here. However, this can only be an analogy, since the physical processes are completely different, e.g. the scattering process, length scales involved, linear theory fluctuations vs highly non-linear solids, etc.
I was not able to find any kind of information on
atomic/particle distances deduced from some other analysis as well as
corresponding particle density data. I have found in your FAQ that there is a
density of 412 photons and 2 x 10E-7 baryons per cubic centimeter, however,
corresponding to the present-day temperature of the universe 2.73 K. Because
the last interactions of CMB photons were realized 300,000 years after the
big-bang when the temperature of the universe decreased to 3000 K, my
extrapolations are done for the wavelength of CMB photons ~1000 nm. My opinion
has been that THIS is the typical wavelength (corresponding to the peak
intensity of the Planck distribution) of the CMB photon. For the present-day
temperature 2.73 K the peak wavelength should be 1 mm. So, which is the
wavelength of the CMB photon bringing us the information on variations of
density at a time of about 300,000 years after the Big Bang when the
temperature has been 3000 K?
Submitted by L.Cervinka"AT"icaris.cz 04/10
The temperature was about 1000 times higher at that epoch, and the density was about (1000)3 times higher (so the average distance between particles was 1000 times smaller).
What is axis of dipole anisotropy of CMB?
Submitted by n_homaiefar"AT"aut.ac.ir 12/10
The dipole is the "two pole" pattern on the sky, due to our motion with respect to the "rest fram" of the CMB. As a result of this motion the sky is hotter in one direction and colder in the other direction, the amplitude being about 1mK.
The precise direction of this motion depends on what detailed question is being asked. There is actually no "absolute rest frame", and hence one is allowed to add (or subtract) any component of our veolocity vector. So the dipole due to the Sun's motion has a large contribution from the Sun's orbit around the centre of our Galaxy - but this is often subtracted out. The dipole vector of the "Local Group" is quite different than the solar motion dipole, for example.
In addition one has to define the coordinate system on the sky. This could be Galactic coordinates, equitorial coordinates, or something else.
Given in Galactic coordinates, the Local Group motion is about 600 km/s in a direction of about (275°,30°).
Re:
The CMB isn't a source of dust. Rather, the dust in our Galaxy acts as an additional signal that we see in front of the Cosmic Microwave Background. So an experiment which is designed to study the CMBB will also study these "foregrounds" - which are interesting in their own right.
I have a question regarding the CMBR.
I have been reading Lawrence Krauss's book - A Universe from Nothing.
My question is:
Page 45 shows a diagram of the Last Scattering Surface (LSS). Could you
please explain the significance of the "1 degree" on the LSS as observed
from earth and why this angle corresponds to 300,000 light years? Why choose
this angle - and why does it corresponds to a flat universe?
Looking at the triangle in the diagram, the text on page 50 refers to the
known distance between us and the LSS as being more than 13 billion years
(which seems sensible). However, with an angle of 1 degree and one side of
the triangle being 300,000 light years, doesn't this imply that the distance
is approximately 17 m light years"
If you can help, that would be fantastic!
Submitted by rslailey"AT"bigpond.com 05/13
Hey, why don't you ask Lawrence Krauss?!
But seriously, although I haven't read that book in detail, and don't have those pages in front of me, I think that's a pretty standard diagram, and so I can probably guess what is going on.
This is like some kind of giant "triangle test" which is essentially how the CMB anisotropies can be used to gauge the geometry of space (it's not exactly what's actually done, but this triangle is the gist of the physics). The point is that we know a specific length scale at the epoch of last scattering. This is the distance that a sound wave can have propagated in the time from t=0 until last-scattering, which is about 400,000 years later. Sound waves in a relativistic fluid travel a bit slower than the speed of light, but let's not quibble about small factors: the length is something like 300,000 light years.
Since we know this length in physical units, we can look to see what angle it is on the CMB sky, This is the "fundamental" mode of the oscillating acoustic waves, and hence is basically the characteristic scale of the blobs in a map of CMB anisotropies. In angle this turns out to be about 1 degree. But since the Universe has expanded by about a factor of 1000 since that time, then length scales are all 1000 times bigger today. So when you compare this length to the distance (which is something like the age of the Universe in light years) you find that about 1 degree works!
Although this sounds a bit hand-wavey, actually the real calculations are extremely precise. So precise that when we compare the anisotropy pattern we find that the Universe has to have "flat" geometry to better than 1% now.
At CMB recombination (z=1090), what is the radial extent of the last
scattering "shell"?
a) Delta(z) = ....
b) Delta(comoving angular distance)= ....Mpc
The WMAP first-year parameters give
Delta(z) = 195. Is this still correct?
Submitted by rhkail"AT"gmx.net 08/13
That's a much more technical question than I usually get!
If you read the new Planck papers, you'll see that the changes in the parameters of the standard cosmological model are really fairly modest. There certainly are significant improvements in the uncertainties, but you have to care about details in order to notice the changes in the best-fit central values!
So the thickness of the last scattering surface is essentially the same as it was from the WMAP satellite results.
I have come across references to the B-mode curl was somewhere around
0.2 something --- what exactly were they referring to?
I also came across some articles quoting scientists saying "we were
looking for a needle in a haystack but we've found a crowbar" meaning that
the amplitude of the findings were greater than expected. What amplitude
(or parameter) are they talking about?
Submitted by webmaster"AT"chapmanhilton.com 05/14
What you're talking about is the parameter usually called r, which is the ratio between two particular kinds of "lumpiness" in the Universe. More specifically, at early times (e.g. during the inflation process in the very early Universe), quantum fluctuations generated variations in density and also primordial gravitational waves. The ratio of the amount of fluctuations in gravitational waves to the amount in ordinary density variations is this quantity r.
The way to try to measure r is to look for tell-tale signs of the primordial gravitational waves, and the best way to do that is throught the so-called "B-modes", which are a kind of "curliness" to the pattern of polarization observed on the CMB sky.
Different models for inflation give different values of r, and hence a measurement of r will potentially tell us something about the physics of the first 10-35 or so. No one really has a clue what to expect for r, but the results from the BICEP-2 experiment appear to give a higher value than seemed compatible with other (less direct) CMB constraints.
When I went to talks or read books about modern cosmology, people would
always refer to the beautiful fitting curve of the best-fitting Lambda CDM
model with the WMAP data. But
I could not find what this model exactly is, apart from there are 6 major
parameters. It is very puzzling how the patterns in the observed power
spectrum which predict the 6 parameters in the model could make such a nice
curve?
So my naïve question is: *What is/are the mathematical equation(s) of this best-fitting Lambda CDM model? *
Submitted by huoguofen"AT"gmail.com 06/14
It is indeed puzzling that a model with just 6 parameters fits the data so beautifully! That's why cosmologists believe we actually understand the large-scale Universe so well.
The data are the "power spectrum", which is effectively like the variance in temperature as a function of angular scale on the sky. The theoretical prediction comes from calculations of how oscillating sound waves evolve in the Universe. This depends on the initial conditions (amplitude and sclae-dependence of the power as a function of scale), together with the amount of dark matter, dark energy etc. (that determines the way that the Universe expands). There are more detailed discussion of parts of this picture elsewhere on this web-page!
When next you
get time please elaborate on CMBR "stretch marks", what they mean, what
became of the 2014 purported discovery of these stretch marks which other
cosmologists seem to later discredit.
Submitted by pd.delwaar"AT"gmail.com 01/15
I confess that I haven't heard this phrase before. And I can't say that I really like it!
"Ripples" in the CMB, what the experts call "anisotropies" are imprinted by variations in density (and other physical quantities) at the time the CMB photons last scattered. And their statistical properties tell us what kind of Universe we live in.
One particular kind of signature in these anisotropies are the so-called "B-modes" in the polarization of the CMB sky. I assume that this is what you are asking about. This is a really weak signature, and very hard to detect - although it is a subject of intense focus, because in principle it can tell us about the Universe at extremely early times. In March 2014 the BICEP2 experiment made such a measurement, and claimed that they had seen evidence from primordial gravitational waves, perhaps coming from inflation. However, the Planck Collaboration (of which I am part), showed that the B-mode signature coming from dust in our Galaxy is stronger than some people had previously estimated. Hence one cannot ignore these "foreground" polarization signals when trying to measure the primordial signal. But many experimental teams (including Planck) are continuing to work hard on this.
I am new to this field ,i want to learn everything about cmb right
from the beginning.I had GTR and cosmology courses in my previous
semesters. Also I have installed CAMB I don't know many of the parameters
used to get the data. So if you can help me by giving some references it
will be great.
Submitted by vipin"AT"iiserb.ac.in 09/15
The CAMB code (which you can find here) is quite well documented and described, including a readme file. More technical details are discussed in papers that you can find in the bibliography on that same web-site.
For a general (but still high-level) introduction to the cosmic microwave background, you might want to start with the review article I wrote with George Smoot, which you can find among the review articles on the Particle Data Group web-site (there may be an updated version by the time you read this). I hope this helps!
As I understand, the CMB is a snapshot of the universe at 380,000 years when
temperature reduced to 3000K and so recombination could occur. However this
led to the problem of the evenness of the CMB as the photons could not
interact and inflation was proposed to resolve this.
Q. If the universe cooled faster than expected, for example reaching 3000K after only 3800 years, could this explain the evenness without resorting to inflation? If so, could you estimate at what age should the CMB be in order that we may dispense with inflation? Are there any models that support this?
Submitted by email4malcolm"AT"yahoo.com
This is an interesting question. But I think it misses the main point of inflation. It's true that in the early days one often-discussed idea was that inflation solved the "horizon problem", i.e. it helped smooth out the observable Universe, making the CMB sky more uniform. However, at the same time the quantum fluctuations generated during inflation can become the seeds for all the structure in the Universe today. You can get that while the CMB sky has "anosotropies" at the level of about one part in 100,000 (that subsequently grow in contrast through gravity).
So the real value of inflation is not that it smooths the CMB, but that it gives a simple explanation for the generation of the variations on the CMB sky (and around us today). And it gives us a picture that allows us to have those density perturbations on all the scales required. I would say that without inflation we have no idea for how to do that. That's not to say that we know inflation happened, but it is a very appealing idea, and it seems reasonable to imagine that whatever the final anwser turns out to be, it will contain parts of the inflationary paradigm.
Could the CMB signal be converted into a Fourier or 2-D Fourier:
"I hope I'm getting this right"
Could the math behind
this video
be used to create an Image from the CMB?
Submitted by unclekel"AT"hotmail.com
That's a good question, and the answer is that you're definitely thinking along the right lines to analyse the CMB!
You can indeed use Fourier analysis for studying the "modes" that make up a patch of the CMB sky. But when the patch becomes large enough, you need to use a system of functions that works on a curved sky, rather than a flat plane (or more generally on a sphere). These are called "spherical harmonics" - but they're really just like Fourier modes for data on a sphere.
The important information in the CMB sky comes from the squares of the amplitudes of these spherical harmonics. The phase information in the modes carries no useful information (or at least hardly any) - which makes the CMB entirely unlike most images that you might take s 2D Fourier transform of, where in fact most information is in the phase correlations. For the CMB these phase correlations are essentially zero, and so we just study the squares of the amplitudes, which is also known as the "power spectrum". The variation of the power spectrum with the parameters of the cosmological model can be used to figure out what kind of Universe we live in.
Can you describe the significance of the Canadian BAM experiment?
Submitted by barrys"AT"creation.portal.ca
BAM is the Balloon-borne Anisotropy Measurement, an ongoing effort to measure the CMB anisotropies, headed by Mark Halpern at the University of British Columbia. The first thing to say is that Mark's experiment is an incredible tour-de-force, given the resources he's had! Compared with US colleagues, the funding for BAM is very modest, and it's enormously to his credit that he has ever flown a balloon. The 1995 flight was largely a success, although there were some minor problems. The result is a significant detection of a signal which is most easily explained as being primordial. BAM's relatively wide frequency coverage means it can do better than most experiments at separating the primordial signal from the local (ie Galactic) signals which get in the way. So the BAM results are certainly among the most reliable indications that there really are primordial fluctuations at angular scales of a few degrees.
Detecting temperature differences of 1 part in 100,000 is pretty difficult! But to make real progress in understanding the Universe as a whole, it is important to measure those fluctuations over as large an amount of sky as possible. BAM is essentially ready to fly again, and is awaiting the return of stable winds to the balloon-launching facility in Palestine, Texas - this won't happen until about May, so that is when BAM is due to fly. This next flight will have increased sensitivity, and several other improvements, making it possible to scan a much larger amount of sky. The results from that flight ought to be really worth waiting for.
Could you let us know about the new satelites after COBE which will
study the CMB. What are they going to measure precisely?
Submitted by biswa"AT"media.physics.indiana.edu 11/98
There are two planned satellites. The Microwave Anisotropy Probe (MAP) is a US mission, which is due to launch in November 2000. A European-based satellite, the Planck Surveyor, is scheduled to be launched around 2006.
The satellites have similar science goals: to map the CMB anisotropies over the whole sky as well as possible. This means covering a wide range of frequencies, and having as high an angular resolution as possible. MAP will provide maps which are a huge improvement over the crude resolution and relatively low sensitivity of COBE. Planck aims to be the definitive CMB mission, mapping the sky at all relevant frequencies, and with an angular resolution matched to expectations for the anisotropies. You can think of them as the second generation and third generation CMB satellites, after COBE.
Rather than me saying any more, let me point you to the horses' mouths. Many more details can be found at the web sites for MAP and Planck.
What are the advantages of using interferometry, such as CAT and DASI,
in obtaining data about the CMBR?
Submitted by micky"AT"acon.com.au
Interferometers use correlations between multiple dishes to make maps of the sky. These maps contain information with an angular resolution (visual acuity) which is in principle the same as a telescope with diameter equal to the spacing between dishes. In practice a set of observations with different "baselines" (distances between the dishes) has to be combined in order to build up the full picture, with both large and small scale information fully represented in all directions.
Because of this correlation nature of interferometers, they are naturally taking differences between sets of signals on the sky. Hence they are very good at subtracting out the effects of the atmosphere, as well as effects due to lack of complete stability in the detectors. These kinds of "systematic" effects can be reduced by being very careful in taking and analysing the data from single dish experiments, but certainly this should all be easier with an interferometer.
It is also generally easier to build an interferometer which probes the smallest angular scales. This is because the angles that you probe in the sky are inversely proportional to the length scale of your system. And it's obviously easier to build an interferometer with small dishes 100 metres apart than to build a 100 metre dish.
Over a range of angular scales in which there is lots of current interest (namely from several degrees down to several minutes of arc) the single dish and interferometry approaches are both competitive. Hence there is one prototype interferometric experiment in existence (the Cosmic Anisotropy Telescope) and at least 3 more ambitious experiments being built: the Cosmic Background Interferometer (CBI); the Degree Angular Scale Interferometer (DASI); and the Very Small Array (VSA).
I am interesting in the CMB since my thesis is dealing in a noise processing
method. I believe that the CMB looks like a "noisy" signal in the time domain.
I am interesting in exploring its characteristics.
Submitted by sarafian"AT"inter.net.il 1/99
Interesting question. I'm not entirely sure what it is that would be most useful to you however. The COBE time-series signal was a fairly large set of noisy temperature differences on the sky. This had to be reduced to a set of averaged data, with various systematic effects removed from the data. Then the temperature differences between a huge set of pairs of positions had to be converted into a map of temperatures on the sky. More recent balloon experiments are similarly a set of temperature differences, and information about where the instrument was pointing at each time. Most raw CMB data files will be large - probably larger than you might want to deal with!
In general the "noise" in the data will have non-trivial properties, such as correlations in space and in time. These have to be removed in order to reveal the cosmological signal. Obviously this whole business can get quite tricky, particularly for large data sets. An additional issue for CMB data sets is that generally the time-stream of data has a very low "signal-to-noise ratio", unlike many other kinds of data which you might encounter. It's only when the data are averaged together that the signal can be seen. And even then, the nature of the signal is that sky has "excess variance" compared with the expected noise. This means that what you end up detecting is a set of splotchy patterns. It's reproducible (because it's real), but it isn't a "neat" signal, like a high contrast picture with nice sharp edges. There's a growing literature on ways of analysing signals from CMB experiments. However, much of the stuff used for more conventional signal processing is unfortunately not useful.
Probably you want to choose some simpler kind of data set to look at. But if you really want time-ordered data from a CMB experiment, then I have no doubt that many of the experimental groups would be happy to give you their GB worth of data to play with!
Why doesn't other sources of microwaves interfere with the smoothness of
the CBR? Wouldn't other sources of micowaves and other sources of
radation at other wavelengths that may get shifted into the same
wavelength as CBR make it hard to measure the CBR?
Submitted by deanf"AT"ecluboz.com 6/00
This is a most excellent question!
The answer is, of course, yes. It is crucial in measuring these tiny signals to investigate whether sources other than primordial temperature variations can be contributing. This is done through various means. The best way is to measure the anisotropies at a number of different wavelengths, and then test for whether the wavelength variation is consistent with other known sources of radiation in the local Universe. Gas and dust in our own Galaxy are particularly problematic. This means that it is hard to get decent CMB data near the Galactic plane, but away from the plane it turns out that these local sources of confusion are quite small. And if you make maps at several microwave wavelengths then it is relatively easy to tell them apart.
You're absolutely right that this is a source of concern for CMB experimenters, and they work very hard to check whether they are seeing some faint dust in our Galaxy, for example. But, for the best CMB data-sets (e.g. from COBE or the BOOMERANG maps) there can be no doubt that most of the signal seen is due to genuinely cosmic structure.
I'm currently an undergraduate doing research work in astrophysics and
cosmology. I'm currently trying to convince my
over-seers to allow me to do research with CMB whether on a balloon or from
ground.
I was wondering if you would either be able to lead me in the direction of a
information source that would suit my needs for general economic, logistic,
and instrumentation information?
Submitted by pelcher"AT"hotmail.com 7/00
This sounds very ambitious!
The answer depends on what exactly you had in mind. I can imagine a very instructive and useful undergraduate research project to determine (say) the temperature of the CMB at some particular wavelength. This is far from impossible, since in fact the CMB is a very bright source. I'm not saying it would be easy, since probably it would involve a lot of hard work. But it's probably well within the scope of an undergraduate project, and could well teach you an amazing amount.
However, attempting to put together an experiment to measure the anisotropy in the CMB would be an extremely ambitious project. The temperature differences are very small, and it is very easy to measure things other than variations in the CMB sky.
I suggest that the most useful thing might be for you to pay a visit to the CMB experimental group which is nearest to your home, and ask them for specific ideas. If you tell me which college you are attending, then I can try to put you in touch with someone. Maybe you could even do something to help out part of one of the current CMB experiments?
Good luck!
I was a co-op student
(Electrical Engineering) at BTL in the 1960s, about when the CMB was first
discovered by Penzias et al. There were a lot of jealous comments from the
Murray Hill solid stated physicists to the effect that "... all those guys
did was clean the pigeon s*** off their antenna, and for that they're going
to get a Nobel Prize ..."
Submitted by a.ross"AT"ieee.org 10/00
Thanks for sharing that!
The whole history of the discovery of the CMB is quite fascinating, with several twists and turns. The role of pigeon's in this story is nicely recollected in a section of Marcus Chown's popular book "Afterglow of Creation", called they died for Science!
I am currently researching the CMB in general and have a wide range
of information on the CMB theory and implications. But I am having a
really hard time trying to find information on the experimental
methods used... is there any chance you could direct me to a sutible
web page or journal artile etc..?
Submitted by R.C.Simpson"AT"newcastle.ac.uk 12/00
Every experiment is of course different in several ways, and so you should look at information about a few separate projects. Most of the experimental groups have their own web-page. I have a fairly up-to-date list here. Many of these web-pages contain technical details explaining how the experiments are carried out. I suspect there is more than enough here to keep you going!
Do you know of any books or scientific journals written on the
COBE and MAP missions that I might have access to through my local
library?
Submitted by bjserink"AT"home.com 3/01
There are at least 2 books written by members of the COBE team, with two different points of view. One is by George Smoot and Keay Davidson, called "Wrinkles in Time" published by Avon Books. The other is by John Mather and John Boslough, called "The Very First Light : The True Inside Story of the Scientific Journey Back to the Dawn of the Universe", published by Basic Books. MAP hasn't flown quite yet - but you can bet there will be books eventually!
I notice that every experiment I've read about, from the very first
Penzias/Wilson observation, used a cryocooled detector.
Is the background bright enough that some backyard experimenter could detect
it with today's low-noise electronics at room temperature?
Submitted by fwamsley"AT"wirelesscorp.com 9/01
This is an excellent question!
So excellent in fact that I asked the advice of my colleague Mark Halpern, who is an expert in CMB experiments, having actually built them, rather than just thought about them like me. Here's roughly what he suggested.
You can in fact probably detect the CMB with modern electronic detectors at room temperature. For example you could use a digital satellite receiver. But you probably have to do a couple of crucial things in order to be successful. First of all you want the power from your receiver over a much wider bandwidth than the electronics deals with. So probably you need to get the output as near to the dish as possible, before it has been processed into narrow bands etc. There ought to be low enough noise in such an off-the-shelf system to allow you to detect the CMB provided that you use a broad enough band (GHz if possible).
The second thing you have to do is figure out how to believe you've detected a non-zero constant signal. The easiest way to do this would be to make measurements at a number of different angles from the zenith. Then fit for the expected atmospheric variation (1 over the cosine of the angle) and see if there's a constant offset remaining. That offset is the CMB sky. You'd also have to try to avoid looking at the Galactic plane while you do this, because that will also give a detectable signal. But it should be possible to do this.
I haven't heard of anyone trying this recently with "Radio Shack" type equipment. So I'd be interested to know if you succeed. And if anyone else reading this knows of a useful article I'd also like to know about it.
do they(CMB radiations) get
scattered or reflected continuously from the different living and non
living object of this world? if the answer is yes then my next question
is- is it possible to detect or receive(experimentally) these CMB
radiation scattered or reflected from a particular object?
Submitted by swati_v"AT"isical.ac.in 12/01
The first thing to understand is that the CMB radiation, although it fills the Universe, is a very low energy density. So it is totally swamped by emission from warm material in our Galaxy, from stars, from the Earth's atmosphere, from the ground and from warm bodies (like you or me!).
Although it is certainly possible to detect it, you first have to subtract out the very much stronger local sources of radiation.
The answer to your question about absorption or scattering is that you can easily reflect CMB photons off the right sort of material (what you make a mirror out of for a CMB experiment, for example), but that many materials will just absorb it.
So if you put a CMB detector out in space, and tried to look through the Earth, you might expect to see a big hole there. Except that it's typically hard to make things (even space) colder than the CMB. So in fact the relatively warm Earth would of course appear like an incredibly bright hot-spot in your image. But it would certainly be impossible to observe the actual primordial CMB photons (tracing out the anisotropies, say) through an object like the Earth.
How did Penzias and Wilson know they had 3 degree radiation?
Didn't they just have the one reading at 7.35 cm? That could be in
any black body spectrum I want couldn't it?
Submitted by wrx"AT"mail.cruzio.com 12/01
That's correct. Penzias and Wilson had no way of knowing how close the CMB was to a blackbody. However, their measurements were on the long wavelength side, and there the brightness is easily related to a temperature, which they estimated to be about 3 Kelvin. It was only when measurements of the brightness had been made over a wide range of wavelengths (including both sides of the peak) that it was clear that the spectrum was close to blackbody. And we now know that it's very close of course.
According to te latest MAP data the product of the Hubble parameter and the
age of the universe is approximately 1 instead of 2/3. Please explain.
Submitted by LABELE"AT"aol.com 03/03
If the Universe had always been expanding at the same rate, then the time in the past when everything used to be in the same place is just 1/H0. However, this can only be the case if the Universe is completely empty. Models which contain matter will be slowing down due to the positive attraction of mass, and hence the Hubble parameter will have been larger in the past. Hence the age of the Universe will be a bit smaller than 1/H0. For a Universe with critical density in matter, it turns out that H0t0=2/3. However, the existence of Dark Energy makes things more complicated, because the Universe is now accelerating. It turns out that you get close to H0t0=1, even although the Universe used to be decelerating and now is accelerating. This depends on the precise values of the parameters which describe the model. But for the currently favoured values it turns out to be true that H0t0 is quite close to 1.
Why is microwave radiation used for measurement instead of other
wavelengths like Infrared or Gamma ray?
Can the same measurements be done with a radio receiver?
Submitted by 0nthony"AT"unihedron.com 5/03
The CMB radiation peaks at microwave wavelengths. But it is still measurable at longer (radio) wavelengths and shorter (infrared) wavelengths. However, it's entirely negligible at very short wavelengths like optical or gamma-ray.
Because the best range for observing (around a wavelength of 3mm) lies between the radio and infra-red bands, the measurements are done with a combination of radio techniques and infra-red techniques.
In fact the term "microwave" conventionally refers to the frequency range 300MHz (corresponding to a wavelength of 1m) up to 300GHz (corresponding to 1mm). So the CMB lies at the upper frequency (lower wavelength) end of the microwave region of the electromagnetic spectrum.
How weak is this radiation at
ground level? Is it significantly attenuated by atmosphere? i.e. would it be
much stronger on the orbit?
Submitted by 0nthony"AT"unihedron.com 1/04
You are absolutely right that the atmosphere attenuates microwave radiation. Unfortunately the details depend on the precise frequency that you're interested in, as well as other factors such as the weather conditions, altitude, angle to the zenith etc. A lot of the effect comes from water (and other) spectral lines, and so at some particular frequencies the effects are especially bad. But in some frequency bands (particularly lower frequencies) the effects are very modest. CMB experiments designed to measure the overall brightness (or spectrum) will obviously need to correct for this attentuation. For anisotropy experiments the correction becomes essentially part of the calibration procedure - one needs to know how many Volts in the detector corresponds to a given source brightness, with bright objects of known flux (e.g. planets) used to calibrate.
You can certainly find more information on the web. Perhaps the sort of data you are looking for would be given by people who study remote sensing of the earth from satellites, e.g. here
What is the difference between lenses used in microwave devices e.g.
horn lens antenna and binoculars or telescope lenses?
Submitted by TSM"AT"brightok.net 1/04
This is a topic on which I am far from an expert!
There are lenses used for focussing microwaves. They are formed using materials with appropriate refractive indices, or using a mesh of waveguides for focussing the wavefront. However, I think what you're talking about is an antenna rather than a lens.
Optical telescopes come in 2 basic varieties: refracting or reflecting. Typical small telescopes that you buy in the store will use lenses, and these are called "refracting telescopes". Larger amateur instruments and almost all professional telescopes are of the "reflecting" type, i.e. they use mirrors to focus the light. A microwave telescope is basically of this sort too, with a collecting dish which focusses the microwave light onto the detectors, or perhaps onto a secondary mirror which then directs the light to the detectors. Some microwave telscopes (the original of Penzias and Wilson for example) use a "horn antenna" to direct the microwaves into a waveguide through which they pass to the detector. It's more efficient to collect the radiation in a dish and then pass that to a "horn antenna" or "feed-horn" - so that's what many modern CMB telescopes have, rather than the horn pointing directly at the sky.
Is there a way to hear the CMB, that is to say, is there a specific way to
tune in to it so you know your reading it?
Submitted by blindmellojelly"AT"charter.net 12/04
There are answers to similar questions above on this page.
I assume by "hear" you mean detect the radiation and see evidence that you were detecting it in real time? In principle it isn't too difficult to detect the CMB for yourself, since it's about the brightest thing in the sky at microwave wavelengths. However, I'm not aware of any artcile or web-site describing how to go about building a home-made CMB detector. If anyone has seen such a thing, they should let me know.
Does the CMB show ANY deviation from a true black body, no matter how
small, from the results of recent measurments? I've looked at the available
energy spectra I can lay my hands on, but thought it would be useful to
actually ask someone more intimately involved with CMB than I am.
Submitted by ma"AT"star.ucl.ac.uk 02/05
Right now I'm not aware of any evidence for any deviation from a pure blackbody spectrum. The upper limits are pretty tight, depending on the form of the deviation you have in mind of course. The measurements come from a range of different experiements, dominated by results from the FIRAS instrument on the COBE satellite at the higher frequencies, and with many experiments contributing measurements at lower frequencies (including the ARCADE experiment most recently).
[abridged] one
thing that has been puzzling me for a while is whether the CMB should appear
as uniform as it does (in both spatial distribution and polarisation
distribution) when one takes into account quantum uncertainty that surely
must be encountered at the 'last scattering surface'? The release of
photons from the photon-baryon fluid seems to be too uniform to my way of
thinking if the only process was cooling through expansion?
Submitted by ma"AT"star.ucl.ac.uk 03/05
There are no quantum effects that I'm aware of, happening at the last scattering time, that are even close to being significant for the CMB anisotropies. It may be, of course, that you have something in mind that no one else has thought of - that would be very interesting!
It's also true that in the now conventional inflationary model for the early Universe, all the structure in the Universe comes originally from quantum fluctuations, i.e. the CMB anisotropies, galaxies, and everything else. So at very early times, quantum effects certainly are important.
how do you measure cmbr?
Submitted by bgy3reb"AT"leeds.ac.uk 03/05
If this question means how do I measure the CMB, then the answer is that I don't! I'm a theorists/data analyst, and leave measuring the CMB to people who actually know how to do it!
On a question: Can I see the CMB for myself? - you answer:
- In fact you can! If you tune your TV set between channels, a few percent of
the "snow" that you see on your screen is noise caused by the background of
microwaves.
What proofs? Exact and sensitive devices may show Cosmic Microwave Background.
The TV set cannot be named such device, - assert a repairman (TV sets)
Submitted by nonstop"AT"fort-dks.dp.ua 08/06
This isn't supposed to be "proof" for the existence of the CMB, just a cute idea. In fact modern TV's filter out noise and automatically tune into broadcasting channels, so you can't easily do the experiment!
You do need a very senstive device to measure the CMB anisotropies, since the variations are so minute. But you don't actually need a very sensitive detector to measure the existence of the CMB itself, since it's actually pretty bright at microwave frequencies. The trick is to build a device which is capable of measuring the absolute level of the microwave sky, which isn't as easy as it sounds.
how did Penzias/Wilson remove from their measurements
the radiation from the horn itself or radiation
from the atmosphere ?? Since these bodies are
above absolute zero, they have an emission spectra albeit very low,
from photos I have seen neither the horns nor the
chopper at the mouth of the horn are cooled to liquid helium as was the
detector.
Submitted by jnz9876"AT"yahoo.co.uk 10/06
I really wouldn't claim to be an expert on making absolute measurements of the CMB! And certainly I don't know exactly what Penzias and Wilson did. But I do know that removing all of the other sources of noise is a difficult procedure, and something that Penzias and Wilson took great care over. This is the main reason that they took so long to convince themselves that they were really seeing a cosmic signal. So you are right to wonder about how this is done in practice!
All such experiments are intrinsically "differential", i.e. they measure the difference between two things. This may be the "sky" versus a known "source", or it may be the difference between positions on the sky. By making many such measurements and calibrating things very carefully, it's possible to separate the emission coming from the telescope, from the ground, from the atmosphere, from the plane of the Galaxy and from the distant Universe.
I'm a high school researcher at
Harvard-Westlake School in Los Angeles. I'm intrigued by the continuing
analysis of cmb, and though I realize that an advanced background in
astrophysics is necessary to appreciate many of the recent developments
in the field, I would like to increase my understanding and develop
research in whichever ways possible.
As you study cmb, perhaps you have some suggestions for starting very
basic research into cosmology.
Some ideas I think might be within the realm of possibility for high
schoolers are
-building a homemade radiometer to "see" the background radiation for
myself (or obtaining discarded university equipment to do so)
-measuring the peculiar velocity of our local cluster through the cmb via
analysis of the dipole
-matching up anisotropies in the cmb with observed locations of galaxies
Submitted by gold.adam.07"AT"hwstudents.com 12/06
These are very good ideas, and I wish you luck on your quest to perform research on the Cosmic Microwave Background!
Building a detector of the CMB is in fact fairly simple (although I confess that it might be beyond my own experimental abilities!). The trick is to be able to make an "absolute" measurement. I'm not aware of anything written to describe how one might do this in practice. But if anyone knows of a relevant article or web-site, I'd be very glad to hear about it.
Measuring the dipole starts to become something difficult, since it's about one thousandth the amplitude of the CMB itself. So I suspect that this would be too ambitious a project for the High School level. But don't let me stop you if you're keen!
Something involving analysing existing CMB data is certainly feasible, and probably the easiest of the 3 suggestions. Data from the WMAP satellite are publicly available and easy to download from the internet. The trick is figuring out how to manipulate those data, which can be done using a variety of computer applications. To do this probably requires a fair level of competence on a computer, e.g. the ability to program in some language (or at least write scripts for some image processing application). There are many things which could be done with the data-sets once you know you can download and manipulate them. Correlating with the positions of nearby galaxies or clusters is one simple possibility. Again it's possible that someone has already thought out and written up some projects which might be doable at the High School level - and if so I'd be happy to advertise them here.
My senior design project is to design and build a 20 kg balloon payload to
detect the cosmic background radiation. I've done extensive research into
measurement devices and techniques, but the one thing I'm not sure about is
this: if I don't use cryogenics, will I be able to detect the CMB. I am not
trying to detect anisotropies of the CMB, but I'm just trying to find it and
have enough data to be worth while. If I don't use cryogenics, do I still
need HEMTs to amplify the signal or can I use other means of filtering the
data. Any input you can give would be of great help.
Submitted by raynman4451"AT"att.net 11/07
I have to confess that I am very far from being an expert on how to build CMB experiments!
However, I think there's plenty of literature out there which will be helpful to you for the details. I think you should focus on some of the early CMB papers, since what you are attempting is, in a sense, a historical recreation of the discovery of the CMB.
You don't of course actually need a balloon for this project, since the CMB is pretty easy to measure from the ground at its low frequency end. But if you want to go to higher frequencies (above, say, 20GHz), then you're probably better off at high altitude (unless you're at a very good observing site).
The basic issue here is how you tell that you've detected the CMB! Penzias and Wilson struggled with their measurement of "excess noise temperature", ruling out all possible sources except for the Cosmos. It's easier to make an "absolute" measurement of you have directionality in your detector, since then you can make measurements at a range of zenith angles, and work out whether there's a "floor" to how bright the sky is.
In a way this absolute measurement is a lot trickier than just measuring how bright the Galactic Plane is at some radio wavelength - since that just requires measuring a difference in brightness between positions on the celestial sky. But what you're trying to do (I assume) is to measure the "DC level" of the sky. The best way to do such a measurement is to force it to be differential, e.g. by having a "cold load" in your aparatus, so that you constantly measure the difference between the sky and the internal source - but that will make your aparatus a lot more complex, and require cryogenics.
I hope this has been of some help. But, as I said, you don't have to listen to me, since I've never built anything remotely like a CMB experiment myself!
I am aware that they have planned another mission using Planck to observe the
microwave background... But why is it necessary for the telescope to be so far
away from Earth?
Submitted by r.karzai"AT"utoronto.ca 1/08
There are several reasons to prefer a distant satellite orbit. But probably the most important is the requirement of a very stable thermal environment. You want the satellite to have pretty much the same solar heating all the time, and not to have the Sun, Earth or Moon wandering in front of the telescope on a regular basis. It turns out that an excellent place for fulfilling this requirement is the "L2" Lagrange point of the Sun-Earth system. This is a point outside the Earth's orbit, where the additional gravity of the Earth makes it go round the Sun in exactly 1 year, despite being a little further from the Sun than the Earth. It's not a stable orbit, so spacecraft will wander away if you place them there, but this is on a sufficiently slow timescale that it makes it an ideal spot for space astronomy experiments lasting a few years. Hence WMAP is there, Planck and Herschel will go there, and eventually they will be joined by the successor to HST, which is called JWST.
I have just read your article about the cosmic background radiation, and am
intrigued as to how the cosmic energy of what is this background radiation is
viewable on t.v.
How do these microwaves travel in reverse of an expansion? As I guess I always
thought it was something more local..I.e the sun.
Submitted by Electrodynamic"AT"hotmail.co.uk 07/09
The CMB radiation just fills the Universe. It's everywhere, and so we see it coming from all directions.
Any radio receiver (including a TV) will have "noise" coming from all the unwanted background radio signals. This includes the CMB. It's not really viewable on your TV, but a fraction of the noisy background of any radio signal is due to the CMB.
And the microwaves don't travel in reverse of the expansion. They travel at the speed of light, having left everywhere in the Universe at quite early times. They travel freely through the expanding Universe, losing energy (redshifting) as they do so.
How can the CMB penetrate the ionosphere and earth's atmosphere?. Now we
have satellite orbiting the earth that can detect the CMB but how was it
detected on earth without the satellite
Submitted by rahmaniz68"AT"gmail.com 05/11
The Earth's atmosphere is transparent to most radio waves, and that includes microwaves (which are essentially the shortest wavelength kind of radio waves). If that wasn't true then your cell phone wouldn't work! So you don't need to go to space to observe the long wavelength side of the CMB spectrum.
At the shortest wavelength (highest energy) end of the CMB spectrum, which is at wavelengths of a fraction of a millimetre, the atmosphere is opaque. You can observe at these wavelengths from some of the best mountain-top sites in the world, or from hih altitude balloons, or from satellites.
How signal processing can be useful when dealing with
the CMB?
Submitted by zouaouiyoussef"AT"gmail.com 03/14
CMB anisotropy signals are very very weak. That means that to extract the maximum amount of information from CMB experiments, it's important to use careful statistical methods. These methods are based on ideas from signal processing, linear algebra and Bayesian statistics. If you're really interested you can read much more about the details in the original research papers.
I'm a high-school student looking into the possibility of doing a project
on Cosmic Microwave Background Radiation. This would involve building a
system to pick up CMBR and using this to carry out some analysis of the
radiation. However I am not sure that this is possible and wanted to ask:
a) Is it in any way possible to build a DIY system sensitive enough to
detect the CMB on Earth in your opinion?
b) If you collected a signal, how would you distinguish the CMB radiation
from microwaves from other sources?
Submitted by imiriv2718"AT"gmail.com 11/15
This is a very good question, and I'm impressed that you'd like to try to detect the CMB in a school project!
Unfortunately, I think it may be a little harder than you think. Not impossible of course, but a bit challenging. It should be feasible for you to construct a microwave telescope, from which you can detect different things. An ambitious goal would be to try to detect the Sun and perhaps even map the emission from the Milky Way. However, the CMB is mostly just a constant signal (i.e. the same in all directions), and that's one of the hardest kinds of signal to measure well.
If you're interested in this topic, I suggest you see how far you can get in constructing what would essentially be a small radio telescope. There are certainly descriptions of how to do this available on-line. For example, I found resources here, here and here. But I am sure you can find other descriptions by people who have successfully built something like this for themselves.
Good luck!
What determines the ratio of photons to baryons in the early universe?Submitted by padwick"AT"physics.ubc.ca
What this question is asking is why there are so many more CMB photons than particles of matter (protons and neutrons are sometimes called "baryons") -- the ratio of densities of photons to baryons is about 1 billion. This number is somehow related to particle physics at the highest energies and the "baryogenesis" question.
Presumably early enough in the history of the Universe, all species were in complete equilibrium, meaning essentially equal densities of all particles with mass below the characteristic energy at that time. This would of course involve antiparticles as well as particles, i.e. there would be as many positrons (anti-electrons) as electrons, as many anti-protons as protons etc.
At some point the temperature dropped low enough that when particles annihilated there wasn't enough energy around to recreate the pairs. So particle + antiparticle gave photons. If there was an exact balance then there would be only photons today. But since the Universe is observed to be all matter, with about 1 proton per 109 photons, then there must have been an imbalance between matter and antimatter in the early universe. And so we know that the laws of particle physics at high enough energies must contain non-conservation of baryon number, at the level of 1 part in 109. So when the Universe cooled enough, all the matter and antimatter annihilated, leaving about a billion photons for every proton.
Exactly how this worked is an area of active research, with lots of good ideas, but no clear winner yet. The point is that the photon-to-baryon ration is an observable which tells us directly about properties of particle physics at extremely high energies. It's surprising that the mere observation that there's no anti-matter today, and that there are many more photons than baryons, is such a non-trivial observation!
Why are there so many photons in the universe?
Submitted by francis4"AT"tcnj.edu 11/98
A very good question, and I must resist the temptation to answer "why not"!
As I mentioned in reply to the last question (and others earlier), particle-antiparticle pairs can be created out of pure energy (i.e. photons), and then annihilate again to produce photons. This happens if the average energy of the plasma is high enough that it's more than the rest mass of whatever particles you're thinking of creating. Once the energy drops below that level then you favour annihilation over creation, and you end up with a bunch of photons, and not many particles. That's what happens as the Universe expands and cools.
If the Universe was born with an exactly equal number of particles and antiparticles (which is the simplest assumption), then mostly they'd have annihilated, and you'd eventually have almost nothing left except radiation. In fact in an expanding Universe you don't get quite zero, since you reach a point where the density of particles and antiparticles is so low that they can't find each other, but in any case the trace amount left is almost entirely negligible. There are currently about a billion CMB photons for every particle (more technically every baryon, i.e. proton or neutron) in an average part of the Universe, whereas a particle-antiparticle symmetric Universe would have a ratio which is many orders of magnitude higher. So the real question, given the present density of particles is "why are there so few photons in the Universe?"
The reason is, that through some detail of particle physics, the early Universe preferred particles over antiparticles, ever so slightly. So when most of the anti-baryons annihilated, there were still some baryons left over. Given the ratio of photons to baryons of about a billion, it would appear that some high energy physics process favours baryons over antibaryons at the level of about one part in a billion. Exactly how that happened is an area of ongoing research in a field called "baryogenesis" or "baryosynthesis". The fact that the CMB gives a clue to some mysterious high energy physics process is a good example of why some people refer to the early Universe as the ultimate particle accelerator!
At what actual transition temperature would hydrogen gas emerge from an
electron-proton plasma?
Submitted by debouche"AT"kings.edu 1/00
The early Universe was much hotter and denser. At some point the average hydrogen atom must have been ionized by the hot radiation bath. This can be calculated quite precisely, knowing the current temperature of the CMB, together with the current density of matter and the expansion rate. The answer turns out to be a temperature of around 4000 Kelvin. The photons last interact with the matter at the slightly lower temperature (due to the small amount of plasma still remaining by then) of around 3000 Kelvin. This corresponds to a redshift of about 1000, or a time of about 300,000 years after the Big Bang.
If you want to know all the gory details of the process by which the Universe evolved from a plasma to being neutral (usually referred to as "recombination") then see my paper at this archive (but be warned it is long and boring!).
What would happen to the Earth if the Sun instantaneously became a black
hole? Would the Earth get sucked into the black hole like a vacuum cleaner?
It is only very close to a black hole that things get strange. At large distances gravity behaves just the same way as it does for any other sort of massive object. So if the Sun suddenly became a black hole nothing very special would happen. The earth would carry on orbiting the Sun exactly as before, and even the orbits of Venus and Mercury would be unaffected. Of course the Sun would stop being luminous, which would have somewhat drastic consequences for all life on earth!
In fact the Sun will not turn into a black hole. Only very high mass stars (greater than about 8 times the mass of the Sun) are likely to become black holes when they reach the ends of their lives. When a star like the Sun runs out of fuel (in about 5 billion years) it becomes a red giant, throws off some of its outer layers, and then fades into obscurity as a white dwarf.
I understand how the 0
can be determined by the angular
scale of first Doppler peak. What I don't immediately see is how we know the
physical size of the horizon at decoupling, which is needed to figure
out how the geodesics curve.
Submitted by borys"AT"physics.ubc.ca
The point is that the relevant physical scale at the epoch of last scattering,
is almost model-independent. This scale is the "sound horizon", meaning the
distance that a sound wave can have travelled in the age of the Universe.
It is this scale which is imprinted on the anisotropy power spectrum, through
the physics of the gravity-driven acoustic oscillations in the early
Universe. If the speed of sound is denoted by cs and the
age of the Universe by t, then the sound-horizon is just
cst. It turns out that the sound speed during this time is
close to the sound speed for an ideal gas of relativistic particles, which
is the speed of light divided by 3 (take my word for
this for now!). The age of the Universe at the time of last scattering is
also relatively model-independent, and hence the sound-horizon is pretty much
a fixed physical quantity.
The angle that this length subtends on the sky will depend on how curved space-time is. It will look like a larger angle in a universe which is positively curved, so that light rays appear to converge, and a smaller angle in a negatively curved universe (i.e. an "open" universe, with less than the required density for closure). The main effect on this angle is this curvature of the Universe. Other effects (e.g. the ratio of normal matter to dark matter, whether there is a cosmological constant etc) are also measurable in principle, but don't make as noticeable a difference.
I tend to think of a cosmological constant as repulsive gravity. If
matter < 0.3
and we want to close the universe, it seems to me adding
a
would just make things WORSE!
(0 =
matter +
= 1
as predicted by inflation).
What point am I missing?Submitted by borys"AT"physics.ubc.ca
Of course the sign is just a convention. But you are right that the "+" sign corresponds to an effectively repulsive force, and at the same time gives a positive contribution to the overall density of the Universe.
The reason for this is really down to General Relativity, and I think it
would be a lie to claim that there's a simple non-GR explanation. Einstein's
field equations can be used to describe the whole Universe, and the solutions
still work you can if you add an extra constant
(), which can be
interpretted as the energy density in the vacuum. In cosmology the common
form of Einstein equations are normally referred to as the Friedmann equations,
and they describe how the scale of the Universe changes with time depending on
the contents of the Universe. As well as the normal matter density parameter
(),
you can also consider models with an additional
term.
If you write down the Friedmann equations with just a
term, and it has
the usual positive sign, then exponential expansion results. This is just
what happens during an inflationary epoch in the early Universe, when
the expansion was driven by a large energy density in empty space (which
appeared for some reason that particle physicists will understand one day!).
So inflation is just a -dominated universe, and you can think of this
extra energy of empty space corresponding to a "repulsive gravity". This
repulsive term is what you get if you have
with the usual positive sign.
Inflationary models generally predict that we should have (in appropriate
units) + = 1.
This corresponds to flat, rather than curved,
space for our Universe. The Universe is expanding, but the space within it
has a flat rather than curved geometry.
Observations today suggest that we may live in a Universe with say
=0.3.
And many people prefer a model which is still flat, so that
the contribution to the density from a cosmological constant term is about
0.7. The Universe you get is closed in the sense that the curvature is flat.
But it's a Universe which is starting to get dominated by the
term,
i.e. if we live in such a Universe then we're just starting to inflate again!
So if this is really our Universe, then it's flat space, but will expand
forever, so that it's "open" in that sense.
Does the universe have some net angular momentum (i.e. is it rotating
as a whole)? If this were so, would it be observable somehow?
Submitted by chunter"AT"unixg.ubc.ca
Of course it's possible that the whole Universe is rotating (although let's not get into the issue of what it's rotating relative to!). But there are quite strict limits on how fast this rotation could be.
Like other things to do with the large-scale properties of the Universe, the best constraints come from the CMB. A rotating Universe would leave some recognizable pattern on the microwave sky - which we don't see. The general limit is about the size of the detected CMB fluctuations in dimensionless units. In essence this means that the rotational frequency has to be less than about a 100,000th of the expansion rate, or equivalently the rotation period has to be more than about 100,000 times the age of the Universe. That's a very slow rotation!
For specific models the limits are tighter still. The simplest rotating Universe is one which is entirely uniform on the largest scales, except for having rotation about some axis. It turns out that such a universe would have a spiral pattern on its microwave sky! The absence of such a pattern, even at a very faint level, in the data from the COBE satellite, allows very strict limits to be placed, which are as much as 10,000 times stronger. Such a universe (technically called a Bianchi VIIh cosmology) can only have rotated by a tiny fraction of a second of arc in the whole age of the Universe.
So the simple answer to your question is that we now know with a fair degree of certainty that our Universe isn't rotating.
I have two questions for you. Firstly, how do astronomers date the universe,
what evidence do they have for saying a galaxy is 3 billion or 10 billion years
old? Secondly how can one distinguish, say, a ScdV galaxy from a SBabII
galaxy - what are the criteria to look for?
Submitted by nigerian1"AT"hotmail.com
I am not really an expert on either of these two topics, but let me give you brief answers.
For your first question, you figure out how old the Universe might be by trying to estimate the age of the oldest objects you can reliably find ages for. Locally we can use isotope ratios (radiological dating) to estimate that the solar system is around 4.6 billion years old. And then similar techniques can be used to date material throughout the disk of our whole Galaxy to be at least perhaps 10 billion. The oldest stars we know about appear to be those in some of the globular clusters in the outer regions of our Galaxy. The ages of globular clusters (agglomerations of thousands or even millions of stars) can be estimated by looking at which stars have already began to run out of nuclear fuel, and calibrating this using the properties of nearby stars and the physics of stellar evolution. The oldest globular clusters turn out to be perhaps 12 billion years, with some estimates being even higher. The end result is that we believe our Universe to be older than maybe 12 billion years, while there is no evidence that it needs to be much older than that.
Galaxy classification is just a matter of recognizing features in the make-up of a galaxy: shape, strength of spiral arms, presence of a central bar, general size, etc. Of course this is just pigeon-holing, and is only really useful if the classification scheme helps you understand how galaxies "work", or even better how they might have formed. This might be similar to observing different cars for instance - if you wanted to know how cars work, then certain properties might be useful (e.g. what sort of fuel they use, etc.), while other properties (e.g. recognizing the make of car) might not help with any fundamental understanding at all. Having said that, the main way of classifying galaxies has been useful because it appears to distinguish some fundamentally different sorts of object. Certainly ellipticals appear to be very different from spirals, and dwarf galaxies are different from giant galaxies.
For more details on this I suggest you search around with your favourite search engine on something like "galaxy classification". And for your first question look for something like "globular cluster ages". I found a whole bunch of useful information when I tried this myself, - and much more detail than I could give here.
I work on the Oxford English Dictionary in the U.K., where I define new
words. Today I am working on "overdensity" but unfortunately I'm not
exactly sure what it means!
I read your page which said "a region with more matter than the
average", but I wondered if
there was any more to it than that. e.g. do galaxies form from
overdensities?
Submitted by elenz"AT"oup.co.uk
It's interesting to get this query from you! Overdensity is one of the words I use fairly frequently, but which I have to keep in my personal spell-check dictionary!
Let me explain the picture here, so you have a clearer sense of the word. Standard models of the early universe have everything being very smooth, but with regions which are ever so slightly denser than average and regions which are ever so slightly less dense than average. Gravity acts to enhance the higher density regions, so they get more and more dense and eventually form into galaxies etc., with lower than average densities in-between.
This is such a fundamental part of the modern picture of structure formation in the Universe, and discussed so frequently in the scientific literature, that words are needed to describe these regions. Hence an "overdensity" is a region which contains more density than the average, with "underdensity" being a region with less density than the average (and here by "density" I mean the usual mass per unit volume). Since overdensities are more important than underdensities (in the sense that galaxies etc. from from them, rather than spaces between galaxies), then "overdensity" has also been appearing quite frequently in the popular science literature.
Where these overdensities come from in the first place is of course a matter of active research. And exactly whether every overdense region ends up forming a galaxy is also probably complicated. But certainly there had to be overdensities in the distant past, otherwise we wouldn't be here! And today, our galaxy is very much an overdensity, as is the Local Group, all clusters of galaxies, and on larger scales super-clusters are still overdense.
I have just been reading an article in Sept 98 Scientific American about the
QMAP balloon results. It states that the results confirm that the universe
is "flat".
My Question is does a flat geometry imply an expanding but open universe (ie
expanding but at an ever slowing rate) or is the geometry independent of the
rate of expansion?
Submitted by leadbeaters"AT"email.msn.com 9/98
"Flat" does indeed refer to the geometry of space. It means the same
geometry that you (and Mr. Euclid) are used to thinking about. The angles
in a triangle add up to 180o, the area of the surface of a sphere
is 4r2, etc. However, it's not
exactly the same as Euclidean space, since it's expanding!
We know the Universe is expanding because more and more distant galaxies
have higher and higher redshifts. This expansion is an empirical fact which
is independent of the geometry of space (whether it's "flat", "spherical"
or "hyperbolic"). "Flat" means that there is no curvature of space, while
"spherical" means positive curvature (like the surface of a sphere, but in
one extra dimension) and "hyperbolic" means negative curvature (like the
surface of a saddle, but in one extra dimension).
Whether the Universe will expand forever is a related, but different question. The answer depends on what sort of matter dominates the density of the Universe. Universes with the hyperbolic geometry are usually referred to as "open", since they have both infinite volume and will expand forever. Universes with the spherical geometry are referred to as "closed", since they have both finite volume and will recollapse. A flat geometry universe, if dominated by regular matter will expand more and more slowly, but never quite stop expanding and recollapse. However, if there is some contribution from the energy density of the vacuum (sometimes called a "cosmological constant"), as many cosmologists currently believe, then the overall geometry may be flat, but the repulsive effect of this weird form of matter will cause the Universe to expand faster and faster rather than slow down. It's also possible, for example, to make closed universes which expand forever - all you need is the right mix of exotic matter!
The answer to your question then is that it depends! But the current best-guess cosmological model (which doesn't of course mean it's right) has flat geometry, with a lot of common-or-garden dark matter, but an even bigger contribution from the cosmological constant, causing the Universe to be on the verge of expanding more and more rapidly forever. The best evidence for flat geometry comes in fact from the power spectrum of CMB anisotropies, as described in the answers to many questions on this page!
When we say that the universe is expanding, do we mean that space is
expanding? If so, then
a meter stick will also expand and therefore relativistically the
universe will always remain the same size to an observer
inside the universe.
Submitted by DAUISE"AT"aol.com 6/99
There are answers to a couple of similar questions near the top of this page. But this is a little different, so let me try to explain.
Things which are self-gravitating are not expanding (e.g. galaxies, you and me, meter sticks, etc.). The blob of stuff that formed a galaxy used to be expanding, but a little slower than the average, then eventually it stopped expanding and started to collapse, then complicated physics took over (gas and radiation processes, electromagnetic forces, etc.). Once a galaxy has "formed" it no longer cares about whether it's in an expanding Universe or not.
So it's much better to think about the space expanding between galaxies. Objects like meter sticks, and anything else within a galaxy are so much more dense than the average parts of space, that they are unaffected by the expansion of the Universe as a whole. This means that you can in principle measure the expanding space between galaxies by using a common or garden meter stick (I wouldn't recommend trying it though, since I'm afraid that the average human lifespan isn't well-matched to the task!).
Could it be even close to accurate to say that the universe
could be thought of as 15 billion years old for us and six-days old from
the vantage point of "someone" looking from the other side of the
big bang?
Submitted by Plasticplate-eng"AT"worldnet.att.net 10/99
I try to avoid talking about religion here, for fear of offending people. So let me try to answer from the purely cosmological point of view.
Basically, I don't understand what is being stated. The implication is that there is time dilation involved, but that makes little sense (there are big differences between an expanding Universe and the physics of special relativity). If we could see something happen at a redshift of around 1012, then a 6 day long event would appear to us to be stretched out by that factor of a thousand billion and hence be around 15 billion years - but there's no way of observing anything happening at that distant time, which isn't a particularly special epoch. And even if there was, then an observer at that epoch wouldn't be seeing this time dilation. So I can't figure out what is meant here!
Moreover, there is no such thing as "the other side of the Big Bang", since the whole point of the model is that you can extrapolate back arbitrarily close to t=0, when time itself (somehow!) began. But certainly there was a point in the evolution of the Universe when the age was 6 days. However that was long after (speaking relatively of course!) the rather well understood era of synthesis of the light elements. And at that time the light travel distance is only about 6 light days, so there's no way that you could affect things further apart than 6 light days - or in other words the causal distance was 6 light days, which is pretty small (by astronomical standards anyway!). You might argue that it's possibile to break causality and affect the whole Universe. But if you can break causality then you can do anything you like, whenever you like. Or even before!
Do we have an absolute velocity in the universe?
Submitted by mb10117120"AT"isbank.com.tr 2/00
Sort of!
Our motion through the sea of CMB photons shows up as a "dipole" pattern on the sky, with one side of the sky having a redshift (and so appearing a little cooler than average) and the other side having a blueshift (and so appearing a little warmer than average). There is obviously a frame in which we would not observe a CMB dipole at all, and in a sense this defines an "aboloute rest frame" for the Universe.
This seems to worry some people, since Einstein (and all relativists since then) have taught that there is no such thing as an absolute reference frame. But in fact you have to listen a little more carefully to what is stated. The statement of the principle of relativity is that there are no special frames for the performing of any physics experiment. In other words, the laws of physics are expected to be the same in all frames. The fact that one frame has a different observed CMB dipole than another frame is really inconsequential - the performance of any physics experiment (other than merely trying to measure the dipole!) would be exactly the same in all the frames.
So yes, there is in a sense an absolute rest frame. And through observation of the CMB dipole we can measure our velocity with respect to that frame.
I'm hoping you could help me find where or who I might communicate with to
get actual data from experiments concerning how the fine structure constant
varies with energy...
Submitted by skelley"AT"fc.fcps.k12.va.us 2/00
This is an area in which I should make it clear I am not an expert!
Certainly there are some data, at least at relatively low energies (by early Universe standards at least). There are some indications that the strong interaction coupling decreases at high energies, to reach that of the electro-weak forces at some very large energy (more than 10 orders of magnitude higher than are probed in today's biggest particle accelerators). This is the strongest empirical reason to believe in the idea of Grand Unification of the forces at extremely high energies, which must have described the Universe at extremely early times.
If you want more detailed information about particle physics, then I suggest you start by looking at material and resources on the web-page of the Particle Data Group.
Is it a possibility that the universe is closed spatially and open
temporally? (i.e. the universe has a finite mass, but will expand forever.)
Submitted by zylon"AT"netzero.net 02/00
This is certainly possible. I might say that it's even my favourite model for the Universe! That's not so much for empirical or philosophical reasons, but just because it seems to me to be more amusing!
Although I've explained similar things before, let me do so again.
There is a certain "critical density" for the Universe, which
is determined by how fast the Universe is expanding. Specifically we
can write
critical=3
H02/(8 G), where
H0 is the Hubble constant, or expansion rate of the Universe.
It 's conventional to define a new parameter
as the average density of the Universe in units of this critical density, i.e.
= / critical.
The spatially and temporal desciption of the Universe then depends on the
values of , interpretted in two slightly different
ways.
Whether the Universe will expand forever or not, is a balance between kinetic
and potential energies. If the Universe is expanding fast enough compared to
all the normal gravitating matter within the Universe, then it will expand
forever. If there is enough gravitating matter to halt the collapse, then
eventually the Universe will re-collapse. This is determined by whether
matter > 1.
Whether the Universe is spatially closed or not depends on the overall
curvature of space. This in turn depends on the total mass-energy
density of the Universe. This can include exotic forms of energy, like the
energy density of empty space, which there is some reason to believe might
be greater than zero (otherwise known as a postitive cosmological constant).
In otherwords the Universe can be spatially closed, i.e. have finite
volume, if total > 1.
In fact with a positive cosmological constant, or other exotic forms of matter
which behave similarly, the future Universe eventually becomes dominated by
this exotic "dark energy" and can in principle expand forever (even if
matter > 1!).
Cuurently favoured cosmological models have
matter around 0.3-0.4 and
total close to 1 (derived from the
macth to the characteristic angular scale in CMB anisotropies),
with the balance made
up in some form of dark energy. It is certainly possible to have a
Universe where the dark energy slightly overdoes it, and the Universe is
spatially closed but will still expand forever.
What is a black hole made of inside? ...
is a black hole simply full of photons? ...(abridged)
Submitted by jeu198"AT"soton.ac.uk 3/00
Although I'm not an expert in this area, I've answered a few questions on black holes before. So let me give a short reply and then point to a better source of black hole information.
The answer is that black holes are made of whatever collapsed to create the black hole. Exactly what is going on inside the event horizon right now may depend on how long ago stuff fell in, and what form that matter had. It might all be in a singularity at the hole's centre, or it might be more complicated than that. Such speculation is moot however, since you can't tell anything about what's going on from outside the event horizon anyway!
For more answers to common questions about black holes see the Black Hole FAQ pages by Ted Bunn and by Robert Nemiroff.
Could you explain what is the requirement for ANTIMATTER in the structure of
the universe?
Submitted by rgonzalez"AT"nwic.edu 4/00
The Universe today appears to have essentially no anti-matter. You can make anti-particles in accelerators of sufficiently high energy, but they tend to annihilate again with particles pretty quickly. There's also a small fraction of anti-particles in cosmic rays that are raining down on the Earth - these are consistent with the idea that high energy particles smash into heavy nuclei in the interstellar medium, making some anti-particles as well as other nuclear debris. So we know that there are some anti-particles around, but in insignificant amounts.
There has long been speculation (particularly in the pages of science fiction more than in physics journals!) that there may be anti-planets or anti-galaxies in the Universe. In fact the gas that exists in galaxies and even between galaxies would annihilate with any anti-galaxies that existed. And so if there were anti-objects on astronomical scales, then the sky would be glowing with the gamma rays created during the annihilation. The lack of such a gamma-ray signature makes it pretty certain that there's little if any anti-matter in the Universe.
This leads to the obvious question of how the Universe got to be so asymmetric with respect to matter and anti-matter. It's easy to form matter/anti-matter particle pairs from pure energy, but it's essentially always done in equal amounts. Nevertheless, since the Universe is now dominated by matter, then for some reason the physics of the early universe must have preferred matter over anti-matter. This is known as baryosynthesis, and is related to the properties of particles at very high energies, including what is called CP violation (that particles are preferred over anti-particles, by very small amounts in accelerator experiments). There are many ideas for models which carry out adequate baryosynthesis, but no obvious winners yet.
Nevertheless, it's interesting to know that the mere fact that there's not much anti-matter around potentially tells us something profound about high energy particle physics!
Is it really correct to say the universe was smaller at Big Bang time?
Doesn't size imply boundaries?
Submitted by eng"AT"computron-corp.com 4/00
You are entirely correct! It's wrong to say that the Universe was smaller in the past (whether near the time of the Big Bang or any other time).
In an expanding Universe what is meant is that the distances between observers in the Universe is getting larger with time. In a sense this means that the Universe is getting bigger - but if the Universe is truly infinite in size, then in the past it was still infinite, only it was smaller! Infinity can be a tricky concept. This is particularly true if the Universe began with a Big Bang singularity, in which all of infinite space started in a single point! If you know of a good way to picture that, then let me know!
Do you think there is a cause and effect relation between light speed and the
radial space expansion speed of the universe? They appear to be about the
same value.
Submitted by LABELE"AT"aol.com 4/00
I have to confess to not entirely understanding this question, but I'll have a go at answering it anyway!
The speed of light is (as far as we know) a fixed physical constant. The expansion of the Universe is firstly an empirical fact (discovered in the 1920s from the Doppler shifts of galaxy spectra), and secondly is understood through simple models of the Universe (in fact static models are unstable in General Relativity). The rate of expansion is measured as a speed per unit distance. So it has the dimensions of an inverse time. Speed has the dimensions of length divided by time. And so these two quantities cannot be directly compared, since they are entirely different things.
If you interpret the expansion of the Universe as a speed of recession for two given objects, then that speed depends on how far apart the objects are. For objects near the edge of the observable Universe, the speed of recession approaches the speed of light. This is entirely a consequence of what is meant by the "observable Universe". It is really a definition, since something which is so far away from us that it is effectively moving away faster than the speed of light is unobservable!
In many papers the equation of state for the
dark energy is written as w= pressure/density.
Then it is stated that pressure is proprtional to R ^(-n)
where n=3(1+w). Is there a simple way to derive this?
Submitted by shantanu"AT"bu.edu 4/00
Yes there is.
I teach a historical geology class in which I give a lecture on the
Big Bang. My students are often bothered by some of the issues raised in
your "the Universe can't have an edge" answer ... Is the problem that we're
using "universe" in two senses?
Submitted by rlsbk"AT"gly.uga.edu 5/00
I think you're right that there may be a problem with some people using "Universe" in two senses. But personally I try to stick to one use! This is partly why I like to capitalize the word Universe - to emphasize that I mean the entirety of stuff. In other words, one shouldn't think of the Universe as being a collection of things embedded in some larger object, for then that larger object should really be the thing that you label "Universe".
So first of all you should erase any ideas that you can talk about the Universe being "in" something else! This may help clear up the conceptual misunderstanding.
Secondly, the other problem people can have is with a mental image of the Universe expanding outwards. This obviously has no meaning unless there's something the Universe is in, and so we're back to the first problem. To solve this, many cosmologists try to avoid using the word "explosion" to describe the Big Bang. "Explosion" (as indeed the inappropriate term Big Bang itself) conjures up an image of something sitting there localised in space, which then explodes outwards.
Instead think of the Big Bang as being the model in which the Universe is getting less dense and cooler with time, and which can be extrapolated backwards to arbitrarily early times (with t=0 perhaps excluded). Expansion of space should be thought of as the distance between objects getting larger, rather than the volume of space growing as it expands into something.
And always remember that this is hard stuff to get your mind around!
If red shift is a sign that the universe is expanding, why is everything
outside our super-cluster moving away from us? Doesn't this mean we are now
the center of the universe again?
Submitted by DLZC"AT"aol.com 5/00
Objects aren't generally expanding relative to their neighbours, because the local force of gravity dominates compared with the expansion. So you're not expanding, the Earth isn't expanding, the Milky Way Galaxy isn't expanding, etc. The Local Group of galaxies are whizzing around in each others' gravitational pull. And this is largely true for the whole Local Supercluster too. It's only on larger scales that everything is moving apart.
As to the question of whether we are at the centre, consider this.
It isn't obvious until you've worked it out for yourself, but in a uniformly
expanding medium everything is moving away from everything else.
To convince yourself of this you can draw dots on a piece of paper, then
photocopy to a bigger scale (say a factor of 2). That will stretch all
distances by the same factor. Now pick a dot in the first picture and
measure the change in distance for a bunch of the other dots. You'll find
that something that was 1cm away got 1cm further away, something that was
2cm away got 2cm further, something that was 3cm away got 3cm further, etc.
This is precisely the Hubble expansion law: change in distance in a certain
interval of time (otherwise known as speed!) is proportional to distance.
The trick is now to choose another dot and repeat the exercise. You'll
find that exactly the same thing is true. In other words if the Universe
is undergoing uniform expansion, then every observer sees distant things
expanding away according to Hubble's
Speed Distance law.
So in a sense we are at the centre of the Universe, but then so is everyone else!
If there were a big bang, how fast would the stuff have to travel to get out
of the initial singularity?
Submitted by DLZC"AT"aol.com 5/00
Firstly it's by no means certain that there was a singularity. That's just the simplest concept for the beginning. But there are plenty of ideas for more complicated things, which are even harder to picture!
Secondly, if indeed there was a singularity, then it would contain the whole of the Universe. So, by definition, there would be no getting out of it, because that would mean leaving the Universe. The whole Universe would be contained in that single point - it would just stop being a singularity when it started to expand!
If the distance between Galaxies is smoothly expanding, will there some
point in the future where we would not be able see any other Galaxy except
our own (assuming that we survive as a race and the Sun doesn't burn out
first)?
This is true for distant galaxies. But not for objects which are "gravitationally bound" (i.e. not flying apart relative to each other in the expanding Universe). The Local Group of galaxies, for example, is being pulled around by the mutual gravitational forces of all the members. That region of the Universe is expanding away from distant regions, but is not itself expanding. In fact the Milky Way galaxy is currently moving towards our nearest neighbouring big galaxy, Andromeda. We are also bound to many other galaxies within the Local Supercluster. And so we should expect at least those objects to stay in our skies for a very very long time!
Are there any particular text books you'd recommend for the physics required to
understand cosmology more fully?
Submitted by gazic_miles"AT"si.com 6/00
Perhaps the best up-to-date textbook for someone with some physics background to understand modern cosmology is John Peacock's Cosmological Physics, which is published by Cambridge University Press, and a section of which is available here. I probably wouldn't recommend this to anyone who has never taken a university level Physics course, however! For a less equation-laden introduction I tend to recommend one of the two general books by Martin Rees - Before the Beginning: Our Universe and Others and Just Six Numbers, which are available at the usual on-line book sources.
Since both of these gentlemen were once my teachers, then my opinion may be biased (but I think I've been fortunate to have some excellent teachers!).
It seems appealing to think of the universe as a
giant black hole. (You can't leave either the universe
or a black hole once you enter it) Is this point of view
consistent with observation?
Submitted by John.Campbell"AT"siinet.trw.com 6/00
General Relativity seems to be a good theory for describing gravity at all scales and strengths which we have experimentally probed. That theory has a set of equations (known as Enistein's Field Equations) which allow you to relate the distribution of matter and energy to the curvature of space, for any particular arrangement. One set of solutions to those equations involves considering a point mass in an otherwise empty and static Universe. This solution (technically called the Schwarzschild metic) is the approximate situation which describes black holes in the Universe. There is a "horizon" separating the inside of the hole from the outside, so that once you fall in you can't communicate again with the outside.
There is an entirely different set of solutions to Einstein's equations (technically called the Friedmann-Robertson-Walker metric) which describe the curvature of the whole of space for universes which are the same density at every point (homogeneous) and have no preferred directions (isotropic). These are believed to be good models for describing the structure of the entire Universe in which we live. Much of current cosmological research is directed towards figuring out precisely which one of this set of models best describes our Universe.
The answer to your question is that the description of a black hole and the description of the entire Universe are two very different things. In the cosmological solutions there are typically no horizons (although in principle you could contrive for there to be one if you really wanted), and so in that sense we don't live in a black hole. Moreover the Universe is expanding, and, as far as we know, infinite in extent. On the other hand the black hole solution describes a locally very curved region, embedded in a space which is flat at distances sufficiently far from the black hole. And this is really a very different picture.
Modern cosmology is based on the Cosmological Principle which states that
the whole universe is exactly like the locus of man.
Without postulating this principle the observations cannot be interpreted
as cosmological observations... [abridged]
Submitted by zeynel"AT"axiom-one.net 8/00
This is a good point - it is important to keep in the back of one's mind that scientific inferences are always based on a set of assumptions and that there's an additional difficulty in cosmology because we only have one Universe to observe.
The Cosmological Principle is the name given to the idea that we don't occupy a special place in the Universe. This is generally assumed when considering various observations that we make. However, like other assumptions in Science, it is testable. We could discover that in fact we are in a special place, and that the Universe looks very different when viewed by observers at different locations. Then we would have to give up the Cosmological Principle and replace it with something else. However, as far as we can tell the Universe is pretty much the same everywhere - on sufficiently large scales at any rate.
We have mapped out the distribution of galaxies around our own Milky Way galaxy, and there is nothing particularly special about where we reside. We live in the Local Group, which is a pretty wimpy bunch of galaxies. This lies somewhere out towards the edge of the Local Supercluster, which is one of a few tens of similar large scale objects spread throughout the obervable Universe. On still larger scales the Universe is quite homogeneous, with no indication that there are any particularly special directions out there. Failing any good evidence to the contrary, the best approach is to assume the simplest thing, which is that we occupy a perfectly average place.
There are other assumptions we often forget we make, which are also testable in principle. One of them is that the laws of physics are the same everywhere in the Universe. It would be possible to find that this is not the case - however, there is no such evidence at the present time, and so again it is simplest to adopt the working assumption that you can apply the same physical laws everywhere. A last assumption we make is that the Universe is understandable at all! Whether that turns out to be true remains to be seen. But it is quite astounding that Human beings, which encrust this small rock called Earth, have the ability to construct even the sketchiest of models for the whole Universe!
If the observable universe IS "closed", it's probably NOT a Friedmann closure
(not enough density). There is, however, another way to get closure - by
assuming Riemannian space, first suggested about 150 years ago and was the
basis for the first "modern" model of the universe (Einstein's static
hypersphere, proposed in about 1917). [abridged]
Submitted by feltzmike"AT"netscape.net 9/00
This isn't exactly a question, but let me comment anyway!
The connection between Riemannian geometry and the curvature of the Universe is certainly a good one - it was in fact one of the things on Einstein's mind when he came up with General Relativity. The Friedmann models are solutions to Einstein's field equations for uniform and isotropic universes. So Friedmann models are not only consistent with Riemannian geoemtry, they are entirely based on Riemann's ideas!
The only extra ingredient in the Friedmann models is the dynamics, i.e. that the evolution of the Universe is related to its contents. In our particular case we live in an expanding universe, and the rate of expansion depends on the forces due to matter, radiation, dark energy etc. that fill the Universe. So Friedmann models are simply expanding Riemannian geometries.
It now appears that our Universe is close to flat (although expanding). Whether it is a little bit "open" or "closed", in the Riemannian sense, is still to be established though.
I have found
several websites that simply say that a value of Hubbles Constant equal to
x yields and age of the universe of y but they never show how the age is
found from Hubbles constant or how Hubbles constant is even found!
Submitted by jwinsor"AT"kelvin.physics.mun.ca 10/00
The Hubble expansion law is v=H0d, where "v" is the recession velocity of a galaxy, "d" is its distance, and "H0" is Hubble's constant. The way to find ths constant is to measure the speed and distance for a bunch of galaxies and fit the best value of H0.
Measuring speeds is the easy part, since the spectra of galaxies are redshifted, and measuring the shift in the spectral lines gives the speed directly. Estimating distances is the hard part. A range of different techniques is used, mainly involving comparing properties of distant objects with nearby objects whose distances have already been estimated with other methods. Generally astronomers are ecstatic if they get distances accurate to say 20%!
The end result is that the Hubble constant has its order of magnitude very well determined, but its precise value still elludes us. Normally it is quoted in the units of km/s per Mpc (Mega parsec, roughly equal to 3 × 1022 metres), because velocities are usually measured in km/s and cosmological distances in Mpc. The values found are typically in the range 60-80 km/s/Mpc.
As to the age of the Universe, that's easy in principle, but in detail depends on the precise model. The easy part is to imagine running the Universe backwards in time. If it had been expanding at a constant rate, then all points in the Universe would come together a time 1/H0 ago. So this is the estimate of the age of the Universe (if you think about the units of H0 you'll notice that it's really just 1/Time in peculiar units). The complicated part is that the Universe hasn't been expanding at a constant rate, and so the true age depends on the past history. Typically the Universe gets decelerated by the mass within it, and so the 1/H0 estimate of the age is too high. But in models with so-called Dark Energy (also known as the cosmological constant or vacuum energy), the Universe has recently started to accelerate, and then 1/H0 is closer to the correct age.
Do you know where I can find an estimate of the total mass of the
universe?Submitted by cmcdonald"AT"regenstrief.org 10/00
From observations of the Universe it is possible to determine the average
density. In other words the mass per unit volume (or the mass-energy
equivalent per unit volume). Currently the mass-energy census of
the Universe identifies at least 5 separate components: ordinary matter
(baryons); massive neutrinos (a known, but ellusive particle, which may have
a small mass); cold dark matter (some as yet unidentified particle); photons
(mainly the CMB); and Dark Energy (which may dominate the census, even
although it doesn't behave like matter at all!). It appears that the Universe
has a "flat" geometry, so that =1, and estimates
for the contributions from each of the 5 components are 5%, 0.3%, 30%,
0.01% and 65%, respectively.
Coverting into density requires having an estimate
of how fast the Universe is expanding, i.e. the Hubble constant (since that
goes into the definition of , as described in another
answer). Using a typical value for H0 the overall density
of the Universe turns out to be about 10-26kg/m3.
This corresponds to about 1011 times the mass of the Sun in
every cubic Megaparsec of volume. This value is uncertain both because the
value of isn't precisely known, and also because
the value of H0 isn't precisely known either. But it's certainly
the correct order of magnitude. You'd also get a proportionately lower
number if you wanted only the density in baryons, for example.
The total mass of the Universe, on the other hand, is not a very clear concept. The Universe is likely to be either infinite in volume, or so very large that it can be considered infinite for all practical purposes. That means that the total mass of the Universe is also infinite. The thing which can be well-defined though, is the mass within the observable part of the Universe. In other words we can ask: how much mass is contained within the volume that we can have observed since the Big Bang? The radius of the observable Universe is about 10,000 Megaparsec (or about 3 × 1026 metres). Using the above estimate for the total density this gives a total mass in the observable Universe of about 1054 kilogrammes. That's the best answer I can give for the mass of the Universe!
This is an email from 3 desperate undergrads ...
The topics we have to cover are: "Estimate the total energy in a comoving
volume and show that energy is not conserved. Where is the energy
going?"
Submitted by ForthEJ"AT"Cardiff.ac.uk 10/00
This is an excellent question!
There are several answers to this question, depending on the level of detail, or what you are prepared to accept as given. Let me give you 2. You can find more discussion in many standard undergraduate astronomy texts, in the cosmology section.
The first answer is that locally energy is always conserved, and that the rate of change of total energy density (in matter plus radiation plus whatever other kinds of fields might exist) is balanced by the work being done (per unit volume) by the pressure. So as long as you consider the total energy density (actually you need to use the correct relativistic quantity, which means adding in the contribution of pressure to the energy density), you find that at each point is is balanced by the work done by the pressure in expanding the volume.
However, you still have the problem of whether the global energy is conserved. CMB photons have their number per unit volume (or number density) reduced as the Universe expands, and the energy in each photon also gets reduced by the expansion. So the energy density in the CMB decreases faster than just the number density. In other words the energy density is falling off faster than the volume is increasing. So the total energy in CMB photons appears to be decreasing with time! The ultimate resolution to this problem is that the issue of global energy conservation in an infinite universe (or even a closed universe for that matter) is a thorny one within general relativity. If this bothers you, then rest assured that for all practical purposes the resolution of the problem is surely entirely irrelevant!
Do you know where I can find an estimate of the total mass of the
universe?
Submitted by cmcdonald"AT"regenstrief.org 10/00
If the Universe has "flat" or "open" geometry, then formally it has infinite volume, and therefore infinite mass. Something which is better defined is the mass within the "Observable Universe", which means the part of space from which we can have received light in the history of the Universe so far. This gets bigger every day!
The approximate answer is that the radius of the observable Universe is
currently estimated to be about 300 Ym (that's "yotta-metres", or
1024m, which is the largest SI prefix!). So you take that
number, cube it, and multiply by 4/3, to get the volume of
the whole sphere.
Then you have to decide what density you want to use. Are you only interested in luminous matter, or do you want to include all the baryons (regular stuff made of protons and neutrons)? Or do you want all the particle dark matter too? And what about the dark energy? If you include everything, then the average density in the Universe today is about 10-26kg/m3. And the mass in the observable Universe can be estimated accordingly.
There are several uncertainties and approximations here though - so don't expect your answer to be much better than an order of magnitude estimate!
I'm looking for a help to find the age of the universe.
When the Hubble constant is 20 km/s per million LY, and the formula to
calculate age is Age (t)=1/H, how can I find the answer as 15 billion years?
I did 1/20 which was 0.05, and I don't know how to find the right answer.
Submitted by yuriohara"AT"hotmail.com 12/00
This sounds like an attempt to get me to do your homework! While, I regularly give out free information for general questions on cosmology, there is a fee for doing homework!
Let me just try to offer a hint, which might help others who read this. The issue is units. If I told you that I was travelling for 30 hours at a speed of 3 miles per fortnight, and asked you to calculate how far I would get, then you wouldn't just divide 30 by 3 to get 10, right?
I have a (maybe primitive) image of a big bang that started as an
immense explosion in a relatively small space. The frontier of this
phenomina expanded and ... [abridged].
Submitted by thom.warmerdam"AT"mail.verizon.net 1/01
Your image of the Big Bang is far from primitive, but I'm afraid it is still incorrect. There is a very common misconception that the Big Bang is an "explosion" that happened at a point in space. This leads to some problems in understanding some things in cosmology, like the CMB photons. Let me try to paint you a correct picture.
First of all, no one knows exactly what happened to set the Universe expanding (although there is no shortage of ideas). What we mean by the Big Bang is that a model in which the Universe has been expanding, and used to be hotter and denser, provides a very good fit to a wide range of pieces of empirical evidence.
But let's imagine, for the sake of argument, that the Universe really did start with a singularity, which started expanding. The problem is that this singularity contains the whole Universe - so it's infinitely small and infinitely big at the same time! This is something which is very hard to picture. It turns out to be most helpful to think about a very large Universe which started expanding everywhere at once (and ignore the singularity aspect, since singularities by definition are places where your intuition tends to be in trouble!). So in the very early Universe everything was much closer together, but the volume of the Universe could still be infinite (if that's the sort of Universe we live in). Every point in the Universe expanded from every other point, with no special place being the "centre" of the "explosion".
I think if the word "explosion" was banned from all articles written on cosmology, then it would do much to alleviate this misconception!
Suppose that the universe is
much smaller than estimated. Would it not be possible, then, that the
light we receive from far away stars reach us after having made one or
two tours around our (suppesedly closed) universe?
Submitted by ulbusi"AT"tiscalinet.it 2/01
It's an interesting fact that in a Universe dominated by ordinary matter, and with enough density to have a "closed" geometry, you get get exactly once round the Universe in the time between the Big Bang and the Big Crunch! (Think of this as a hard-to-picture 3 dimensional analogy of going round the 2 dimensional surface of a sphere).
With the possible existence of "Dark Energy" or the "cosmological constant", it turns out that it is possible to traverse a closed Universe - and there never is a Big Crunch in fact (since the Universe continues to expand forever, driven by the energy density of the vacuum).
Best guesses for the sort of Universe in which we live make it very close to having "flat" geometry. In that case the Universe is really infinite in volume, and so you can't go round it (since it's radius is effectively infinite in size!).
It's still empirically possible, of course, for the Universe to be a little closed. But it is close enough to flat, that the possibility of things going all the way round the Universe remains basically a mathematical quirk, with little or no observational consequences.
we're doing a project in our astronomy class, and i had some basic
questions:
what EXACTLY is the cosmological principle? [abridged]
Submitted by sorceresscherish"AT"hotmail.com 4/01
Some more people wanting me to do their homework for them! All of those questions can easily be researched by surfing various web-sites. You could start by looking for ones that I link to on these pages. It's much better to try to find out for yourself through reading, rather than just asking someone!
But let me not be entirely unhelpful! I'll tackle your Cosmological Principle question.
That term was probably coined by a mathematical cosmologist called E.A. Milne in the 1930s. It's the idea that we don't live at a special place in the Universe. More specifically it is used, together with the observed isotropy of the Universe, to imply that the Universe must be statistically homeogenous (i.e. the same at all places, averaged over sufficiently large scales). In other words the Universe will look roughly the same, no matter where you are.
Have been fascinated by your web-site but having no knowledge of it could you
please tell me 'which atom makes up approx. 90% of the universe'.
Submitted by Glytrin"AT"aol.com 4/01
This question could mean at least a couple of different things, so to be safe let me answer both!
The normal stuff in the Universe (technically called "baryons") is, by number of particles, about 90% hydrogen, 10% helium and a fraction of a per cent heavier elements. If you ask what fraction by mass, then becuase helium weighs about four times as much as hydrogen you get about 3/4 of the mass of the baryons is in hydrogen, with about 1/4 in Helium, and only a trace amount of heavier stuff. So most of the normal matter in the Universe is simple hydrogen. The Earth has way more heavy elements than the average part of the Universe, because of gravitational and chemical settling in the formation of planets. So we're not made out of very common elements.
But various pieces of evidence point to the fact that normal matter (baryons) makes up only a small fraction of all the matter in the Universe. About 90% of the matter is in fact not baryons at all. It's not hydrogen, or helium or any other element. It's not made of protons and neutrons and electrons, but something else entirely. It has to interact very weakly with normal matter, exerting a gravitational force, but nothing much else. So we call this stuff "Cold Dark Matter", although we don't really know what it is!
Recent evidence also suggests that there's another kind of "stuff" in the Universe which isn't even matter at all! This stuff is called "Dark Energy", and we have even less idea of what it's nature truly is. But there appears to be about twice as much of this Dark Energy as there is Dark Matter.
So the Universe has only a small amount of baryons (only a tiny fraction of which consists of heavy elements necessary for life), and then even the Dark Matter isn't the dominant form of stuff. Why the Universe has chosen to be this way is one of the greatest mysteries known to modern science.
Why is it so
difficult to consider that space always has and always will exist and
that our little patch of it began, as some conjecture, from an
infinitesimal point due to some perturbing energy fluctuation.
Could it be possible that we might very well be at or near
ground zero and the fluctuations observed in the otherwise uniform
blackbody radiation seen in every direction suggest that possibilty?
Submitted by wjw"AT"bellsouth.net 5/01
One way to think about this is the following. The Hubble expansion law, discovered about 75 years ago, is that the velocity of recession is proportional to the distance. So what kind of "explosion" does that represent? In fact, if you think about it for a while (draw a bunch of dots at two difference times if it helps), this is precisely what you get in uniform expansion. If every distance gets multiplied by some constant at each time "frame", then more distant things are moving proportionally further away from you. But uniform expansion doesn't require a centre -- the opposite really. In uniform expansion everything is moving away from everything else, and so there's no special centre. It might look like things are moving away from you, but if speed is proportional to distance, then every other observer would see things moving away from them too.
So the observation of the Hubble expansion really fits with a picture in which everything is expanding from everything else. There's no centre, and need to think of it as an explosion localised in space.
Maybe I just don't understand infinity but, if
the universe is expanding, as I expect it is, where is all of the matter
going as the density of the entire universe decreases? Or does infinity
preclude the use of the word "entire"?
Submitted by jmorgan"AT"logantele.com 5/01
You are right! Infinity is a very tricky business.
One way to see this is to try to understand that if you have an infinite amount of something, and then you add a little bit, then you have exactly as much as you started with - an infinite amount! In otherwords if you add a finite number to infinity you still have infinity. And even if you multiply infinity by something you still get infinity. This is true even for the highest number you can think of (and the only exception is if you multiply it by zero!).
Thinking about it ths way, if the Universe is genuinely infinite and it's expanding, then everything used to be closer together, but that doesn't mean it was smaller! It has been infinite from the beginning. At the very beginning, if there was a singularity (and to tell you the truth, most cosmologists suspect you can't push things back that far) then everything was at one point. So the Universe would have been both infinite in volume, and have no volume at the same time. This is the problem of multiplying zero by infinity - which one wins?
Let's face it, at the moment no one has a clue how to picture the very beginning of the Universe, infinite or not!
I guess you'll agree with "there is no perpetuum mobile",
meaning here: there is no lossless process in Nature.
Why then did Einstein & Hubble, as scientists, accept fotons to
travel billions of lightyears _without_ energy loss (= redshift,
by Planck's E = h.nu with frequency 'nu' lowering: redshift) --
but rather assumed interstellar space to be 'pure vacuum' sothat
no loss is possible --> hence the Doppler-shift interpretation,
thus the expanding universe, hence by time-inversal the Big-Bang.
So: is light-propagation the ONLY perpetuum mobile in Nature ?-)
Submitted by nico.benschop"AT"philips.com 9/01
Photons travelling large distances through the expanding Universe do lose energy, since that's what the redshift is. The wavelength of the photons gets shifted towards lower energies. There have been various ideas about how maybe the light from quasars loses energy from some other process, so that quasars don;t havw to be at their cosmologically assumed distances. But such ideas, like "tired light" haven't fitted the data well for decades, as I've discussed on this page before.
The reasons to believe in an expanding universe are basically two-fold. Firstly you observe bigger redshifts for apparently more distant objects, and the simplest explanation is just that they're moving away from you at a speed which increases with the distance. This implies a framework in which the Universe as a whole is expanding uniformly in all directions. Which brings us to the second part - that you figure out what that means for observations of other astrophysical phenomena and see whether there's some contradiction or something that doesn't fit. The fact there is that the picture is entirely self-consistent. Almost uncountable amounts of observational data involving a huge number of different kinds of study (distant galaxies, clusters of galaxies, gravitational lensing, distant supernovae, the CMB anisotropies, quasar absorption clouds, abundance of the light elements, blackbody spectrum of the CMB, etc., etc.) make sense within the context of the expanding Universe picture.
This basic picture fits so well that we can start trying to determine more details than just this framework. The focus right now is on trying to figure out precisely what sort of expanding universe we live in.
How does the CBR theory reconcile with the the following points and
questions...
1. the assumption/theory/fact? that nothing can exceed the speed of
light,
2. given the universe has expanded rapidly from a pinhead of matter to
its present size via the big bang,
3. that CBR was generated immediately/shortly after the big bang,
4. the earth (being our current point of observation) is somewhere
inside the sphere? of the still expanding universe.
Submitted by frankhamersley"AT"hotmail.com 11/01
There are more full answers to essentally this same questions elsewhere on this very page!
For now let me just say that points 1. and 3. are correct, that 4. is true for everything in the Universe (by definition) including us obviously, but that point 2. is not a correct statement. There have always been regions of the Universe farther away than light has been able to travel in the age up to that point. That applies today and equally well to early times in cosmic history. The CMB photons that we see today came from such parts of the Universe.
There is a firm belief now that the dark-matter in the universe is as
ubiquitous as CBMR. ... My question is whether E=MxC-squared is
operative only in the 4-dimensional physical universe, while the
dark-matter seems to be belong to a higher dimension and yet as
pervasive as CBMR. [abridged]
Submitted by pnkumar"AT"csnpl.ren.nic.in 11/01
I think you are ascribing way too much mystery to the dark matter. Think of it simply as a form of matter that's not very luminous - "unshiny stuff" I like to call it! There's no reason to believe that it doesn't conform to the normal laws of physics (like E=m.c2). Indeed we only know about the existence of this form of matter through its gravitational influence. So we know that it feels (and creates) the force of gravity just like any other kind of matter. But it doesn't seem to have any electromagnetic interactions (otherwise it would be way easier to detect). In that regard it's like the neutrino, and several other particles, which we know a lot about. But those already known particles can't be the dark matter, since they have the wrong masses.
Most cosmologists think that the dominant form of dark matter is simply some as yet undiscovered kind of particle. Or at least "undiscovered" in the sense that we don't know any of its properties, even although we know it's there. All we do know about it is roughly how much of it there is, that it experiences the gravitational force, and that it's not very shiny!
...I am interested in writing an article on dark matter and dark
energy. Would it be all right if I sent a few questions? [abridged]
Submitted by a.kay"AT"fisheries.ubc.ca 12/01
You could start by reading the answers to some of the relevant questions on these pages.
Another place to try is the CDMS (Cryogenic Dark Matter Search) experiment education page. And there are many more resources on the web.
... I envisioned a revolutionary theory on the formation of
galaxies and matter. To begin with nobody to date has
observed the primordial cosmic clouds of dust and gas
required for stars to have been formed before they
condensed into galaxies. ... I've gone on to propose that these
"gravitational fragments" played a major role in the
formation of matter. ...
...It is plain to see that if massive black
holes were ejected from the Big Bang as a giant grape
shot space would have expanded naturally in keeping
with the General Theory of Relativity.
Submitted by rwpcuus"AT"yahoo.com 12/01
Let me say that I quite often get emails from people suggesting alternative theories for the formation, evolution or structure of the Universe. This one contained many more interesting ideas than most.
One of the first statements is wrong - since the CMB anisotropies give very clear evidence that there were slight overdensities in the early Universe, of just the right amplitude for gravity to have grown all the structure we see. But the ideas of cosmic centres around which structure gew are very reminiscent of cosmic-string seeded ideas which were popular with some cosmologists in the 1980s, but ultimately proved not to explain more recent CMB anisotropy results. And the last idea involving cosmic expnasion through some kind of ejection is not too dissimilar from "kinetic relativity" of the 1930s.
But if you want frank advice from me, it has to be this. Understanding, in detail, the formation of structure in the Universe, is not an easy matter. If you want to make any sort of valuable contribution to this area, then there is no substitute for an awful lot of reading and study. Go through some good popular books on the subject, and then work your way up to the more technical stuff. Once you are able to understand the average paper published in the cosmological literature, and you still disagree with the conventional picture, let me know your detailed objections. Sorry if this sounds dismissive, but look at it this way. I wouldn't seriously cosnider myself qualified to build a highway bridge, or perform surgery, without several years of formal study. Put it another way. I don't even take half the stuff I read ion the scientific literature terrribly seriously, and it's all written by people with Ph.Ds. from famous universities!
What is vacuum energy? I know it is used to explain Inflation.
Specifically how can there be a high pressure in a vacuum?
Submitted by rreeves"AT"winfirst.com 12/01
Let me be frank here, and state that this stuff is hard to understand from the viewpoint of everyday common-or-garden experience!
To fully appreciate what's going on, you may need a deeper understanding of General Relativity than I'm likely to be able to impart to you in a few sentences! But nevertheless, let me try a brief answer.
The first point is that pressure of very fast objects can act as a source of gravity, just like mass does. Typical radiation, like the CMB, actually exerts twice as much gravitational force per unit volume than Newton might have guessed, because of this fact.
The second point is that empty space, "the vacuum", is something we know much less about than we'd like. Once physicists understood that particlce-antiparticle pairs can be blinking in and out of existence all the time, then it was no longer obvious that the energy density of the vacuum was zero. It turns out that the vacuum has to have a pressure which is negative and equal in magnitude to its energy density (that's a necessary consequence of the structure of space-time, effectively). iSo if the energy density is zero, then everything seems OK, since the pressure is then zero too.
But if there's even a tiny little bit of non-zero energy density in space which is devoid of matter or radiation, then there's also a negative pressure there. It's dwarfed by normal forces over small length sclaes, but it builds up over cosmological scales, so that it can dominate the dynamics of the Universe as a whole. Going back to the first point above, it turns out that a vacuum (with pressure equal in magnitude to its energy density, but negative) leads to a gravitational repulsion. So the Universe behaves very differently if there's a non-zero vacuum energy - or what Einstein called the "cosmological constant" is non-zero.
And at the moment that's precisely the kind of universe we think we live in!
I have read enough books (Greene's The Elegant Universe,
Smolin's Three Roads to Quantum Gravity and others) to have a good idea
of the Guth expansion, but nowhere can I find the answer to what caused
the expansion to stop. [abridged]
Submitted by loedvdh"AT"vgernet.net 2/02
This is a very good question!
Inflation is an idea which has several appealing consequences, and so is quite popular with cosmology theorists. However, there are also some shortcomings. The main one is that it is really just a good idea, looking for a specific theory! In other words, no one knows precisely what kind of inflationary model may describe what happened in our Universe.
So the simple answer to your question is "nobody knows"! It's clearly a requirement that the epoch of extremely rapid expansion has to stop at some point. So all reasonable inflationary models have to build in a way of stopping this inflation, as well as generating all the matter in the Universe from the fields that existed during inflation, and then turning into a run-of-the-mill expanding Universe.
The hope is that one day a single inflationary theory will come to the fore, through a combination of empirical evidence and theoretical work perhaps. Then everything will be clear!
Also, what do you think we could say if we saw a blue shift in light arriving
from distant galaxies instead of a red? What would we say about the beginning
and ending of our universe?
Submitted by gte878n"AT"prism.gatech.edu 3/02
In fact some nearby galaxies do have blueshifts! That's because they happen to be coming towards us. Every galaxy has its own local or "peculiar" motion. For ditant galaxies the expension speed dwarfs these "peculiar" motions, and so you can ignore them for most practical purposes. But for nearby galaxies like Andromeda (M31), their motion towards us is bigger than the motion which could be casued by the expansion of the space between us, simply because they are so close.
However, these local blueshifts tell us nothing very fundamental about the nature of the Universe.
Howerer, if we were to observe very distant galaxies blueshifted, then that would indicate something was quite wrong with our picture (e.g. that Universe had been contracting in the past). So far we've never seen anything with a large blueshift which appears to be very distant. All distant objects have a redshift, with that redshift increasing with distance away - hence our picture of the uniformly expanding Universe.
Interestingly, if we lived in a universe which stopped expanding and started contracting again (and let me state clearly that we do not currently think that it's likely we live in such a Universe), then there would come a time in the future when all the galaxies would become blueshifted. They'd rush faster and fast towards us until we all disappeared in a Big Crunch!
Hypothesis: The distribution of large scale cosmic structures follows the
form of a 4th dimensional polytope [abridged]
Submitted by ArtCatsDOTNet"AT"aol.com 4/02
We know from surveys of regions of the Universe, that objects are not distributed in such a geometrically simple way. There are objects all over the place, and they are clustered together over a wide range of scales. There are groups of galaxies clumped into clusters, which lie at the intersections of "filaments", and with low contrast "voids" separated by "walls", etc. The distribution looks a bit "foamy", but the "voids" are far from empty, just under-dense compared with the clusters.
Cosmologists have developed many statistical tools to help quantify and understand this clustering. One tool which is sometimes useful is to use the so-called "Voronoi tesselation", which is a little like what you describe. Although galaxies don't lie along the sides of such polyghedra, the picture can still be used to help describe some of the average properties of the distribution. If you are interested in this topic I suggest you search for things on the web relating to Voronoi foams and cosmology.
Could you please explain what you meant by curved geometry, and what the
universe would be like if it was curved.
Submitted by katharos1.scotland"AT"tinyworld.co.uk 4/02
It's easiest to think about this in 2 dimensions (where your brain can easily visualize things), and then extend that to 3 dimensions by analogy.
In 2D, there are 3 possible ways that things can be curved. Either the space is flat, or it's like the surface of a sphere (which is called "positively curved"), or like the inside of a trupmet or the surface of a saddle (curved one way in one direction, but the opposite way at right angles, which is called "negatively curved").
In flat space you know that the angles of a triangle add up to 180 degrees. And that if you start with a straight line, there's only one parallel line which goes through a specified point. But if space is positively curved then the angles of a triangle add up to more than 180 degrees (think about drawing a triangle on the surface of a sphere), and there are no parallel lines! In negatively curved space, the angles add up to less than 180 degrees and there's an infinite number of parallel lines!
In 3D space, you have to imagine things curved in some hypothetical 4th dimension, which obviously you can't see. But you can still do experiments to figure out what kind of space you live in. For example you can try constructing a huge triangle and then measure the angles. It turns out that you can perform just such an experiments using the characteristic angular size of variations on the microwave sky. The answer seems to be that the geometry is very close to flat, just like Euclid described thousands of years ago!
It's the material contents of the Universe that cause the curvature. A purely empty universe would have negative curvature. So in order for space to have nearly flat geometry, there needs to be enough stuff to make the curvature close to zero. Since there isn't enough normal matter around, or even Dark Matter, then that means there has to be another component of stuff filling the Universe, and contributing to the curvature. This mysterious stuff is sometimes referred to as Dark Energy. And we think it makes up about two thirds of the total mass-energy content of the Universe.
You mention several times in answers to questions that the early universe
was not smaller than today, indeed that it can be considered to be infinite
in size. Can you explain this further? I cannot understand how an
infinite-sized universe could have emerged from a singularity.
Submitted by sa3910"AT"mail.eclipse.co.uk 05/02
The simplest view of the earliest history of the Universe is that it expanded from an intial singularity. That means that the whole Universe used to have infinite density. Or in other words, all of infinite space used to be in one place!
Although I said this was the simplest picture of the beginning of the Universe, I didn't claim that it was either (a) considered to be the most likely scenario or (b) easy to get your head round!
Although I cannot speak for all cosmologists, I suspect that few of them believe that the beginnings of the Universe were quite so straightforward. Once things get close enough together you need a quantum theory to describe the whole Universe, and such a theory does not currently exist. One of the most promising avenues is something that would come out of string theory - but really no one has much of a clue right now.
If I personally had to put money on anything it would be a picture something along the following lines. At the very earliest times in the history of the Universe things were very simple, but in a way which we currently do not understand, with notions like time and space being replaced with something else. Out of that a small part of the Universe inflated to enormous size very rapidly for a while, and ended up expanding in the "normal" way. We live in a fairly normal part of that expanding region. And hopefully there are observational signatures which will allow us to piece together some information about the underlying concepts which made all this happen. In fact, I would
... I'm left with a main problem concerning the Matter Power Spectrum
Structure formation theories based on inflation predict (nearly) scale
invariant adiabatic density perturbations and permit to define their
initial HZ spectrum P(k). Recently LSS and CMB data allowed to measure
the current (z=3D0) Power Spectrum of density fluctuations. I do not
understand how the shape of this spectrum pops up and agrees with
theory ... And one more question: Can the Matter PS be linked or extrapolated
to the CMB PS?
Submitted by rkail"AT"swissonline.ch 8/02
The basic idea is that inflation (or whatever) gives you a scale-invariant initial power spectrum. Then the magic of the expanding Universe and the domination by dark matter does the rest, and makes a spectrum of matter perturbations which closely matches observations. The "cold dark matter" model gets this right without trying, which has always been its major success. Then by tuning to get it exactly right you can constrain some of the parameters of the model in detail.
The basic idea is that P(k)k turns over as the Universe
goes from radiation to matter domination because of the different growth rates
of perturbations inside the "horizon" in a radiation vs matter dominated
universe. The calculation can be found in any standard text on cosmology,
e.g. the ones by Peebles, Peacock or Padmanabhan.
As for your other question, there is no unique relationship between the matter power spectrum and the CMB power spectrum. They each depend differently on the underlying parameters of the model. So if you know one, you don't know the other. But that's a good thing, since if you measure both, then you've learned a lot more!
many years ago on a TV science documentary about the big-bang, they played
a sound which was claimed to be the echo of the big bang adjusted to a
human hearing range, all I can remember from the remnants of my memory is
that the played sound was a gently modulating tone around 5 Hz or there
abouts, have you an idea where I could look for this information
Submitted by colin.penney"AT"uk.goldschmidt.com 06/02
I've had basically this same question before, so you should search above for my inadequate answers!).
I'm assuming that they just mocked something up for the TV documentary, and I can imagine a couple of different things that you could imagine doing that you could very loosely call "the sound of the Cosmos" or some such.
If anyone knows of something which exists on a web-page already, I'd be interested to hear it.
My question is "How can the Universe be 14 billion years old when we can
see stars whose light is 11 billion years old?"
[abridged]
Submitted by Stuart_Casey"AT"aporter.com 10/02
From the rest of this question, it seems that there is some confusion about distances, times and expansion. So perhaps it will help if I explain as clearly as I can.
The Universe is expanding. So objects further and further from us have their light more and more redshifted.
For very distant objects, we use this redshift as a stand-in for distance. So when some newspaper report says "the light left this galaxy 11 billion years ago" or "the quasar is 10 billion light years away", in fact those numbers come from turning the measured redshift into a distance (or light travel time) given a favourite model for exactly how the Universe has been expanding.
So whenever such numbers are given, they have to be consistent with the expanding picture, since they were derived by assuming it in the first place!
The other thing to remember is that we see the objects as they were when the light left them. So an object 11 billion light years away is seen as it was 11 billion years ago. The furthest objects we can see are obviously the light travel time in the age of the Universe (reckoned to be something like 14 billion light years).
When the light left the distant object, we were in fact much closer together than we are now. But there's no direct way to tell how distant an object is "now". So in fact all astronomical information is constrained to come from times very nearly equal to the light travel time between us.
So it would really be impossible for the distance (in light years) of an object to be inconsistent with the age assumed for the Universe, since those are really just the same thing. (On the other hand it is possible to estimate the age of some objects, globular clusters for example, and thereby determine a lower limit for the age of the Universe - and so far there's no indication of anything older than the models are comfortable with.)
why is it that the scientific
community keep sticking to the bigbang theory,when it could be wrong?
Submitted by Bravo_Lawrence"AT"windalco.com 10/02
This is a good question, and gets at the heart of what Science is.
The answer is that one should only accept that something is a good explanation if there is good evidence. The Big Bang picture rests on very good evidence, specifically: the expansion of the Universe; the thermal nature of the Cosmic Microwave Background; the abundance of the light elements; the evolution of the properties of galaxies over time; and the successes of structure formation models within this picture. If the edifice of the Big Bang wasn't so strong (and hadn't been gaining in strength since introduced about 40 years ago) then there would be no reason to take it seriously.
If however there was a
single object which exploded,what existed outside of that object,was it
just infinite vacuum? If so,how did that vacuum come into existence? and
how old was that vacuum before the big bang?.Was time unmeasurable before
the big bang?
Submitted by Bravo_Lawrence"AT"windalco.com 10/02
There are two fundamental problem here. Firstly, the "Big Bang" is a model for how the Universe has been expanding and cooling from early times, which says nothing about what happened in the first instant. Secondly, the usual picture within the context of curved space-time (i.e. the theory of garvity we call General Relativity) has the whole Universe expanding, rather than an object within the Universe. It is probably helpful to try to dispell all notions of an "explosion" from your mental image of the earliest times in the history of the Universe. It is (let's be honest here!) quite hard to picture an infinite expanding Universe which was once all close together! But that's something like the right picture.
is it
theoretically possible for two points within the universe (that we can
perceive from our vantage point) to be moving away from each other at a
speed greater than the speed of light. And - are these two points
completely inaccessible and theoretically unknown to each other?
[abridged]
Submitted by procheck"AT"procheck.cc 11/02
The picture you describe sounds like the boundary of the "observable Universe", which is an imaginary sphere around us, expanding at the speed of light. We don't know about anything outside this region, since the Universe has a finite age, and information can't travel faster than the speed of light. But every year we see another light year's worth of the Universe.
The parts of that imaginary sphere which are at opposite sides of the sky (for us) are moving apart from each other at faster than the speed of light. But that's not actual "stuff" moving, but just the mathematical description of the edge of our observable region.
However, in the "inflationary universe" picture, there was a period of rapid expansion in the early history of the Universe, in which the expansion was faster than the speed of light. That allows for an initially small region to have blown up to be much bigger than what appears to be the size of the observable Universe today. One of the things this helps to explain is why regions on opposite sides of our observed sky can have the same CMB temperature, even although they appear never to have been in "causal contact" (i.e. contact at slower than light speed) with each other.
So certainly it's possible to have regions moving apart faster than the speed of light. And certainly it's possible to have the structure of spacetime outside our observable region have an influence on the sort of universe that we live in.
What are the chances that 'dark matter' and 'dark energy' will suffer
the same fate as the ether?
Submitted by jsnyder527"AT"hotmail.com 2/03
I assume this means what's the chance that they'll go away?
Remember that the CMB is in a sense the "ether", since we can in fact tell what speed we're going through the sea of CMB photons, by measuring the CMB dipole - so the ether came back!
But to return to the question, the evidence for dark matter is extremely robust at this point. It is very clear that over a wide range of (large) scales there is more gravitating matter than accounted for by the luminous stuff. And it is also clear that this matter must be mainly non-baryonic (i.e. made of something other than protons and neutrons). The "missing mass" problem goes back about 50 years, and has only become clearer with time.
The evidence for Dark Energy has been amassing since about the mid-1980s. There are now several separate lines of evidence (including from CMB anisotropies) indicating that most of the "stuff" in the Universe isn't even matter, but made of something with negative pressure. Exactly what this is remains to be seen, but there are some promising methods of studying its effects in more detail in the near future. The chances that it will go away altogether seems quite remote. But it's true to say that the evidence is not nearly as secure as it is for dark matter.
Recently, the WMAP probe confirmed previous experiments that showed "dark
energy" to be the major constituent of the Universe. Supernova red-shift
observations indicate that dark energy's contribution to the Universe is
growing because space is expanding. Since dark energy is basically the
energy of "empty" space, and since the amount of space is growing, the total
amount of dark energy is growing. Does this violate the law of conservation
of energy in the traditional sense? If not, from where is the energy
coming?
Submitted by Peter.R.Menge"AT"saint-gobain.com 3/03
The answer to this question is "no!" Despite how bizarre the dark energy appears to be, it does not in fact violate conservation of energy. The ultimate reason for this is that it is entirely consistent with General Relativity, which effectively has energy conservation built into it.
One way to understand what is going on is to remember that you have to do "work" on something which is under pressure if you want to shrink its volume (work done = p dV). The vacuum has negative pressure, and therefore it does work on its surroundings when it expands. This precisely balances the increase in energy in the volume, and hence locally energy is conserved. However, the global amount of energy is another thing entirely!
Are we using the same frame of reference for measuring the presently
observed radiation and estimating its original frequency? Indeed, in
talking about cosmology in general, what do statements about events in
time and space mean when spacetime is continually changing and being
subjected to huge concentrations of energy and huge curvatures?
Submitted by ianw"AT"netspace.net.au 3/03
You are right that one has to be very careful in talking about times and distances in cosmology! Rest assured that when real cosmological calculations are done, that all the effects of expansion and curvature are taken into account. What this means is that the answers often depend on the precise cosmological model being used (i.e. the parameters that describe our Universe).
Fortunately it looks like the Universe has close to flat geometry, so there's no real need to worry about large-scale curvature effects. Space is just like Euclid imagined it, except of course that it's expanding. The expansion of space means that you have to take care to define exactly what you mean by lengths. Cosmologists often deal with "comoving" lengths, which means lengths which have had the expansion of the Universe divided out. Or in other words, what the length would be as measured at the present day. For objects which are separating along with the expansion, true physical distances were smaller than comoving distances in the past, and will be larger in the future.
By using comoving distances for a specific cosmological model it is possible to be quite precise about the meaning of distances in cosmology. However, when one reads statements in popular accounts, like "the quasar is 10 billion light years away", one is never entirely sure what is meant!
How can it be said that the universe is expanding today when the
data that this statement is based on reflects what was going on billions
of years ago?
Submitted by erckjcbsen"AT"att.net 3/03
The original data (Hubble's) for showing that the Universe was expanding came from much, much closer than that. All galaxies other than the closest few are redshifted. So you "only" need to go out to a few 10s of millions of light years in order to test that the Universe is expanding. Relative to the age of the Universe (more than 10 billion years), this is a relatively local scale. Hence we can be pretty confident that we know how the Universe is expanding today. Then when we look to much greater distances (and hence probe earlier times) we can find out about how the Universe was expanding in the past. This is how we have discovered that the Universe has been accelerating over the last few billion years.
How much of our evidence for the dark stuff is direct? How
much on a (perhaps flawed) understanding of how to extrapolate the laws
of gravitation from the laboratory of solar system sized objects, to
large scale gravitating objects like galaxy clusters, or galaxy centers?
How far can we safely extrapolate? This should clarify my original
question. If you had to give odds, what would you say are the chances
that we are wrong about the dark stuff?
Submitted by jsnyder527"AT"hotmail.com 3/03
Let me try to give you my frank opinion here. There is no doubt that there is a lot of "unshiny stuff" in the Universe. The question is just how much is there, and the answer, traced by gravity, is that there's really quite a lot. This evidence is very direct, and has been there since the 1940s, getting stronger by the decade. There have been attempts to invoke alternative theories of gravity to explain the results without the need for dark matter, but they have been quite unsuccessful. And what's wrong with "unshiny matter"? Why should a whole new theory for gravity be any more appealing?
The somewhat surprising thing is that there's good evidence (from the abundance of the light elements) that there's too much matter to be baryons (i.e. normal stuff). So it's presumably some kind of particle that interacts weakly, so it's only easy to detect through its gravity. This may seem a bit uncomfortable, but I think if we can swallow that neutrinos exist and are passing through you at the rate of maybe 1015 per second, then some other particle can't be that hard to accept! We now know that neutrinos have mass, and if they were a bit heavier they could be the dark matter. So we just need another particle streaming through the Universe that's heavier than a neutrino. I think this is actually not particularly difficult to believe.
What's much more surprising is the Dark Energy, which seems to dominate the total budget of the Universe. There's no obvious reason why that should exist at a level just a factor of 2 or 3 times more than the matter. It might just be the energy density of the vacuum, but if so we're quite surprised at its value. Or of course it might be something else entirely, that we just don't understand yet. The evidence has been growing steadily since (I would say) the late 1980s. The combination of the supernovae results and the CMB results on top of the weaker indications from before, mean that we have to take the idea of Dark Energy very seriously. Ugly or not!
Recently some of my friends have become enthralled by the notion of
"parallel universes" ... Could you please point me to more
information on the subject and/or give your own opinion?
Submitted by christalynn50"AT"hotmail.com 4/03
You may have seen the recent article in Scientific American by Max Tegmark. There's more discussion on parallel universes at his web-site: here.
The basic point is that the concept of different "observable universes" is very solid, but the different regions can't be very different, since they are all part of the msame underlying model and certainly obey the same laws of physics. On the other hand the idea of actual "multiple universes" is much more speculative. Scientists disagree on whether there is any use talking about such concepts, and if there is, then should it be kept for the coffee room? In other words is it really science? Can one imagine experimental evidence for or against such a picture?
Everyone agrees that it's fun to speculate about such ideas! And since there no general agreement on the "right" thing to think, then you're free to imagine whatever you like!
If the universe is infinite, and since our horizon is only ~10^10
light years, then straightforward calculations by Max Tegmark imply that
there are only 10^80 distinct ways to arrange sub-atomic particles
within our observable universe. Therefore, our entire observable
universe MUST start to repeat (ie, duplicate) on a scale ~10^(10^110)
light years. ie, a "parallel" universe where a duplicate of me is
typing this email. Tegmark's reasoning appears straightforward ...
is there any refutation to it, at all ??
Submitted by therman1"AT"mindspring.com 4/03
My own estimate would be a number larger than that, but the point is that the calculation is finite. Therefore if the Universe is genuinely infinite, then there would indeed be effectively copies of everything somewhere!
However, speculating about what goes on beyond the observable Universe is really just speculation! We don't know much of anything on that subject. So I'm prefectly free to imagine that there's something more complicated about the Universe which makes it finite but unbounded in some way. So I don't necessarily have to hurt my head by thinking about things which involve infinity if I don't want to!
where did this extremely dense extremely hot condition before big bang
originate from?what was before big bang?was it just the platform of time and
space or something else?
Submitted by shamsmonaas"AT"yahoo.com 7/03
In the picture which most cosmologists have there was nothing before the Big Bang, because time itself didn't really exist. But there are also more speculative ideas in which, before the Big Bang, there were previous phases in the history of the Universe. The main thing to realise is that we know a lot about the Universe today, and by studying things like the CMB we can push back our understanding to very early times - but it becomes increasingly shaky to talk about things as you approach t=0. So right now there are no defnite answers to your question!
what were the mean energies per particle, and the age and temp of the
universe, when the electrons and positrons annihilated each other?
Submitted by Chloalip"AT"btopenworld.com 8/03
The approximate answer is that this happened when the average kinetic energies of particles was about equal to the rest mass equivalent of an electron or positron. So in particle physics units that's about an MeV. You get the temperature just by converting this to Kelvin, which gives you around 1010K. The time depends somewhat on the model, but is around a few seconds.
I'm currently reading "Three Roads to Quantum Gravity" by Lee Smolin.
On page 30, he states that many cosmologists argue that the size of the
universe is 100 billion lightyears.
In the same paragraph he also states that the Universe is only ~14
billion years old.
He also states that the reasoning behind the 100 billion lightyear
figure is beyond the scope of his book.
How can the Universe expand 100 billion lightyears in only 14 billion
years without travelling faster than light?
Submitted by gregl"AT"debut.to 9/03
There's nothing very peculiar going on here, just the expansion of the Universe!
The best estimates for the age of the Universe are about 14 billion years. Distances in cosmology are complicated by the fact that the Universe is exapnding, and so you have to be careful to define precisely what you mean. The "size of the observable Universe" can be thought of as the answer to a question like: "if I started at time zero moving at the speed of light in a straight line, then how far would I have gotten by now?" The answer is a bit more than the age of the Universe times the speed of light, because the space that you're moving in has been stretching in the time it takes you to complete the journey. The precise answer depends on how this stretching changes with time. The current best picture is that the Universe was decelerating until relatively recently (on some cosmic scale at least!) when it started to accelerate again. Putting in the best estimates for this variation of the expansion over the last 14 billion years gives a factor of around 3.5. Then if you want the diameter rather than the radius of the observable Universe, you get a number close to 100 billion light years.
If the galaxies are undergoing redshift, why are not the heavens
shades of red everywhere we look when we are outside the earth's
atmosphere?
Submitted by tmgulland"AT"hotmail.com 10/03
Red-shift means that all the wavelengths are stretched to be longer, not that all the light becomes red. Galaxies have energy over a wide range of wavelengths, so if the rest-frame blue gets shifted to be red, then the rest-frame ultra-violet gets shifted to be blue, etc. The shade that a galaxy would appear depends on details of the shape of its spectrum, as well as how red-shifted it is.
If spectra well featureless, then we wouldn't be able to tell that things were Doppler shifted. The way that we tell is by looking for spectral lines, i.e. specific patterns of absorption or emission at wavelengths determined by particular atoms or molecules in the object. So a high redshift galaxy might have the "Lyman alpha" line of hydrogen appearing not around 120 nanometres but at, say, 500 nanometres (and known lines at all other wavelengths would be similarly stretched). By recognizing characteristic features in the spectra of nearby galaxies and seeing that the same patterns occur at longer and longer wavelengths in more and more distant galaxies, we can conclude that the Universe is expanding.
But in a sense the entire sky is quite red. The most distant source of light that we can observe is the CMB. That was emitted at optical-type wavelengths, but has been redshifted all the way to microwaves!
I am a poet, not a physicist, but we poets have a long history of proposing
cosmologies. I hope you will allow me a few minutes, even if you do it just
for laughs, to hypothesize a cosmology, a revision of the Big Bang that
might be called the Bigger Bang.
Begin with a question: what should the universe look like if tachyons exist?
[abridged]
Submitted by ws"AT"pop.socialstudies.com 10/03
This is an interesting question. I am tempted to answer "it wouldn't look like anything, because the Universe wouldn't exist if tachyons did"! However, let me try to say a little more than that.
Tachyone are hypothetical particles with imaginary mass which move faster than the speed of light. When people have tried to study their consequences, things get pretty silly pretty quickly! Hence most physicists regard them as being of only theroretical interest at best, although it is probably also true to say that there is no fundamental proof of their non-existence.
But this hasn't stopped them entiring the popular consciousness through being a useful plot contrivance used to get round problems of the vastness of space in science fiction. And they have also entered "New Age" literature, as you can read about in the excellent Skeptical Dictionary. You can also read more about tachyons in general at many places on the web (e.g. here.
The jist of your idea, of the Universe being created out of the "wavefront" of tachyons made at the Big Bang has some similarities with the "kinematic relativity" idea of E.A. Milne, who was one of the fathers of modern cosmology. You can also read more about Milne and his ideas on the web. Although he was attempting to develop a cosmology which didn't rely on General Relativity, he developed a bunch of the key ideas in our current cosmological picture. So, who knows, maybe something useful might come out of thinking about even stranger ideas, like faster than light particles at the Big Bang!
I have a bit of a conceptual problem with the current model of CMB because
when I try to visualize it issuing from beyond the furthest galaxies, and
also visualize the fact, apparent in Olbers' paradox, that the galactic
clusters are so numerous as to preclude that there be any path from the
centre of the universe to the perimeter that is not obstructed by hot
matter, then I am left wondering why CMB isn't all absorbed.
Submitted by tmgulland"AT"hotmail.com 11/03
Firstly, there's no "centre of the universe"! Everyone can think of themselves as the centre if they like though. They're all equivelent.
Secondly, the amount of absorption through a galaxy cluster is something like a per cent. And the hot regions of galaxy clusters certainly don't cover the whole sky, but only a very small fraction. So the total amount of absorption (actually scattering of the photons to higher energies) through clusters is somewhere around one part in a million.
Since the universe is expanding, does that not imply at least
philosophically, that it is indeed finite? You cant add magnitude to
something that is infinte (for a start it defeats the purpose of having a
notion of infinity) since you cannot identify the boundary of an infinite
domain upon which to do the addition.
Submitted by gterry"AT"au1.ibm.com 12/03
Infinities are things which make your head hurt if you think about them too long!
But certainly there's no mathematical problem imagining something which is infinite and expanding. If you take an infinite thing and multiply it by a constant, then it's still infinite. To a mathematician the new thing is precisely as big as the old thing. However, to a physicist, if you take an infinite Universe and move everything further apart, then it's bigger!
If you apply the Hubble expansion over a infinite universe, dont you
then get galaxies at the extremities of the universe moving away from us at
faster than the speed of light?
Submitted by gterry"AT"au1.ibm.com 12/03
Yes!
Although you need to be careful about how you define distances and times in an expanding Universe, so that you use a meaningful concept of speed. This is all taken care of within general relativity, which is the framework which underlies all modern cosmological models.
Are we seeing in the light from
these distances objects say 1 billion light years the reflection of the
actual object or the object as it was 1 billion light years ago. If we were
to observe deep space in our real time is it not possible for the "spacescape"
(for lack of a better term), to have changed i.e.stars die or galaxies folding
into black holes ect? So what we are seeing now may all be changed in our
reality?
Submitted by pareynolds"AT"sasktel.net 01/04
It is certainly the case, that since light has a finite speed, that it takes time from the light to reach us from distant objects. For example, an object 1 billion light years away is seen as it was 1 billion years ago. Hence, even if we could build a rocket which can travel near the speed of light, it would take us another billion years to reach the object and by then it would be 2 billion years older than it appeared to be when we first saw it! (this ignores the fact that the Universe is expanding during the time that the light and our spaceship make their journeys, but that just makes it a little harder, and certainly doesn't change the basic picture).
You can bet that if we really could do such a thing, we'd find objects to be very different than how they appear now. As we make the journey towards them we'll intercept photons that left later and later, of course. And when we're about half way there, we'll see the object as it was when we left our own Galaxy!
[referring to my description aboce of inflation allowing parts of the
Universe to expand away from each other faster than the speed of light
Really!? Can you elaborate? If we have two heavy bodies
placed in two locations wich move away from each other with v=c,
which energy will have one of them relative to the other one?
Infinite?? With infinite gravity field as a result??
How come that we cannot accelerate things to v=c
yet such things can exist right now? Quite a contradiction
I'd say.
Submitted by vda"AT"port.imtp.ilyichevsk.odessa.ua 01/04
First of all, this explanation shouldn't be taken too literally! Secondly, the correct calculation is carried out within General Relativity, and hence Einstein would have been perfectly happy with it (although note that this isn't special relativity). And thirdly, there's nothing wrong with things moving apart at faster than the speed of light in an expanding Universe - it all depends on the coordinates you choose. Nothing can move relative to a neighbouring objects at v>c. And no signals can propagate between two points faster than it would take light to travel the distance. The point about inflation is that things expand apart from each other so fast that they overtake light signals passing between them. So a small "causal" patch (over which there has been enough time for light to propagate) gets blown up to gigantic size. And hence our whole observable Universe was in very good causal contact at much earlier times than you would have thought.
I'm curious about how red-shifts are used to
determine distance. I know that the greater the
red-shift, the greater the distance. But, how do we
know the exact distance to red-shift factor? Is it
part of Einstein's theories?
Submitted by aaronernestoortizlopez"AT"yahoo.com 03/04
It all depends on the cosmological model. Changing the Hubble constant (i.e. the present day expansion rate), changing the amount of dark matter and changing the amount of dark energy, will make the Universe expand differently with time. So objects at the same redshift will be at different distances in models with different values for these cosmological parameters. The equations describing this are indeed derived from Einstein's General Relativity, but in fact they're not too tricky to deal with. However, in general you have to perform integrals over redshift to estimate cosmological distances, and so you can't usually write down the redshift-distance relation in a simple expression. But if you tell me your favourite values for the cosmological parameters, then I could give you a plot of distance versus redshift. However, you also need to be careful about what you mean by distance (there are several possible definitions) in a Universe which is expanding and possibly curved!
1. Is space curvature governed by the cosmic gravitational field?
2. If this is true then does a perfectly flat universe imply a 0 cosmic =
gravitational field?
Submitted by labeleh"AT"msn.com 03/04
Yes, space curvature is governed by gravity. But it's a little more complicated than you suggest. You need to take into account pressure as well as energy density, and so different kinds of stuff contribute differently to the dynamics and the curvature.
In fact a completely empty Universe has open ("hyperbolic") curvature, despite what you might have thought! And a Universe with a total density equal to the critical density has flat geometry. This certainly doesn't mean that there's no gravitational force between things, just that space overall isn't curved.
Why is the redshifting of distant galaxies called a redshift?
What's red about it?
Submitted by joekuhn"AT"comcast.net 03/04
The wavelengths of the light emitted by distant galaxies are stretched, i.e. shifted redwards in the spectrum. We call this redshift. This is similar to the familiar Doppler effect caused by moving objects. A car moving away from you fast will have a noticeably lower pitch than a stationary car, and a car moving towards you will have a higher pitch. You get the same effect for light waves as for sound waves, but the effect only becomes big when you're moving fast relative to the speed of light, rather than the speed of sound.
In cosmology we think of this redshift not as a velocity effect, but simply as a stretching of lengths. When the photons left a high redshift galaxy all objects in the Universe were closer together than they are now, since the Universe is expanding. As the photons travelled towards us from this distant object they are stretched along with the expanding space. And so we observe all the wavelengths in the spectrum of a galaxy to be shifted redward.
why was there more matter than antimatter?
If it had been reversed -- if there had been more antimatter, so that
the universe eventually became populated only by objects composed of
antimatter -- but otherwise, just for assumption purposes, everything
else evolved the same way so that you and I could have this dialog in
an antimatter world, then would we perceive any difference? Would we
be mirror images (left-handed people would be right-handed) or some
other difference or would it all seem just the same?
Submitted by mmakover"AT"optonline.net 03/04
There is no clear answer to why the Universe is made of matter rather than half matter and half anti-matter. But it surely has to do with an asymmetry between matter and anti-matter particles at very high energies. This is something which can be probed in particle accelerators, and so we may learn something about this from experiments currently underway (such as the BaBar experiment at the Stanford Linear Accelerator Center. The way the Universe works made a definite choice between matter and anti-matter at early times, and the trick is to figure out the details of the correct theory which made the imbalance just the right size.
Hypothetically speaking, if the Universe had come out with more anti-matter than matter, then almost everything would have been no different. Anti-atoms behave just like atoms, with electromagnetic and gravitational forces operating on them in exactly the same way.
This means of course that in principle you could be made of anti-matter, and you'd never know!
Are the mass (or
equivalent) concentrations in supernovas sufficient to cause any noticeable
slowing in the rate at which we observe their light output's peaks and
decays? If so, does this appear only as a slowing or also as a red shift?
The big bang would have had an immensely larger mass/energy density than
even a supernova. If it were meaningful to imagine an outside observer
watching our big bang without moving relative to it, would that observer
see it seem to take longer than one minute for the CMB to form? [abridged]
Submitted by howard"AT"thrinberry-frog.com 03/04
The "Big Bang" isn't a localised place, but the whole Universe.
Different observers will measure different rates for time, depending on their frame of reference. This include the speed they're moving at and the gravitational field they're in, both relative to another observer. Observers in very strong gravitational fields experience strange things like strong "time dilation" compared with other observers. You get this near a black hole, since that's a localised region of high gravitational field. But you don't get this for the "Big Bang", since there's nowhere special for you to have a higher gravitational field relative to any other observer - because the Big Bang is everywhere!
The definition of "time" that we use in cosmology is actually quite precisely defined (but once you've understood that such a thing can be defined, you can forget about it!). You imagine "fundamental observers" all over the Universe, who are not moving with respect to each other except through the uniform expansion of the Universe (i.e. everyone moving awy from everyone else, so that all length scales are multiplied by one universal function of time only, with no spatial dependence). Then you imagine all of these observers sharing information and coming to an agreement about how to synchronise their watches. This "cosmic time" is well defined and is the obvious time coordinate to choose in a uniformaly expanding model of the Universe. That's what we mean in cosmology when we say "formation of the light elements happened in the first 3 minutes" or "we see the CMB anisotropies as an imprint of conditions in the Universe when it was about 400,000 years old".
I find it hard to think that it would stay at a constant temperature
because the Universe is expanding forever and getting less dense and
more cold. Is the same thing going to happen to all the galaxies around
us at a much more distant date, billions of years in the future? Will
they all disappear? How would future generations, if any exist, explain
a cold empty universe? How would they explain the big bang when all the
evidence to support it is gone?
Submitted by grojo"AT"elpn.com 04/04
The question of the future history of the Universe is a fascinating (though useless) one to think about.
In the Dark Energy dominated Universe that we appear to live in, the distant galaxies will move away from us at ever increasing rates, until eventually they disappear altogether! We end up with an "island Universe" around us, consisting only of the galaxies to which we are currently gravitationally bound, with the rest of the observable Universe getting emptier and emptier, while the stars in those galaxies slowly run out of energy.
It's true that it might be hard to convince people of the Big Bang picture if we lived in an apparently finite volume universe!
If almost all galaxies are moving away from us,
their speed in direct proportion to their distance, using general
relativity, can't one equally say that all galaxies are fixed and that
the Earth is shrinking, its speed relative to our distance? Is the Earth
shrinking?
Submitted by grojo"AT"elpn.com 04/04
No the Earth is not shrinking (I can think of several flippant comments here, but will resists the temptation!).
All the galaxies are receding from each other and not just from us. So the idea that our rulers are shrinking doesn't work.
It seems in general that the physics community, be it the
particle guys, or the solid state folks, or the astrophyscists,
are being forced to conclude that space-time is crystalline
in nature with some underlying geometry. Obviously the quantum
gravity theorists require some form of lattice, especially if its
a liquid crystal superfluid state. So my question deals with
this hypothetical superfluid. Is this the same as the black-body
radiator? And is the black body the same as dark matter? If not,
mustn't they be related? There is so much similar terminology
its hard to differentiate, like is the photon gas inside the electron
also black body? If space is crystallized light and galactic structures
occur in crystalline defect regions of the crystal, does matter then
precipitate from a fractured black body?
Submitted by zero.in"AT"verizon.net 05/04
It seems that you are a bit confused by a number of potentially related ideas. I agree that there is a great deal of confusing terminology!
Space-time may well be "quantised" at some fundamental level. And that may have a dramatic effect on our ideas of the very first instant of the Universe. But it really has no influence on the generation and subsequent behaviour of the CMB, which is really a low energy phenomenon.
As for the Dark Matter, it's probably composed of some particle which we've yet to understand in detail. But really no one has much more than a hunch about what exactly the dark matter is (other then knowing that it affects things through gravity, but little else), just as no one really has much more than a hunch about the basic structure of space-time and the origin of the entire Universe! The amazing thing though, is that we can imagine learning the answers to just these sorts of mysteries by studying the large-scale Universe (and particularly the CMB) in more detail.
How can there be anything outside the obervable universe? Wasn't
everything once right next to everything else? And since no two objects
can move away from each other at faster than the speed of light [abridged]
Submitted by johnk"AT"surreal.com 07/04
So that's where you're going wrong! Who says no two objects can't move apart faster than the speed of light? In a well defined sense, this is precisely what is happening for objects separated by more than the size of the observable Universe.
I am interested to know what u think are the most important
unsolved problems in cosmology and what difficulties with the hot big bang
model can be resolved by the inflationary problem.
Submitted by bullbull104"AT"hotmail.com 07/04
Gosh, I don't really know how to answer that!
The biggest unsolved problems in cosmology are basically: (1) where did the parameters that describe the Universe come from?; and (2) how exactly did structure form? Those are the "why" and "how" questions, which are always the hardest! You can split those into many more detailed questions, like "why is about 70 per cent of the Universe dark energy", or "when did stars first ionize the Universe and end the cosmological dark ages?" - but mostly such questions are sub-sets of those 2 basic issues.
Inflation is a very promising idea which solves some problems with the standard Big Bang picture, which people didn't realise were problems in the first place (the so-called "horizon" and "flatness" problems)! It also gives you a reason for why the Universe is expanding today other than "because it was expanding yesterday". But more importantly it gives a mechanism for generating density perturbations in a generic way. But there is no detailed "model" of inflation and no direct connection with high energy physics (string theory for example) at the moment. However, there is some hope that with better data (from CMB polarization for example) it might be possible to test whether inflation is right, and what flavour of inflation describes our Universe.
Will the CMB ever end? We're receiving the photons from basically the =
edge of our observable universe, and we have no idea what's outside of =
that. Could be lots of stuff, could be nothing. As our observable =
universe keeps increasing, is it possible one day, in some direction in =
the sky, the CMB will just stop because there's no more matter in that =
direction?
Submitted by johnk"AT"surreal.com 07/04
That would certainly be interesting! If we really saw something funny on large scales on the CMB sky, then it would likely indicate something odd about the Universe as a whole. So far the CMB is extremely isotropic (except for the effects of our local velocity) - and this is the best piece of evidence we have that the Universe is pretty much the same everywhere. We can also use the CMB to show that the Universe isn't rotating very much, and that the size of the Universe is a bunch bigger than the distance out to which we see the CMB photons.
It's always possible, of course, that we might one day see some sign of a finite Universe imprinted on the CMB. But for now (and the next millenium or so) things look pretty much as you'd expect from the hot Big Bang picture in which the hot phase happened everywhere at once in a very uniform and extremely large universe!
Since Earth has been around for a THIRD of the univere's life (a huge
chunk of time), and presumably the CMB was much stronger back then,
could the radiation effects have prevented life from forming on earth?
Maybe life couldn't exist anywhere in the universe until recently, when
the CMB died down to managable levels.
Submitted by johnk"AT"surreal.com 07/04
It might be true that it would be hard for life to form in the early Universe, since there was so much radiation around. But here we're talking about the very early Universe, and at those times there wasn't any structure in the Universe either!
Before about 300,000 years after the Big Bang, the CMB made the Universe hot enough that all the hydrogen was ionized. So the temperature was like the surface of a star, and so presumably prety hostile to life! But the variations in density hadn't collapsed enough to form galaxies, planets, etc.
When the Earth was forming (about 4.6 billion years ago) the Universe was already about 9 billion years old. In the best-fitting cosmological models the redshift at that time was about a half. That means that the temperature of the CMB was only about 1.5 times what it is today, i.e. about 4 Kelvin. So the CMB was as negligible (biologically speaking) back then as it is today.
As we know,the universe is expanding in accelerating rate.And most popular
explanation for that is "cosmological constant".But later I read that not
is so clear
with this "cosmological constant".I read that it has much bigger value,that
actually supposed to be.Then I read some alternative explanations for the
acceleration,something like "quintessence".So,is "cosmological constant"
proven fact,or is it just theory?Are alternative explanations for
acceleration possible?
Submitted by Alexander.Zlotnik"AT"cgi.com 08/04
Well, this all depends what you mean by "proven fact" - but let's not get into a discussion of the nature of proof!
The brief answer is that there is now a fairly heavy burden of evidence pointing to something like a cosmological constant, i.e. a non-zero energy density for the vacuum which is significant on large scales. The evidence is perhaps not quite conclusive yet, although this is probably coloured by the feeling that "extraordinary claims require extraordinary evidence". And by the fact that we have no clear theoretical explanation for why the vacuum should behave in this way. If the vacuum energy evolves with time, then that may be a clue as to its origin. We call such general forms of energy "dark energy" or "quintesssence".
Despite its theoretical ugliness, the evidence has been growing since around 1990, and is now strong enough that a randomly selected jury of cosmologists would undoubtedly reach a majority verdict in favour of "dark energy". However, it's still unclear whether it's proven "beyond reasonable doubt".
An accelerating Universe implies dark energy fairly directly. And features in the CMB anisotropy power spectrum also imply that the Universe has a large contribution to its overall energy density from something which is not matter. These pieces of evidence, together with some other supporting data, leave us with the only real possibility being that about 2/3 of the Universe's energy density is in a form with negative pressure, behaving like empty space with non-zero energy density. There are other possibilities that have been explored for explaining the data, but these are either unworkable or even more preposterous sounding!
If the curvature of the universe is dependent on the mass/energy
density, then would the curvature change with expansion? For example as the
light and dark matter are diluted by space, won't the mass/energy density
approach the dark energy value and make the universe more saddle shaped? If so,
does this pose a problem for a "spherical" universe with the right mix of
matter and dark energy so that it continues to expand and at some point must
"break" somehow to become flat or saddle shaped? I guess this is not about the
CMB per se, but at least it is not about a microwave oven either!
Submitted by gblouin"AT"rice.edu 09/04
It's always nice to get questions that aren't about microwave ovens!
You're entirely right that in general the curvature of space will change as the Universe evolves. In fact the exactly flat case is unstable, in the sense that the Universe tends to diverge away from being flat, and adopts an increasingly curved geometry. So if it's a little bit less than flat, then it will get more and more negatively curved, i.e. saddle-shaped, while if it's a little bit spherically then it will become more and more positively curved.
The current constraints say that the Universe is within a few per cent of being flat, and we don't know precisely how close to flat it is. But whatever that turns out to be, it's still a little bit mysterious that it's even close to flat today, since that would imply it had to be incredibly close to flat at very early times. This is sometimes called the "Flatness Problem", and the most reasonable resolution of this problem is an idea called "inflation", where at a very early time the Universe was driven to be very close to flat. Whether inflation really happened, and whether we can learn anything about its details, is one of the major motivations for planning future CMB experiments.
You wrote:
"and as far as we know [the universe] is infinite in volume"
This makes sense. But in a couple cosmology books I've been reading, they
give the volume of the universe before the big bang as 0" [abridged]
Submitted by dreeves"AT"brandeis.edu 09/04
I think those books are wrong! Or at least there's no reason to accept that as the right answer!
The correct value for the volume of the Universe before the Big Bang is "undetermined". I mean that partly we just don't know what the state of the Universe was like back then. But also that it might be fundamentally an unanswerable question, like "what's further North than the North Pole?" And also that in most cosmologists pictures of the very early Universe there's something quantum mechanical (read "fuzzy"!) going on, which makes quantities like time and volume tricky concepts!
I am so hesitant about what may be a waste of your time that I insist you
consider ignoring it as absurd and will be content with brief reply of
"yes".
---Have been trying to find a published calculation for the movement of
human speed (and directions) at same time with: earth spin and orbit, sun
orbit, movement of galaxy, further? movement.
Have been informed by Wright (UCLA) and Sandquist (SDSU) that it can be
figured with some precision using spherical trigonometry and an
astrophysical table after figuring my2 longitude and latitude. I should
have warned them that I'm a retired English professor, and thus wanted a
published result and not only my movement. They did say my question is not,
as I feared, absurd. Perhaps it is if the answer must be zero. Is the
question really "where are we and where are we going at what speed?"
Submitted by rkohler"AT"mail.sdsu.edu 11/04
It sounds like you already have partial answers from Ned Wright and Eric Sandquist. I'm not sure there's much I can add.
The general principles are fairly clear, and you can look up the relevant equations and quantities in many books or web-pages. However, perhaps you are actually asking for the detailed answer to your question of where we're moving through the Universe? I can't answer that for 2 reasons: firstly because it depends precisely on what things you want to include (which I'll come back to in a moment); and secondly because I frankly have better things to do with my time!
One nice thing about the CMB is that it gives us an "absolute rest frame" in which to talk about velocities. If you really want to calculate how fast and in what direction you are moving, you would need to include at least the following list: the Earth's spin, which depends on your position on the Earth and the direction of which depends on the time of day; the Earth's motion around the Sun, which depends on the time of year; the motion of the Sun with respect to neighbouring stars; the motion of the "local standard of rest" with respect to the Mily Way Galaxy; the motion of the Milky Way with respect to the centre of the Local Group; and the motion of the Local Group relative to the CMB. The problem is that the different terms are known with different levels of precision, and that since velocity is relative, you're free to decide that you want, for example, the velocity of A relative to C, when I might have expected you to want it relative to B.
Another problem is that you need to decide ahead of time how accurate you want your answer to be. That's because there are lots of subtle effects that I didn't list above, which may or may not be important, depending on your required accuracy. For example I can imagine corrections because of the non-circular Earth's orbit, because the Sun is also wobbling around, because of precession of the Earth's orbit, various accelerations or epicycles in the orbit of the Sun around the Galaxy, perturbations to the motion of nearby galaxies and clusters, etc. etc.
So if you really want to work this out, you need to specify exactly what question you want to answer, stick to a given level of accuracy, and then get out your astronomical almanac and calculator!
I have a question on the idea of an infinite universe. It seems to me
preferable to believe that the universe is finite in volume, probably
for symmetry reasons. If it is finite in time it should be finite in
space. The picture I have of the Big Bang is thus a ball spreading
outward at the speed of light. I think my idea is probably quite
common among laypersons. I found the idea of an infinite universe to
lack the neatness of the popular view. It suggests that an already
infinite space was sitting around waiting for time to begin.
To avoid dragging out this email too long, my basic question is this:
is the difference between an infinite universe and a finite universe
(perhaps of infinite mass) just a matter of convention. [abridged]
Submitted by bafryer@telus.net 01/05
I'm afraid that your picture is quite wrong! But don't worry, because the mistake you make is very common among people trying to understand the expanding Universe. I hope that there are some answers on this page that may help you.
But the answer to your question is that an infinite universe and a finite universe are in fact different. The way to think about a finite universe is in terms of the curvature of space. Imagine that we live on the surface of a "3-sphere" (i.e. like being on the surface of a normal "2-sphere", except with one extra dimension, which we can't really picture, although we can imagine how it works by analogy). This means our 3-dimensional Universe is curved in some other dimension that we don't live in (and is really just a mathematical convenience rather than being real in any case!). So if you go off in a straight line in any direction, you will eventually return to where you started (just like being on the surface of the Earth, except this works in all 3 dimensions). So this kind of Universe has a finite volume, but has no edge.
That's the sort of finite volume universe that we might live in, according to our best ideas for how gravity and geometry are related (i.e. the theory called General Relativity). The nice thing about it is that it contains everything in a finite amount of space (hence satisfying your idea that the Universe should be finite on some kind of aesthetic grounds), and at the same time you don't have to think about edges or what's outside it, because it's everything!
Rather than a paradigm of "the big bang occurring everywhere", do you
consider it possible that galaxies/matter are indeed expanding from a common
region of the known universe? If so, then would it be reasonable to use the
CMB dipole to postulate that the big bang expansion may have originated a
finite distance from our current neighbourhood?
Submitted by jcoldrey"AT"bigpond.net.au 01/05
Although you might expect that the "Big Bang" occurred in one place, in fact it happened everywhere! This might at first seem like a complicated idea, but once you get it, I believe that you'll realise that it is in fact an incredibly simple and appealing notion!
Try to picture an infinite Universe with the space itself expanding, and with no centre, just everything expanding from everything else. We're all at the position of the Big Bang!
This is a very strange question and probably horribly wrong, so please help
me. Did gravity and the strong and weak nuclear forces only start to exist
once matter was created, some time after the big bang? If so, then there
would be nothing holding the very early universe together. Is this
encorporated into big bang equations?
Submitted by tomwsmith88"AT"hotmail.com 02/05
I've had way stranger questions than that, never fear!
In the standard picture, one imagines that all 4 of the fundamental forces are combined into some kind of "quantum gravity" at around the "Planck time", which is about 10-43 seconds, or perhaps a little later in some ideas related to string theory! Then gravity separates from the other 3 forces, and a bit later (say at 10-35 seconds) the strong nuclear force becomes distinct from the other 2, which are then the "electroweak force", but separate much later into the weak nuclear and electromagnetic forces.
So the forces are always there, although in some more symmetric form in the earlier and earlier Universe. And these forces are included in detailed calculations of the early Universe, for example in the formation of the light elements etc.
No one of course really has a clue what happened in that very first tiny fraction of a second as we approach the Planck epoch. The "quantum gravity period" may in fact be the beginning of everything, and so the first 10-43 seconds may not even exist! But now I'm starting to get into answering a question that you didn't ask!
If the universe is expanding at an ever increasing rate, what would happen
once Hubbles constant approaches the speed of light? Could it lead to
another big bang as space itself is ripped apart?
Submitted by hswyers"AT"spa.com 06/02
Although we speak about the Universe accelerating, this actually means that Hubble's constant approaches a constant!
What is meant by acceleration is that the rate of change of the rate of change of scale factor (which determines large-scale distances) is positive, rather than negative (which would be deceleration). But Hubble's constant is the rate of change of scale factor divided by the scale factor. And in an exponentially expanding model this becomes a constant.
So the Hubble constant will get a little smaller than it is today, but only by a small factor (a few tens of per cent).
I am curious as to what would happen if the opposite sides of an object that
is 1.6x10-35m in size {planck length} started moving apart either at or
faster than the speed of light - would the new space created allow for the
creation of virtual particles and if virtual particles where created in the
resulting space, (and were moving to fast to recombine initially) would they
grow in number to a point where there own created gravity stopped the
expansion in the new space.
Submitted by hswyers"AT"spa.com 06/02
This sounds pretty similar to inflation to me!
Is there anything bigger than outer space?
Submitted by Abk2005"AT"aol.com 08/02
Two lots of outer space!
Would it be reasonable to assume we'd see the same CMB we see today if
it was the result of a sudden emergence of radiation from a gravitationally
enclosed Universe (ie velocity of EM radiation less than escape velocity
needed to escape summed emergent mass in an early universe) which opened up
after the velocity of EM radiation > escape velocity, as well as (or instead
of) emergence from an EM opaque early universe?
Submitted by ma"AT"star.ucl.ac.uk 02/05
I confess that I really don't understand what model you have in mind here!
However, the one comment I'd make is is that the crucial thing is ensuring that you generate the CMB while being in very good thermal equilibrium. This is typically quite hard to arrange in "local" or "recent" ideas for producing the photons. It is of course one of the triumphs of the standard hot Big Bang picture that if you assume the Universe was once as hot as the surface of a typical star and has been expanding since then, you naturally get a blackbody spectrum.
The universive is expanding (as evidenced by the red shift). I used to have
the image of objects moveing away from us. But in fact, space _itself_ is
expaning. Excluding the effect of local gravity, if two objects were at
relative rest with respect to each other, they would still be getting
farther apart becuase the space they are imbedded in is expanding. This is
important because it can explain why there are objects in the universe that
are expanding away from us at greater than the speed of light.
So, if two object were 1 LY apart with a 0 relative velovity 13 B years ago,
how far apart would they be now?
If we could ignore gravity, how long would a 13 billion year old meter-stick
be?
Submitted by tjax"AT"comcast.net 03/05
Thanks for helping spell things out for other readers of this page!
The answer to your first question is that if 2 objects started off that far apart at some very early time, then they'd be ginormously far apart today, well outside today's observable Universe. To work out the actual distance you'd have to be more explicit about exactly when they were 1 light year apart (since at exactly t=0 nothing is any distance apart from anything else!), and you have to be quite clear about your definition of distance (e.g. when is it measured?).
For the metre stick, it depends whether it's expanding or not. If it's an imaginary metre stick, expanding along with the rest of the Universe, then the answer is basically the same as for the previous question (depending exactly when it was defined as 1 metre of course). But if it's a self-gravitating "metre stick" (like a galaxy, for example), then it doesn't care about the fact that the rest of the Universe is expanding, and it stays 1 metre.
We amateurs are told that, when observing distant galaxies, the red
shifted spectrum, is caused by the recession velocity Doppler shifting
the radiation.
I can think of four different possible, ( at least in my mind )
mechanisms tha could cause the red shift:
1) The Doppler shift.
2) Time dilation of the transmitting atoms caused by the relative
velocity of the source relative to the observer.
3) The expansion of space-time during the transit of the radiation.
4) The light emanating from a gravitational well in relation to us,
the observer. PS: Could this well be caused by the universe being more
compact at the time of transmission?
Are these all happening, are some not, or are they different
interpretations of the one process?
Submitted by Keijo.Musto"AT"bluescopesteel.com 03/05
Good question!
The best answer is "3", the expansion of the Universe. You can think of the wavelengths getting stretched as the space they're travelling through expands.
However, you can also think of this as a Doppler shift caused by the recession velocity. This is really the same thing, and at least when the velocities are small, it's easy to interpret the cosmological redshift either way. However, when the velocities get large (i.e. at large enough distances that the recession speed isn't very small compared with the speed of light) you need to be very careful in interpretting cosmological redshift in terms of a recession speed (i.e. you start to realise that your interpretation might be different depending whose frame you're in, when you measure the speed and the distance, etc.). So except for relatively nearby objects (up to 100 Mpc say), it's best to stick with thinking of cosmological redshifts as being caused by "3" in your list, and not "1".
Effects "2" and "4" are also real effects which change the signals you might get from a distant object, but not in the same way as the cosmological redshift. Effect "2" is the effect that clocks will appear to run slow in an object at high cosmological redshift. So in a sense this is just the same thing as "3", but for frequencies rather than wavelengths. We certainly can see this effect in the timescales of some physical processes in distant objects of various sorts (supernova light curves, for example). Effect "4", the gravitational redshift, depends on how massive and compact the source is. For typical stars or galaxies the gravitational "potential well" isn't deep enough to make a very noticeable redshift - you have to be something like the surface of a neutron star in order for the redshift to be genuinely large. So for all galaxies observed in the distant Universe this gravitational redshift is quite negligible compared with the cosmological expansion effect.
When the universe was more compact, was all matter deeper in a
gravitational well, i,e, are we climbing out of that well as the
expansion progresses so that older objects are emitting light from
deeper in the well, hence a red shift?
Submitted by Keijo.Musto"AT"bluescopesteel.com 03/05
No. The Universe is not a "localised" object, but everything! It used to be denser everywhere, and has been expanding, making the photons stretch (lose energy) with time. But this cosmological redshift is caused by the expansion, rather than being a gravitational redshift effect.
In spare time, I am working on a hypothesis of contracting universe. Have you
ever thought of the universe with a centre of contraction? What would
the universe be like in its contraction phase? I would appreciate if you
could let me know your thoughts on this topic.
At present time, it is generally accepted that out universe is in the state
of accelerating expansion ("inflation"). Assuming contraction, in your view,
what would be seen in the sky as different from currently observed phenomena,
focusing in particular on distant galaxies, redshifts, CMB, and galactic
rotation velocities? What cosmological parameters could be used as the
most important indicators of contraction/expansion?
Submitted by goran.krstic"AT"trow.com 03/05
In the standard cosmological picture (the "Friedmann-Lemaitre" models) the Universe can be expanding, static or contracting. Einstein looked for a static solution, which is actually quite contrived and unstable, while it is more natural for the Universe to be expanding and contracting. But then in the 1920s Hubble discovered that the Universe is expanding, and hence all models of the dynamical behaviour of the Universe since then have focussed on having expansion today. Of course, it is possible that in the past or the future the Universe could have been contracting. But current observations generally rule these models out. Our Universe now appears to have accelerated expansion, and if that carries on forever, then obviously it will never contract (although there are some speculative models in which the Universe does eventually stop accelerating and start to contract).
It may be that you have quite a different picture in mind, and so I do not know for sure whether your ideas will be compatible with what we know about the Universe - but I'm afraid it seems pretty unlikely. A contracting Universe would manifest itself with a negative Hubble law, i.e. galaxies would be blueshifted. In fact if we lived near the epoch when the Universe was starting to contract, then we might see nearby galaxies blueshifted, while more distant galaxies (seen earlier in time because of the finite speed of light) were still redshifted. This would be pretty cool! But unfortunately it's nothing like the emprically observed Universe, which is consistent with uniform expansion, isotrpic in all directions, and currently speeding up.
You are talking about CMB as b-e-i-n-g the rest frame
of the Universe. [abridged] Mach's Principle:
Although there is no difference in the laws of physics,
the existence of such a rest frame is intimately related with a
coincidence, especially with the fact,
that the local inertial frame coincides with the
most distant galaxies.
And this coincidence is something, which has to be explained.
What do you think about this remarkable coincidence?
What is the cause of it?
Submitted by helmuthansen"AT"t-online.de 09/05
An awful lot has been written about Mach's principle, and much of it by people who are smarter than me and have thought more deeply about the nature of interia. However, it's not at all obvious that much of what has been written is terribly useful! People can't even agree on precisely what is meant by Mach's Principle, and there's even disagreement about whether Mach ever stated it!
Because of this, I'd prefer not to get into a discussion of this topic - sorry if that sounds wimpy!
But rest assured there are plenty of other places to read such discussions. When I googled "Mach's Principle" I got 38,200 hits. So presumably some of those are worth reading! I find that wikipedia is often a good place to start.
Why should the Hubble
constant be constant over distance? In other words,
why must there be a linear relationship between
velocity and distance in the universe (i.e., why did
Hubble get a straight line with a constant slope)?
Isn't it possible to have an expanding universe, and
yet have everything expand at the same rate, so that
there would be only one value observable for a red
shift of galaxies? A linear relationship between
velocity and distance must represent either 1)
serendipity, 2) a first appromixation that appears
linear but really isn't, or 3) a fundamental property
of the universe that I'm just not grasping at the
moment.
Submitted by sc02492"AT"yahoo.com 09/05
There are several different levels of answer to your question, depending on how much you've been thinking about this already - so choose your favourite from these 3!
At the simplest level, a linear velocity-distance law is the same thing as uniform expansion. This is an important concept to get straight if you're going to understand thge way the Universe expands. One way to sort this out for yourself is to draw a 2-dimensional arrangement of dots (representing galaxies in the Universe), then make a larger scale drawing (or enlargement on a photocopier or scanner). Choose one dot to represent you and measure the change in the distance between you and a bunch of other galaxies. You should see that the change in the distance is proportional to the distance, e.g. if you expanded everything by a factor of 2, then a galaxy which used to be 1 unit away is now 2 units away, so has moved 1 unit in the time it took the Universe to expand that much, whereas a galaxy that was originally 3 units away is now 6 units away and so has moved 3 units further away. So uniform expansion (i.e. all distances getting multiplied by the same factor) is Hubble's Law.
The next thing you might realise is that measuring the Hubble Law for distant galaxies gets complicated because of the light travel time. You're measuring the speed of a distant galaxy when the light left it, which is an earlier time than for a more nearby galaxy. So in fact the Hubble Law is only really an approximation for relatively nearby galaxies, where you don't have to worry too much about the effects of observing at different times.
Then you realise you've heard that the Universe is accelerating, rather than exapnding at a constant speed. This means that the rate at which the overall scale factor of the Universe is increasing, is itself increasing. So in fact you don't expect the Hubble constant to be constant at all! And since the Hubble constant is actually defined to be the rate of change of the scale factor divided by the scale factor, it turns out that "H" was larger in the past and is getting smaller (and will probably approach a constant once the "dark energy" takes over). In fact using observations of distant supernovae we can see back to the time when the Universe was decelerating and switched to accelerating as the "dark energy" started to dominate.
I read somewhere that the curvature of the universe is a curvature in a
forth spatial dimension. I have read elsewhere that general relativity
allows for curvature without the need for a forth spatial dimension.
Which, if either, is correct?
Submitted by fbaer"AT"c2i2.com 10/05
Both!
The curvature of the Universe is the curvature of space, i.e. in principle the geometry may not be flat. The easiest way to picture non-flat geometry is by analogy with a sphere, except in one higher dimension. So you think of going outwards in a straight line as being motion on the surface of the sphere. And as far as beings who live on the sphere's surface are concerned, they could go all the way round the Universe while always going in a straight line. Now you imagine that we live on a "3-sphere", rather than the more traditional "2-sphere". Mathematically speaking the "3-sphere" is curved when you embed it in a 4-dimensional space. But that extra dimension is just a mathematical convenience, which doesn't exist in the same way that the real 3-dimensional world exists.
But, you don't really need to worr about this, since the CMB anisotropies tell us that the Universe is quite close to being flat!
expansion of the universe-
1- what evidence supports this theory
2- explain the expansion of the universe
3- how are redshifts used to support the expansion theory
4- are we at the center of the universe? why or why not?
cosmic wave background-
1- whar is the cosmic weave background?
2- how is it observed?
3- provide an everday example
elemental Abundance-
1- explain the formation of elements, both light and heavy elements
2- what elements are the most common? why?
3- which of these elements are used by stars for fusion?
Evolution of stars and Galaxies-
1- how do scientists use stars and galaxies evolution to support the
big bang theory of the universe?
2- describe how stars change through time
3- describe how galaxies change through time
can you please e-mail the answers back as soon as possible? than you very
much!!
Submitted by abbie_20002003@yahoo.com 10/05
Ah, someone else hoping that I'll do their homework for them!
I think you'll find the answers to most of those questions on this very web-page! And there are zillions of other resources on the internet where you can also read about cosmology and answer those questions.
Except for "provide an everyday example" of the "cosmic wave background" - no idea about that one!
the age of the universe is 13 700 000 000 years, and the observable universe
has a radius of 46 000 000 000 lightyears. it seems that we can observe things
in part of the universe where light has not had enough time to get here.
Submitted by emission_nebula"AT"excite.com 12/05
Actually, we can't observe parts of the Universe where light hasn't had time to reach us. That's basically by definition! What we observe is the "past light cone" (a cone in the sense of a 3-dimensional representation of space-time, with time along one axis, and one of the space dimensions suppressed so that you can draw it), i.e. we see precisely those parts of the Universe from which the light is reaching us right now.
The reason that 46 billion light years is further that the age of the Universe times the speed of light (i.e. about 14 billion light years) is that the Universe is expanding. You can think of space stretching as the photons pass through it, so that the photons get further than they would in a static space.
Recent WMAP data analysis has shown two interesting features:
1)- The total density Omega_tot is slightly larger than 1(Omega_tot=
1.02)
2)- There is a loss of power in the very low multipoles of the angular
Power Spectrum(the quadrupole and octopole ), compared with the
predictions of the inflationary scenarios.
Some cosmologists, namely J-P. Luminet and J.Weeks, among others,have
used these two results as a proof of a non-trivial topology for the
Universe.How would mainstream cosmologists like you interpret these two
findings?
Submitted by georges_melki"AT"yahoo.com 12/05
That's an interesting question!
Let me first say that Luminet and Weeks are only just outside the mainstream! There are certainly some anomalies in the WMAP data that may be explained in a universe with non-trivial topology (a so-called "doughnut universe" for example). However, most cosmologists would regard this as merely a curiosity for the moment, since the evidence is not sufficiently strong that one is forced to the topology solution. There are plenty of other effects which could contribute to the lowest multipoles, including systematic effects in the data, large-angle foregrounds, and other physics reasons for having less power at the largest scales. It would definitely be cool to live in such a universe! Right now the evidence isn't very convincing, but time will tell.
As for the closed universe evidence
(i.e. total > 1), although the best value
is indeed about 1.02, the uncertainty in that value means that 1.00 is
perfectly consistent with the data.
If we take the sun as a model and trace it
back to the time when it was just beginning to form (4.7 Gyrs ago), would
we not be able to somehow point to the "centre of the universe" since we
know how long it took the first particles to get to where the sun is
today, from the big-bang point, (aaprox 9.3 Gyrs) and from the expansion
of the universe? This is all assuming the big-bang theory is correct.
Submitted by sara_behzadi"AT"hotmail.com 01/06
You appear to have a mental image of the Big Bang in which it is spatially localized rather than being everywhere, hence your phrase "from the big-bang point". This is the wrong picture I'm afraid!
The expansion of the Universe happens everywhere, with everything expanding away from everything else. All observers can think of themselves as the centre, since everyone rushes towards them when they imagine running the clock backwards. But that's true of everyone! And that includes an observer located on the Sun. In other words you can point to the place where the Big Bang happened, by simply pointing to yourself!
Unsolicited suggestion: Dark energy is sufficiently bizarre that I
wondered if the alternative explanation has ever been considered. Back
in my days at university, the red shift basis for the expanding universe
was the only explanation offered, but it occurred to me that the
observation could be explained equally by a change in Planck's constant
over time. The observations of type 1a supernovae that have anomalous
brightness for their (red shift measured) distance could equally be
explained that way. It is also not entirely unlikely if the fabric of
space is expanding or contracting since the atomic emissions that are the
basis for light spectra would be derived from changing atomic geometries
(due to spatial expansion). It may be that there are both phenomena
acting in concert: both the old red shift notion and a change in Planck.
The type 1a supernova data could be used to assign the amount of error
that would be ascribed to changes in Planck. It is a much easier notion
to swallow than "dark energy". Who knows, it may completely upset the
expanding universe theory.....
Submitted by jps@netsplash.ca 01/06
The idea that the redshift of distant objects might be explained by variations in physical constants is an old one. There are a number of tests one can do which show that cosmological redshift is consistent with the expansion of the Universe and not with other ideas which have been dreamt up. Among these are tests of how surface brightness varies with redshift, measurements of time dilation in high redshift objects, estimates of the CMB temperature at high redshift, the equality of optical redshifts compared with radio redshifts (which might have a different dependence on physical constants), and several other related investigations of the properties of objects at high redshift.
One of the main pieces of evidence for Dark Energy is that the expansion appears to be accelerating. I think you may be a little confused here about the difference between expansion and acceleration. There's no obvious way of exlaining the acceleration with varying physical constants.
And even if you were to do this somehow, there's another problem. Distant supernovae are now seen out to distances (and early enough times) where the Universe was actually decelerating. That means that any physical effect you dream up for making distant supernovae appear fainter than expected has to explain why they get (relatively) brighter again, just as predicted in the Dark Energy picture.
I am not really sure how distance is determined currently. It used to be
that the red shift was the main determinant. For certain events, (type a1
supernovae?) a uniform luminosity is expected and the relative brightness
can be used to verify the red shift data. The discrepancy between these
numbers is (as I understand it) the basis for the idea that the expansion of
the universe is accellerating. [abridged]
Submitted by jps"AT"netsplash.ca 02/06
What is measured for distant supernovae is how the apparent brightness
varies with redshift for a "standard candle". This follows a "Hubble law"
for relatively low redshifts, but deviates at high redshift, this deviation
telling us about the acceleration or deceleration of the Universe.
What we see is that distant supernovae are a bit dimmer than expected in
a decelerating universe. The data fit the "CDM"
model (dominated by Dark Energy) very well.
One can of course imagine other ways for distant supernovae to be
dimmer, e.g. evolution (i.e. the average supernova brightness being a
function of cosmic time), intervening dust absorption or variations
in fundamental physics. However, there are ways to test all of these, and
moreover you'd have to contrive that the variation would look eactly
like the CDM prediction. And this is much
harder to contrive now that we've seen back to supernovae during the epoch
when the Universe was decelerating.
It occurred to me last night that the simplest explanation of the extra red
shift assigned to dark energy would be the effect of spatial expansion on
the light as it travelled from its source to us. If we posit that the light
is affected by the expanding universe so that it too is "expanded" with the
universe, we see an effect that provides an additional red shift beyond that
from relative velocity. [abridged]
Submitted by jps"AT"netsplash.ca 02/06
This is the effect of redshift! The wavelengths of the photons get stretched on their way to us, which we can interpret in terms of a velocity of recession of the source. But it's not correct to include the effect twice.
I was wondering if you could explain to me the reason for density
fluctuations in the early universe.
I've searched for an answer but nobody seems to be very clear on the subject!
Submitted by Kirsty.Macleod"AT"newcastle.ac.uk 02/06
I don't know precisely what you mean by "reason" - I'm not sure that I understand the fundamental reason why the Universe is the way it is!
However, let me assume you were asking a question about physics rather than philosophy.
We know that the Universe today is pretty lumpy, and that "gravitational instability" means that it gets lumpier with time, and hence that it used to be pretty smooth. But you still need to have "seed" perturbations which grow into galaxies and other structures in today's Universe.
No one knows for sure what the mechanism was that produced those density perturbations in the early Universe. But by far the most attractive idea is called inflation. A period of exponential expansion at early times can explain many different things at once, and generically makes density perturbations from the quantum fluctuations of the field which dominated the Universe at that time.
Further investigation of CMB anisotropies holds the promise of being able to probe some details of the inflationary epoch, or perhaps showing that we need to consider other ideas. So there is genuine hope that we can learn more about where all the structure in the Universe came from.
The mathematical equations may say that space is
expanding, but what does it really mean to claim that
there is increasingly more space between two
relatively motionless marks? More space, yes; but with
respect what??? What is the standard by which I can
verify that two balls are separated by 1 foot Monday
morning, and by 2 feet Tuesday morning; and this
without any relative motion between them?
Submitted by cmaj10"AT"yahoo.com 04/06
Who says that there's no relative motion between them?
The idea of the expanding Universe did not come from the mathematical theory of space-time, but from the observation that distant galaxies are moving away from us. The work of Edwin Hubble in the 1920s demonstrated that the Universe is expanding, and not static, as had been assumed by everyone (including Einstein).
The proportionality between recession speed and distance which Hubble discovered is precisely what you expect to see in a uniformly expanding space. The empirical consequence of expansion is that the spectra of galaxies are redshifted, with the amount of redshift increasing with distance.
The idea of the expansion of space came from hard observational evidence. And then was immediately interpretted in terms of expanding models of the Universe.
This is certainly one aspect of cosmology which is firmly rooted in empiricism! And the evidence has only become stronger in the last 80 years.
Physicists claim that even WITHOUT motion, the amount
of space that separates a pair of galaxies increases
over time. This of course also applies to any other
pair of objects. As a physicist you must be of the
opinion that between ball A and ball B there is some
distance d Monday morning, and some distance d + delta
Tuesday morning, where delta > 0. And I'm telling you:
very fine, but please demonstrate that to me with some
apparatus and some standard, not with equations. What
will be your apparatus and standard? (Assuming that
infinite precision is achievable)
If you can't answer that question and you still hold
that the current theory is correct, I will have no
choice but to conclude that physicists are members of
a sect they can't get out of.
Submitted by cmaj10"AT"yahoo.com 04/06
Unfortunately it's impossible to carry out a table-top experiment to demonstrate the local expansion of space - for a number of reasons. Firstly, the space near us is not expanding, since we live in a gravitationally "bound" part of the Universe, or in other words, our region stopped expanding a long time ago because of its own self-gravity. Another reason is that you have to go to cosmological distances to detect the expansion, since the Hubble constant is very small by terrestrial standards. You'd have to wait the age of the Universe to see a large change in distance, and so in (say) 10 years, you'd only get a change of about one part in a billion.
But because the Universe is expanding uniformly in all directions, then more distant objects are moving apart more in any fixed time interval. This means that the apparent speed of recession grows with distance. And this is what we see as the "Hubble Law", i.e. the redshift of galaxies growing in proportion to how far away they are. This was first discovered in the 1920s, and with modern technology is pretty easy to demonstrate. There are probably thousands of telescopes round the world capabale of making the required sorts of spectroscopic measurements.
There have been several proposals (in the decades since Hubble's discovery) which attempt to explain the redshifts without cosmological expansion. But none of those have been successful, since they either fail other tests (e.g. ideas like "tired light") or they are entirely ad hoc, with no theoretical basis or predictability (like "quantised redshifts").
So we are left with the idea of cosmological expansion, which is in fact the simplest model within General Relativity. This is a well tested theory of gravity, which works so well, that we have some confidence we can apply it to the whole Universe. With the assumption that the Universe is pretty much the same in all directions and positions, we end up with GR-based cosmological models which have a single "free function" which scales all distances at each time. The Hubble constant is just related to the rate at which this function is currently changing with time. And GR tells us how this function changes, depending on the contents of the Universe. So much of cosmology is focussed on trying to determine this function, often called "a(t)", and hence what the Universe is made of and how it evolves.
It appears that the very early universe had a large number of photons of
very short wavelength perhaps as small or smaller then the planck limit
10(-35)meter. However the amount of matter (the gravitational field) of
this universe was small since at this point the universe was mostly
energy therefor why did not this early gamma ray spectrum propagate
without scattering since there was no gravitational "brake" to shift it
up in wavelength (gravitational redshift). What mechanism would be
responsible for eliminating these photons? Could they not be present but
undetectable with present means?
Submitted by vick"AT"metadigm.com 04/06
It's true that the very early Universe contained a lot of very short wavelength photons. But we can't really push the Big Bang picture back until the wavelengths were below the "Planck length", since we don't have a theory of "quantum gravity" (which is what the Planck length means).
The density of matter at that time doesn't really come into it. In fact regular "non-relativistic" matter didn't exist, since everything was so high energy, so all the particles you've ever heard of (and others too!) were all in equilibrium with the radiation.
The redshifting of the CMB is not caused by the gravitational redshift from the matter in the Universe. Rather, it's a result of the expanding space that we live in. It appears that the Universe has been expanding from very early times, and hence cooling down all the time, as the photons within it have their wavelengths stretched.
What mechanism was responsible for setting the Universe off in its early expansion is of course not known. But the idea of "inflation" has a lot of theoretical appeal, as well as some growing circumstantial evidence.
The high energy photons from the early Universe are the same photons that we see today as the CMB, redshifted by a huge factor because of the universal expansion.
Regarding the principle of equivalence, if it is true that we cannot tell
the difference between a gravitation and a uniform acceleration, could we
explain the observed apparent red-shift of distant galaxies in the
universe as a gravitational impact on their own light, rather than firmly
sticking to the current theory that the universe is expanding and that,
therefore, almost all visible galaxies are moving away from us at ever
increasing speed? In addition, would it not be reasonable to assume that
light from distant galaxies, millions of light years away from us,
undergoes significant gravitational impact, not only from its own source,
but also from numerous other gravitational fields on its way to the
observer (i.e., our planet Earth)?
Submitted by goran.kristic@trow.com 04/06
You seem to have understood some of the ideas of General Relativity, but to make more progress in understanding cosmological models, I'm afraid there's no substitute for developing a deeper understanding of GR.
The standard cosmological picture is consistent with the simple "Friedmann-Robertson-Walker metric", which comes from GR, plus assumptions (which are well confirmed observationally) of smoothness on large scales. So the expanding Universe picture is entirely consistent with GR, and GR tells us how the change in the expansion depends on the contents of the Universe. This means that the effects of gravity (at least from the average distribution of matter) are already in there - so you're not allowed to add in such effects again.
Besides which, you can calculate the gravitational redshifting effects of local lumps of matter, such as the Earth, Sun, and even Milky Way and other galaxies. Those effect are really quite negligible - you only get large gravitational redshifts when photons come close to extremely compact objects, like neutron stars or black holes.
Apparently we have no other means of knowing whether distant galaxies are
moving away from us, but to measure their redshifts. Or do we? Again assuming
that the principle of equivalence is correct, if a hypothetical distant
galaxy shows significant redshift, is it possible to distinguish between the
proportions of this redshift attributable to a.) its gravitation field and
b.) its motion away from us?
Submitted by goran.krstic"AT"trow.com 05/06
You're right that, in principle, for an individual object, there's no direct way to tell the redshift of motion from a gravitational redshift.
However, to get a genuinely large redshift (approaching one, or even larger than one), you need to be in an extremely strong gravitational field. Basically you have to be near a black hole. And the light has to originate near the black hole - it's no good having the light pass near a black hole on its way to us, since the photons just blueshift as they approach the hole and redshift as they leave, giving a net effect of zero.
If the light was coming from near a black hole, then the object itself would look very different than a "normal" galaxy. There may be black holes in the centres of galaxies, but they have negligible gravitational effect on most of the stars or the light from those stars. So it might be reasonable to imagine large gravitational redshifts from peculiar looking objects. But not for regular looking galaxies.
When quasars were first discovered in the 1960s, some people suggested that their large redshifts could be due to gravitational redshifting. However, as quasars of increasingly high redshift were discovered, this idea was abandoned as being not feasible.
It's clear that the only explanation that makes any sense for the large redshifts measured for distant galaxies is the expansion of the Universe.
I know the further away we look into space the older the
universe that we see. But is it also right that the volume
that we can see is larger?
Submitted by helmuthansen"AT"t-online.de 06/06
Actually, as we look out into space the younger the things are that we see! That's because light travels at a finite speed, and we see distant things as they were when the light left them. Hence more distant objects are seen at earlier times in the history of the Universe. The CMB, for example, gives us a snap-shot of what the Universe was like when the CMB photons last interacted strongly with matter, which turns out to have been only about 400,000 years after the Big Bang.
Another concept which might be confusing you is that of the "observable Universe". This is the region from which light can have reached us in the age of the Universe. This region is getting bigger all the time, both in terms of distance and volume, simply because the Universe is getting older.
When it is reported that the age of the universe is 13.7 +/- 0.2 billion
years or that the spectral index is 0.95 +/- 0.02 etc., should these be
intrepreted to mean that the probability that the true parameter value is in
the given (1 sig,a) interval is 68% or that 1 sigma confidence intervals
capture the true paramete value 68% of the time?
Submitted by vorleons"AT"hotmail.com 06/06
So now we're getting into the philosophy of statistics - a topic which I know incite strong feelings among some people!
The answer is that most of today's parameter estimates come from use of a "Markov Chain Monte Carlo" technique for sampling the posterior probability distribution in a mutli-dimensional parameter space. These estimates are explicitly *Bayesian*, although I imagine that one could re-express things in classical statistical language.
I hope this answers your question!
Any thoughts on this supposed proof of dark matter? Does it close the
book on it for you?
http://cosmicvariance.com/2006/08/21/dark-matter-exists/
Submitted by jkrajewski@pandemicstudios.com.au 08/06
This is regarding the press release in August 2006, where gravitational lensing and X-ray observations of the "bullet cluster" were used to argue for the existence of "dark matter" (or more explicitly, an offset between the dominant gravitational mass and the dominant gaseous mass within these interacting clusters).
The discussion on "Cosmic Variance" is quite helpful I think - so I encourage people to go and read that for more information and opinions.
My own view is that this isn't really very new, it's just a particularly nice visual example to add to the pile of evidence that there's mass out there which is "un-shiny".
I think society cannot afford cosmology
given the threat to mankind in this day and age and that universities
should employ physicists to think of ways for a better world
here and now to avoid starvation around the world not spending billions
of $$ wondering about the big bang or where the edge of the
universe is !!
P.S. Please circulate this to all your colleagues and help stamp out
cosmologists and other parasites of society and work to remove stupidity
and make science benefit mankind with useful benefits here and now !!!!
Submitted by jnz9876"AT"yahoo.co.uk 10/06
Well, that's certainly a point of view!
I suspect that whatever it is that you engage in for a living could be attacked at least as vehemently! Let me say a couple of things in defence of cosmologists though.
Firstly, the amount of money spent on cosmology is very little in comparison with many other areas of science -- it is very small indeed compared with the manned space programme, and of course pales into insignificance compared with spending on weapons etc.
So one point I always like to make is that cosmology may not be very useful, but that means it's not very harmful either!
The positive point to make though is that there are some things that it's worth some people doing just because they're cool! I would place in this category literature, art, music, cinema, history, and pure science, which includes cosmology.
If no one devoted any resources to any of those things, it's unclear that we would be much better off in terms of health, the environment or quality of life, but the world would surely be a much poorer place as a result.
Why is the expansion rate of the Universe (Hubble's constant) related to
the age of the Universe in the current cosmological model?
Submitted by mbohon"AT"comcast.net 10/06
If the Universe had always been expanding at a constant rate, then one can take Hubble's law v=H0 × d (where d is the distance) and show that any 2 objects currently separated by distance d were in the same place a time 1/H0 ago, and that this is independent of the original distance d. So that's the simple "back of the envelope" calculation.
We know that the Universe hasn't always been expanding at the same rate. In fact it was decelerating for a while, and is now accelerating. We have constraints on how the "scale factor" a(t) varies with time in the best-fitting models, in which H0 is the rate of change of a(t) measured today, and the acceleration just means the rate of change of rate of change of a(t) (conventionally divided by H02, but that's a detail). The simplest cosmological models that come out of General Relativity allow us to figure out how a(t) behaves given different contributions from matter, radiation and vacuum energy. Then we put all the constraints and models together to get an estimate of the total age, which in practice comes from a numerical integral over the function a(t). This calculation involves only the overall "scaling" of distances in the Universe, and not any specific distance between objects. It also doesn't depend on the Universe being finite in size or anything like that.
It turns out that when you do that for the current best-fitting cosmological models, then the effect of the acceleration compensates for the effect of the deceleration fairly closely, and you end up fortuitously with an age which is very close to 1/H0!
The question is basically, "How is it possible for us to still detect the CMB?"
Now, don't think that I don't understand the answers you gave, I do; but the
consequences of the answers seem unlikely. At one point you wrote, "When we
study the CMB sky we are learning about the bits of the Universe that are 13
billion light years from us, as they were 13 billion years ago," but that means
that the universe was at least 26 Giga light-years diameter only 380,000 years
after "ignition" (for want of a better word). Assuming that Hubble's constant
has always applied, that means that the universe was not much smaller than that
at time zero.
An initial universe size as suggested by your answers seems even more unlikely
than the normal belief in a singularity. In the latter case we can simply say
that we cannot understand from where all that energy suddenly erupted and what
was the initial state of matter/energy, but it is much harder to take that
position if the initial size was 20 Giga light-years across.
[abridged]
Submitted by irvin"AT"lineone.net 10/06
I'm afraid there are several misconceptions here. But the basic one is the idea that the Universe needs to be finite at all. It may be easier to think of the Universe as "very big", and we do indeed see the CMB photons coming to us today from regions which were pretty far away from us when the photons left at early times. Also remember that the Universe is expanding, so 20 billion light years physical size today is much smaller as a physical size at very early times.
Do you happen to know the denisty of the
universe at the time of last scattering?
Submitted by bicycle_physics"AT"yahoo.com 11/06
Yes I do happen to know that!
The answer depends on exactly what you mean by density (mass per unit volume or number of particles per unit volume? Dark matter? Baryons? Photons? etc.). But the basic fact is that as the Universe stretches the volume increases, so as you go back in time to higher redshift "z" the density goes up proportional to (1+z)3, with last-scattering happening at about z=1000. So if you have an estimate of the average density of something today you can easily calculate its density at z=1000.
If the Hubble Constant was
found to smaller than what we currently think it is, say to 59 (km/sec)/Mpc,
then how would the temperature of the CMB, the redshift of the last
scattering surface, and the typical angular size of patches in the WMAP map
change? Also, would our estimates of the luminosities of and distances to
distant supernova change? Would our estimates of the age, the density and
the density relative to the critical density of the Universe change?
Submitted by adam.glick"AT"starpower.net 12/06
That's a lot of different questions!
If the Hubble constant was different, then it would have no effect on the current CMB temperature or the redshift of last-scattering or even of the angular size of patches of CMB anisotropy (things would change if you have a picture in mind where you fix something else, e.g. if you set the temperature at some specific early time, or set the size of the density contribution of dark matter or something - but I'm assuming that's not what you meant).
The age of the Universe changes in inverse proportion to the Hubble constant, since 1/H0 is essentially a measure of the time back to when everything was in the same place. And the distances of all objects with a measured velocity would also change, also inversely with the Hubble constant, since that's how we estimate distance for objects which are cosmologically far.
How do the discoveries of Hubble and their implications, the big bang and
steady state, CMB, COBE, WMAP, inflation, and the today's View on the BIG
bang come together or tie together?
Submitted by lbidad"AT"yahoo.com 1/07
That's a pretty general question, so it's hard to know where to begin!
Let me try to be succinct. We learned from Hubble and co. that the Universe is expanding, and then from the evolution of radio galaxies etc. that the Universe wasn't in the so-called "Steady State", and then from the discovery of the CMB that the Universe is full of relic radiation. Putting that together, the Universe was once much hotter and denser, and that's what we call the "Big Bang picture".
The detection of CMB anisotropies by COBE and subsequent precise measurement of them by a host of experiments (including WMAP) showed that we could answer some specific questions relating to exactly what sort of Big Bang model is right - in other words we can measure the quantities that describe the contents and expansion history of the Universe. Included in that is some information about the form of "lumpiness" laid down at very early times, which subsequently grew (through gravity) into all the structure in today's Universe. And the properties of those "initial seed" density variations match closely to the predictions of the idea called Inflation, where the very early Universe underwent a period of extremely rapid expansion. We still don't know whether Inflation really happened, but we're not done measuring things accurately yet!
Since the universe may wrap-around, as you say on a 3-sphere, could it be
that when we look vast distances away like 13 billion light years,
we're actually seeing light that's already wrapped around the
whole universe a few times before? Could there be a finite amount of
matter but we see it mostly endless in every direction because it's
repeated as the light wraps-around??
Submitted by jkrajewski"AT"pandemicstudios.com.au 2/07
In principle the Universe could have been a bit like this, and the idea that you can see all the way round is certainly intriguing! But unfortunately the evidence is that the Universe has pretty close to flat geometry, i.e. there's not much curvature at all. We're very far from living in the sort of space where you could have seen all the way round in the age of the Universe.
So we live pretty much in boring old flat space, and you'll never be able to see the back of your own head by looking through a telescope!
It occurred to me that there may be an effect from the creation of quantum
black holes at the time of the formation of the universe. The observed extra
red shift may be due to a gravitational effect combined with a dimming effect
(which would make the type 1a supernovae appear further away) resulting from
a greater abundance of quantum black holes in the era of emmission of the
light from the supernovae [abridged].
Submitted by jps"AT"dccnet.com 3/07
I don't really know what a "quantum black hole" is, or how they would form and subsequently behave. However, there are some well-developed ideas involving primordial black holes - and these are strongly constrained by a variety of observations. So we know that (relatively speaking) there aren't really very many of these min-black holes around, and they can't have any dramatic effects on the propagation of light in the Universe.
How do you calculate the density and diameter of the universe at a time
that the redshift was equal to z=6.56, when the current density is
3× 10–27 kg m-3.?
What does the formula look like, if I knew what the formula looked like I
might be able to answer it.
I have looked on the web, but I have not seen any thing (what I found was
WAY over my head L ).
Submitted by Seamus.Byron"AT"lyit.ie 4/07
Sounds like someone has homework to do!
The basic principle is that the density of matter just dillutes as the volume increases in an expanding Universe. Since length scales are expanding like (1+z), and volume is length cubed, then density is simply proportional to (1+z)3. So you can calculate the density at the epoch corresponding to any observed redshift.
As for the "diameter of the Universe", that depends on precisely what the definition of that is! Probably the question is talking about the "observable Universe", but for flat space the diameter is of course infinite. See how many marks you get with that answer!
This AScribe Newswire raises serious scientific questions about the
validity of the bottom-up theory of galaxy formation. If it is invalid,
how does that affect the validity of the Cold Dark Matter theory?
Submitted by Jsdrex"AT"aol.com 5/07
There is an ongoing debate about an issue that has become known as "cosmic down-sizing", meaning that it appears to be the case that some of the biggest galaxies form earlier than many of the smaller galaxies. This appears to be counter to the "bottom-up" or "hierarchical" picture of galaxy formation. But most cosmologists consider this to be an issue which is mostly concerned with the behaviour of the "baryons", i.e. the normal matter, rather than having to do with the properties of the dark matter.
The evidence that dark matter grows lumpier with time, and is initially smoother on large scales than on small scales, is extraordinarily strong. This is what we observe in the CMB anisotropies, in galaxy clustering, gravitational lensing and many other cosmological measurements. The dark matter is very simple, since it only feels any significant effects from the force of gravity. Hence calculations are relatively easy to do (both analytically and on a computer), and they agree vwey well with what the data tell us. The baryons (i.e. atoms) on the other hand, are fiendishly complicated! They suffer pressure forces and feedback effects from stars, supernovae, black hole accretion disks and all the other astrophysical objects that form once the Universe gets very lumpy on the smallest scales. The study of precisely how these baryons behave in the evolving gravitational potential wells of the dark matter has come to be known as "gastrophysics". Calculating anything in detail for the baryons is extremely difficult, because there is so much physics to include, and you need to follow things on such a wide range of scales simultaneously.
So a summary of the current status is: the "Cold Dark Matter" picture of hierarchical build-up of galaxy halos is in very good shape, but what we don't yet understand is how the gas interacts with those halos to form galaxies of the sort that we observe over a wide range of redshifts today.
I have a question that have been troubling me for a while ,I have been reading
your question and answer page and I have not found anything to help answer my
question. for the purpose of this exercise let us agree to give the Hubble
constant a value of 71km per second per mega-par sac,let us also agree that
the recession velocity of galaxy A moving away from our observer on earth is
300,000km per sec.
the Hubble length =C/71km=4225.35 mega-par sac . And the age of the visible
universe 13.7 billion years .
The observer is a hypothetical observer his life spent is 12 billion years .my
question is:1..what is the recession,velocity of galaxy A, what is the Hubble
length of the visible universe,when the visible universe was 6.85 billion years
old .And when it was 1 billion years old .
Submitted by nickst"AT"tpg.com.au 7/07
To answer this question in detail requires a precise mathematical model for the history of the expansion of the Universe. Although this is fairly simple, because the dark matter and dark energy have different contributions as a function of time, the expression that you can write down for the expansion rate as a function of redshift contains several terms. This is usually called the Friedmann equation - it is a fundamental relationship which comes directly from General Relativity, using the assumption that the Universe is statistically the same at all positions and in all directions.
To get redshift as a function of time you have to integrate this equation, and since there are multiple terms, the integral has to be done numerically (i.e. on a computer). The precise relationship between the Hubble rate and the redshift depends on the parameters of the cosmological model (in particular how much dark matter and dark energy there is today) - so the answer depends on whether you think there's 0.7 of the critical density in dark energy, or 0.73 or whatever (as well as whether the dark energy itself evolves with time). I tell you all this just so that you appreciate there is a precise answer to the sort of question you're asking! Doing it yourself just requires a bit more mathematical rigour than I normally get involved with when I answer questions on this page. But it is doable.
To give you a specific answer though, let me focus on the times that you asked about. If the current age of the Universe is about 13.5 billion years, then the age was about half of that for objects that we observe with a redshift of around 0.8 (assuming the currently standard cosmological parameters). It turns out that the Hubble parameter was about 1.6 times larger at that epoch, i.e. around 110 km/s/Mpc. And when the age was 1 billion years, the redshift was about 5.5 and the Hubble parameter was about 17 times bigger than today.
Figuring out how fast things are receeding from us is a more tricky question, because it depends what you mean! Since the Universe is expanding, then one has to be careful to define both distance and time carefully (relative to what? in whose frame? measured when? etc.). But really this isn't important, since cosmological expansion isn't really a velocity effect anyway, it's caused by the fact that all distances (including the wavelengths of photons) in the Universe are bigger when the photons get detected than they were when those photons were emitted by a distant object. It is this "redshift" which is the observable quantity, and this has a very simple relationship with the "scale factor" of the expansion of the Universe: the scale factor is just 1/(1+redshift). So at redshift of 0.8, everything in the Universe was closer together by a factor of 1/1.8, i.e. about 0.6. And when the redshift was 5.5, everything was closer by a factor of 1/6.5 or 0.15.
I read dark energy is the 74% of the universe and that it is
opposite of gravity
then instead of atracting is repeling? could you please explain how?
because either way is atracting
Submitted by jacomiz"AT"hotmail.com 8/07
The statements about Dark Energy being "repulsive" or "the opposite of gravity", are over-simplifications. This idea kind of helps people understand the effects of Dark Energy, but only kind of! When you want a deeper understanding, then these pat explanations actually get in the way!
Dark Energy is a substance which has positive energy density, but negative pressure. This means it's unlike normal matter or even "radiation", both of which have positive pressure.
In General Relativity (the extremely successful theory for gravity, introduced by Einstein almost a century ago), mass can curve space. But actually energy also serves as a source for curving space, as does pressure - these effects all have the same sign, so Dark Energy gives positive curvature to space, just like normal matter or radiation. However, mass, energy and pressure also have an effect on the dynamics of space, and it is in these effects that the negative pressure of the Dark Energy has the opposite sign to the usual positive gravitational forces of regular stuff.
So Dark Energy has a "repulsive" or negative effect on the dynamics of space (i.e. it makes the Universe expand faster), but actually has a positive effect on the curvature of space.
This is precisely the effect that "vacuum" has in the equations of General Relativity, as introduced all that time ago. What cosmologists are now trying to understand is whether the Dark Energy is just constant vacuum energy, or whether it varies with time.
I hope this explanation helps. If you really want to get a deeper appreciation of how this all works, then I'm afraid there's no substitute for learning some General Relativity!
If dark energy is repeling all matter then it is got to be right in the
middle of the universe?
Because the universe is expandig?
Before the universe reaches its limits what is behind the limits?
Submitted by jacomiz"AT"hotmail.com 8/07
The modern picture of the Universe is that it is pretty much the same everywhere, and goes on pretty much forever in all directions. The Dark Energy is no different than the other components of the Universe in this regard - it's distributed evenly all over the Universe, and makes every bit of space expand from every other.
The notion that there's a centre to the Universe is the obvious one for many people. However, this picks out one very special place, and potentially makes all physical quantities a function of distance from that place. In fact the picure in which there are no special places and the Universe is the same everywhere is actually much simpler! Maybe a little hard to get your head round at first, but once you get used to the idea, it's incredibly appealing in its simplicity.
Do principles of General Relativity apply at the level of Big Bang? If not,
at what point since the Big Bang do the principles of General Relativity
become applicable?
Submitted by docgsb"AT"telus.net 9/07
By "the Big Bang", I assume you mean the very first instant in the history of our Universe?
We really don't know what happened at this moment. But one thing we do know is that General Relativity won't work any more. "GR" is extremely useful as a description of gravity, even (as far as we can tell) in very strong gravitational fields. But it's an "incomplete" theory, because it doesn't contain the ideas of quantum mechanics, which we know apply on the very smallest scales. So when everything was very high density in the very early Universe, then you need a more complete theory to describe things - that's usual called Quantum Gravity. There are several good ideas for what that theory might be like ("string theory" for example), but there's a long way to go before we fully understand this epoch in our history.
Is the following calculations the age of the
universe correct,if not where have I gone wrong ?
1. the formula for acceleration a=v-u/t or deceleration :
2. The formula for distance is: S=v^2-u^2/2a :
3. Substituting v-u/t for (a) we derive the equation S=v^2-u^2 /
2(v-u/t) :
4. Solving for (t) t=2s *(v-u/v^2-u2)
Where t=time in seconds s=distance in centimeters,
v=final velocity.0005 cm/s/Mps =Ho=50km/s/mps when radius is 6000Mps,
u=initial velocity cm /s/mps=Ho=300000km/s/Mps when radius is 1 Mps.
Using these formulas, let us know calculate the adjusted age of the
universe using the adjusted model
deceleration perimeters q=v-u / v^2-u^2 =.0005*10^10 - 3*10^10/
(.0005*10^10)^2 -(3*10^10)^2 = .3333777^-10 of a cm/cm/sec
The above equation states the deceleration of the Hubble constant from
300,000 km/s/Mps, after a time, (TX) when the radius of
the universe was 6000 Mps and the Hubble constant is 50 km/s/Mps.
Therefore, the time required for (one Mps) to decelerate from a Hubble
constant of 300,000 km/s/Mps, to 50 km/s/Mps.we will
use equation ( 4 ) to calculate the age of the universe,
t=2*3.08633*10^24 * .3332777*10^-10 =2.0572*10^15sec.
1 lightyear=3.15576*10^7 sec.
t= 2.0572* 10^15/ 3.15576*10^7= 6518873 years for 1Mps to decelerate from
a Hubble constant of $300,000 Kps to 50 Kms.
So the age of the universe =6.518873*10^6* 6000Mps= 39.1532*10^9 *2/3 =
26.0754*10^9 lightyears.
which is twice the age of the standard model
Submitted by nickst"AT"unwired.com.au 10/07
I'm not sure precisely what you've done here, and what assumptions you've used (e.g. where your initial velocity choice came from). But I'm pretty sure you can't really do it this way, because those formulae are only applicable if you have constant acceleration. In the Universe the expansion used to be slowing down (i.e. there was deceleration), and is now speeding up (i.e. acceleration). The correct way to estimate the age of the Universe is to take the relevant equation (called the "Friedmann equation") and integrate it from t=0 until now to see what age you get. It turns out that the different terms in the Friedmann equation (radiation, matter and cosmological constant usually), have different effects at different times - but for the best estimates of the cosmological parameters, the deceleration and acceleration almost cancel out - the resulting age of the Universe turns out to be very close to 1/H0.
[abridged]
This is my definition of the edge of the universe which you and others
say there is no edge . "the edge of the universe is a point in space and
time moving in the direction of the expansion at the speed of light .Which I
call the wave front, where there is no point past the wave front.every thing
that we know to be the universe ,gravity, fields, stars,. Is within the
edge (wave front)of the universe .
Submitted by nickst"AT"unwired.com.au 12/07
This is precisely the usual definition of the "radius of the observable Universe", which is more techinically called the "particle horizon". It's great that you came up with this concept independently!
If Dark Energy is not being "diluted" with the expansion of the universe, does
this mean that the total quantity of Dark Energy in the universe is increasing
as the universe expands?
How do we know that the CMB is being "diluted" as the universe expands?
Conversely, how do we know that Dark Energy is NOT being diluted as the universe
expands?
Submitted by chadswhite"AT"juno.com 01/08
In an expanding Universe the amount of Dark Energy per volume of space stays (very nearly) the same, while the amount of matter or radiation decreases. That means that the ratio of Dark Energy to other components is increasing with time.
As for how we know about the evolution of the components - that's part of the standard cosmological picture. One models the CMB (for example) as a fluid which behaves like pure radiation and the Dark Energy as a fluid which behaves like pure vacuum energy. Then you can relax those assumptions and try to use various kinds of data to put constraints on deviations from that behaviour. For Dark Energy, the relevant parameter is usually called "w". Current constraints place its value very close to what is expected for pure vacuum energy, and also tell us that if "w" varies, it's a pretty slow variation. There are lots of ongoing experiments designed to measure this more accurately. If it turns out that the Dark Energy doesn't behave like constant vacuum energy density, then that would be very exciting!
when we look through a telescope we see
light from stars/galaxies/whatever thats taken X light years to reach us.
The farthest we can see are objects around 13 billion light years away,
i.e. roughly the age of the universe.
Now, if 1) that light has taken 13 billion years to get to me, and 2) 13
bilion years is the approx age of the universe, and 3) Im looking at the
object as it was 13 billion years ago, not as it is now, why do I see a
galaxy and not an opaque ball of photons and other stuff? If Im looking
at something, the light from which has taken 13 billion years to get to
me, and there was only an opaque ball of radiation and stuff 13 billion
years ago, why do I see formed galaxies? Shouldnt the age of the universe
be something like: TIME LIGHT FROM OBJECT TAKES TO REACH ME + TIME TAKEN
TO FORM OBJECT IM LOOKING AT?
Submitted by andy_kovacs"AT"yahoo.co.uk 2/08
Exactly right!
The most distant galaxies are seen back at times which are about 90% of the age of the Universe ago. So if we could figure out precisely how old they are, then (in a specific cosmological model) we could estimate the age of the Universe. In fact people do precisely that! It turns out to be quite difficult to estimate ages accurately, but nevertheless you can make some progress by pursuing this line of reasoning, and it gives decent guesses for the age of the Universe.
The CMB "last scattering surface" is the opaque radiation era that you refer to. This is further and hence earlier than any galaxies that we see, and marks the furthest that we can directly observe.
There's a slight complication in terms of the ages and distances however. The reason is that in an expanding Universe you can actually see out farther than 13 billion light years! That's because space has been expanding as the light travels towards you. But it's still true that the opaque CMB epoch is much more distant than any galaxy we have ever seen.
My question concerns the Hubble expansion. At large scales, between
galaxies the Hubble expansion pushes galaxies apart. But at very small
scales, say between two atoms a meter apart, other effects dominate so no
significant expansion between the two atoms can be observed. However, is
there a force due to the Hubble expansion that pushes these two atoms
apart that cannot be observed because its magnitude is swamped out by
other forces (eg. electroweak, gravitational) that have larger
magnitudes?
Submitted by nja15volo"AT"hotmail.com 3/08
The best way to understand this is to realise that the lumpiness of the Universe grows with time. At some sufficiently early time the space occupied by any currently dense part of the Universe (our Galaxy, the Earth, those 2 atoms you are picturing, for example) was expanding. But the density was a little higher than the average, and so that region expanded a little slower an average region of the same size. Eventually (if it is dense enough) it stopped expanding altogether, then started to collapse together as a self-gravitating object, and then forces other than gravity took over (the details are probably comlplicated!) and it formed into some stable object (a galaxy, star cluster, etc.).
So there is currently no expansion acting on objects which are self-gravitating. There was expansion a long time ago, but this region of the Universe was dense enough to break away from the expansion.
Dude, what a cop out!
"The Universe was *not* smaller in the past"????
How can that be if, on your page you say: "As space expands, the volume
of the universe increases, and we know that matter density dilutes
inversely proportionate to volume. That is, as the volume goes up by a
factor of eight, the matter density becomes one-eighth of what it
previously was."
How can the Universe have expanded, yet not have been smaller in the
past?
Submitted by andy_kovacs"AT"yahoo.co.uk 03/08
The simplest picture of the Universe is that it is infinite in size, and expanding. So it has always been bigger than any size you can think of, it's just that everything used to be closer together!
Could you, kindly, give me a concise theoretical physics definition of
'space'?
Submitted by docgsb"AT"telus.net 03/08
That's a good question! Alhough it's partly a philosophical, rather than physical one.
In a sense the answer is that since our best model for the Universe on large scales is General Relativity, then the answer is that space is precisely what it means in General Relativity.
I notice there's also a wikipedia page on this which might be helpful.
I've read over your FAQ pages about Cosmology and I never saw the
answer to the following. I've heard people say that the space between
galaxies is expanding (fact) and others that say all the stuff in the
universe could just be expanding too at the same rate and we just can't
tell (ie. a meter stick is continuously growing, but everything else with
it so we don't notice). Upon further investigation, I found that gravity
wins out over the expansion of the universe itself on small scales, so
this isn't the case. My question though is about the reverse situation.
Is it possible to assume that the space between galaxies is NOT expanding
and instead all the stuff in the universe is shrinking so that it APPEARS
the distances are increasing between galaxies?
Submitted by j_macinnis70"AT"hotmail.com 03/08
If this is a philosophical question, then of course it isn't possible to say whether all gravitationally stable objects are in fact shrinking, or indeed whether we are all just the dream of a butterfly or a computer simulation or whetever. But if this is a physics question, then one can certainly answer it in the negative. We have a self-consistent theory for describing the whole Universe, and in that theory (uniform curvature models within General Relativity) there's a scale factor which has evolution determined by the contents of the matter and energy within the Universe. That scale factor becomes stable within the region of self-gravitating objects, but expands (and is now accelerating) between distant parts of the Universe.
By reading the literature on the CMB, I've come across the sentence
"Galaxies and large-scale structure grew gravitationally from tiny,
nearly
scale-invariant adiabatic Gaussian fluctuations". Would you explain what the
term scale-invariant adiabatic Gaussian fluctuations mean? I do not
really understand what is so adiabatic about this case.
Submitted by nja15volo"AT"hotmail.com 03/08
Let me try to explain what that phrase is all about, since each of the words has a quite explicit meaning.
Firstly, "tiny" in this context is referring to the amplitude of the fluctuations rather than the physical size, i.e. they start off as very low contrast variations in density.
"Scale-invariant" is referring to how the amplitude of these fluctuations is different for different physical scales. The mechanism which made the fluctuations in the first place could have made stronger or weaker amplitude density variations towards bigger or smaller scales. "Scale invariant" means that the variations in the gravitational potential (which is related to the density variations) does not vary with scale at all. This is in some ways the simplest kind of scale-dependence you could think of - no scale-dependence at all!
The word "adiabatic" usually means that the entropy is unchanged. In this context it means that the entropy per particle does not change for each species of particle - this translates to meaning that the photons and the matter are perturbed together, with the same sign. So an overdensity in radiation is also an overdensity in matter. This only makes sense if you realise that there are alternative ways that you could set up a perturbations, e.g. you could perturb the radiation and the matter with opposite signs, so that the total density (and hence curvature of space) is unchanged - these are called "isocurvature" perturbations, and are quite disfavoured by the CMB data.
Finally "Gaussian" refers to the statistics of the perturbations, i.e. the description of the "randomness" of the specific variations in density that were "chosen" in our observable patch. "Gaussian" is the most random you can get, meaning that there are no correlations among the densities. So basically if I choose the density in one place it doesn't affect the densities elsewhere - they are all uncorrelated random numbers.
Current Cosmological convention indicates that the Universe as we know it is
expanding. One of the problems with this concept is that Newtonian physics is
limited in explaining some observations in space. For example, the outer arms
of the Milky Way appear to be moving faster than the inner sector.
Has any research been done regarding the plausibility that the Universe is
receeding, from our point of view, as opposed to expanding?
Submitted by jmar55"AT"yahoo.com 04/08
I think this is quite a perceptive question!
Although we talk about an "expanding Universe", what we really mean is that the space between objects is getting bigger, while the objects themselves (which are dominated by their own gravity) are not expanding.
Hence a "receeding Universe" is probably more accurate in fact.
While reading through your e-mailed questions before writing to you
(to assure my question wasn't already answered) I came across a question
which I feel I could assist you in answering. The question was:
"At what distance between points would space expand faster than the speed
of light?"
I figured this out for myself recently using the basic assumption that
the Hubble constant is 7% per billion years (the Hubble constant being
the rate of expansion of the universe.) This is now a simple math
problem, we then need to figure out 7% of what distance is equal to 1
billion light years (which is the distance light would travel in a
billion years.) Which gives us this equation: 0.07x = 1 billion light
years. We simply use algebra to divide the 0.07 from 1 billion light
years and get that the distance x is approximately equal to 14.29 billion
light years. So the growth or stretch of space between any distance that
is greater than 14.29 billion light years is more than 1 billion light
years per billion years, making it grow "faster" than the speed of light.
Submitted by jeffakkerman"AT"yahoo.com 07/08
This is a useful calculation. But unfortunately things are actually a bit more complicated than this, because space has been expanding, and you're looking along the "past light cone" (i.e. you see distant thingsd as they *were*, not as they "are"). So you have to be very careful to define what you mean by speed before you talk about this. The calculation you did is correct for a completely linear Hubble expansion law in a Universe where you can observe things instantaneously. But the question isn't even well-posed until you very explictly define what space and time coordinates you are using.
It turns out that when you do this, defining the most obvious set of coordinates, then you find that you can in fact observe regions which are moving away from us faster than the speed of light!
I have two questions for you which are concerned with the claim that space
around the galaxies does not expand like the rest of the universe. If this is
true then it appears to me that the redshift of the CMB would differ in
accordance with how many galaxies the radiation passes through in a given
direction. This would mean that the presence of the galaxies (including space
that has not expanded like the rest of the uiverse) in themselves would cause an
anisotropi in the CMB, as the redshift should be less when passing through
un-expanded or lesser-expanded areas of space. I don't know how large this
effect could be, but can you tell me if this effect has been considered and
accounted for in the COBE results? George Smoot does not mention it.
The non-expansion of the space around the galaxies seems to me like an ugly ad
hoc concept. Do you know of any book that explains it, or can you explain it?
Submitted by carl"AT"ullerup.com 07/08
You are partly correct, and this is very good thinking! You can think of galaxies as being "potential wells" of matter, i.e. places where the gravitational potential is lower. As CMB photons go near to a galaxy they traverse this potential well, gaining energy as they fall in and losing energy as they climb out. These energy changes would manifest themselves as what are called "gravitational redshifts/blueshifts". However, if CMB photons go right past a galaxy then the redshift and blueshift will almost exactly cancel out - hence the net effect is zero.
Still, this is essentially the physics which leads to anisotropies on large scales in the CMB. We are seeing photons scattering from potential wells and potential hills on the "last scattering surface". In other words we (the observer) are situated at a different garvitational potential than the fluctuating density field on the CMB sky, hence we see gravitational redshifts and blueshifts as temeprature anisotropies.
In addition, on large scales at relatively recent times the gravitational potentials evolve with time (because of the dominance of Dark Energy). This means that the redshifts and blueshifts don't exactly cancel out, and this gives additional effects on large angular scales. This correlates with the positions of large scale structures on the sky, and this correlation has indeed been seen (albeit at a fairly low level) in comparisons between CMB data and galaxy data. It's usually referred to technically as the "Integrated Sachs-Wolfe effect".
The general concepts of the universe, the Big Bang occuring everywhere
and nowhere, the universe being "all there is", the universe being
infinite but infinitely smaller before it got infinitely bigger with
expansion, appear to tax the comprehension of mere mortals. Dark matter,
dark energy, inflation and non-baryonic matter (96% of the universe) are
expansion, appear to tax the comprehension of mere mortals. Dark matter,
dark energy, inflation and non-baryonic matter (96% of the universe) are
all still undetected, unproven or unexplained. Doesn't it seem at least
likely that the Standard Big Bang paradigm may in fact be incorrect?
Submitted by haynes"AT"snip.net 08/08
If you have a new idea which is simpler, then I'm sure people would like to hear it!
But really, most of the current cosmological picture is fairly straightforward. It's just about the simplest model you can think of. The Universe is pretty much the same everywhere, has no curvature to speak of and is full of lumps that get lumpier through gravity. Anything else surely seems much more complicated.
Of course understanding ideas like "the Big Bang happening everywhere at once" isn't easy. But who said understanding the whole Universe would be trivial? To take a mundane example, it requires a great deal of study to figure out how a bicycle really works - so it would take a considerable amount of time to engineer an improved bicycle. And there's no obvious reason to expect it to be easier to come to grips with the structure of space and time than it is to understand some everyday object.
It is possible to reach a good understanding of the current cosmological picture - however I would claim that this isn't really possible to do at a deep level without a lot of studying. I genuinely believe that most human beings are capable of this, but it would just take a lot more time than they're probably prepared to put into it. On the other hand, most of the basic concepts are pretty easy to grasp, provided that you keep a clear head and avoid some of the common misconceptions.
I would put into that category most of the points you raised in your question. Many of them are in fact best understood by realising that the alternative is more complicated!
As for Dark Matter and Dark Energy - I take exception to statements that they are "undetected". We've very clearly seen the gravitational effects of Dark Matter, in many different ways. And Dark Energy also has to be there because of observations that we make, which require the existence of a substance which doesn't really clump and doesn't change with time. We'd really like to figure out precisely what Dark Matter and Dark Energy are, i.e. we'd like to place them within the context of some particle physics picture. But that's very different from saying that we haven't detected their existence.
But it's also true that cosmologists have been looking for alternatives. For example a different theory of gravity, which might do away with the need for Dark Energy. However, all of the ideas so far considered either patently fail the observational tests, or are very much more complicated or contrived (or both).
And as I said at the beginning, there would be a lot of interest in any new idea which seems to work and have the appeal of simplicity.
Scientist say that the universe is "flat" meaning that it is close in density
to the critical density. However, as the universe expands, shouldn't the
universe become less dense? If so, does that mean that billions of years from
now the universe will no longer be flat?
Submitted by chadswhite"AT"juno.com 10/08
The critical density also changes with time. It turns out that if the Universe is precisely flat, then it stays flat forever. However, this is an unstable evolution, meaning that if space is slightly curved, then it will evolve further and further from being flat. This can all be understood from the equations which govern the dynamics of the Universe and the curvature of space (derived from General Relativity) - but there's probably nothing to be gained by writing down the equations here (you can look up these "Friedmann equations" if you're really interested).
The fact that "flatness" is unstable is sometimes called The Flatness Problem, and is one of the cosmological issues which could be solved by inflation. The "problem" to explain is why the Universe appears close to flat today if the natural thing is for evolution to take us away from flatness. T can only mean that the Universe must have been extraordinarily close to flat in its early phases - which is something inflation could explain.
Have estimates been made for Einstein's constant? If so, what is the
estimated value of the cosmological constant?
Submitted by chadswhite"AT"juno.com 10/08
The "Cosmological Constant" is just another way
of talking about the density of the Dark Energy. In probably the simplest
units it's estimated value (from a combination of CMB data, distant
supernovae etc.) is about 70 per cent of the critical density.
Is space an absolute
quantity existing regardless of the matter that occupies it or does the
farthest cosmological object from us define the edge of the
universe? and if space was only defined in terms of the matter in the
universe, when the universe expands then "more space" is created with its
vacuum energy, from where does this energy come? I just cannot visualize
how space is treated in standard cosmology.
Submitted by T.Elsayed"AT"ThPhys.Uni-Heidelberg.de 12/08
Space exists regardless of matter. Except for the complication that matter (and other forms of energy) bends space, giving it curvature, so that if there was enough stuff in the Universe it would be closed round on itself and so finite in volume.
But the best current evidence says that the geometry of the Universe is close to flat (i.e. not very curved on large scales), and so the best guess for the volume of space is that it's infinite. The furthest even further away
If I define the Big Band as a 'object' having approximately the same size
as we see today, not counting in any expansion, then it seems to me that
I say that there will be a possibility of a object ('non spacetime')
existing before photons, particles, mass?
Submitted by yor_on"AT"hotmail.com 3/09
You appear to have a different picture of the earliest phases of the Universe than mine. I think that no one knows what conditions were like at the moment of the Big Bang. But it is probably the case that there was really no "first instant", and that time itself had a kind of fuzziness.
However, we do have a pretty clear idea of what things were like mere moments after the Big Bang. At that time the Universe was very large and hot, with everything expanding from everything else. It was filled with very high energy particles, including photons as well as massive particles.
It is not possible to see anything which existed before this. The CMB photons we observe are coming from the time when the photons last strongly interacted with the matter, which was a few hundred thousand years after the Big Bang. However, if we were able to detect primordial gravitational waves, then these would be a direct probe of these very early times. Hence there is currently a lot of excitement about this possibility in the future.
Since we understand that as we look out further and further into space it is
the same as looking back in time. Yet the nearer to the origin of time
(further out in space) the larger the universe is.
It is as if the nearer we observe the origin of the universe the larger it is.
Its almost a contradiction that the further back in time is observed the
larger it is.
Even though there was a large bang and smaller universe in the past not
larger. My question is ; Is this the reason someone had to cook up an idea
like inflation?
Submitted by m.favro"AT"sympatico.ca 4/09
I think you almost have the right picture here.
Except I'd say that the Universe was (probably) infinitely big at all times! Things were closer together in the past (because we know the Universe has been expanding) - but that doesn't mean that the total volume was smaller.
As we look out in distance we are looking back in time, and the enclosed volume gets bigger as we look further away. Eventually we see back to t=0 (or very close to it), and the total observable volume is finite. This accessible region is usually called the "Observable Universe". It is finite in volume, but that isn't the volume of the whole Universe.
This is related to why inflation was first conceived of (although the connections are a bit indirect). One part of the argument is that in the normal picture there's no reason why one side of the CMB sky should be anything like the same temperature as the other (simply because the region across which light can have travelled gets bigger with time, and we're only able to see both opposite sides of the CMB sky today). That can be explained by having a once very small patch (smaller than the speed of light times the age of the Universe at that time) expand arbitrarily fast for a while, and hence even our Observable Universe today is only a small fraction of the patch which inflated. And that patch need not be the whole Universe either!
Rephrased Question;
1.We only see light from things in space(visible universe).
Space itself (universe, whatever) is never seen and it is not what I refer to
in my question.
2. Why is it that as we look back to time zero t=0 the universe is at its
largest size - when other physicists are telling us it started with all stuff at
one point in the beginning of the visible universe.
3. Further to this contradiction that speck of light I just started its journey
towards me many billions of years ago. So I can deduce that the origin has now
moved on at near the speed of light and is actually much further away than the
visible universe as we are now observing.
4. My original Question recognized all these things and the contradiction of
further back in time things are larger not smaller as would be true in a big
bang event.
[abridged]
Submitted by m.favro"AT"sympatico.ca 6/09
I think you are very close to having the correct idea, but just need to hone a few of the details!
Although it may seem like "other physicists are telling us it started with all stuff at one point in the beginning", I don't think this is what any (sensible) physicist is telling you! The standard mological picture has the Universe being very large even at very early times. It's expanding, so objects are getting further apart, but that doesn't mean the overall size of the Universe was smaller in the past - it has always been big!
The "beginning" isn't a point, so you don't see it in one particular direction, you see it in every direction - or in other words, you can see back to very early times in the history of the Universe in whichever direction you choose to look.
I am asking a hypothetical question : observer (B) in galaxy (B)
with the Hubble space telescope.can observe the most distant galaxy(A)10 Gly
in (B) past light cone
.observer (A ) is living on the most distant galaxy(A)
1:what is the temperature measurement of (A) CBGRadiation,can
(B)verify (A)measurement.
2: what are the similarities or deference's of galaxy (A) and (B)
rate of supernova explosions,and star populations
3:what is (A) Hubble parameters
Submitted by nickAT"tpg.com.au 6/09
Galaxy A will observe Galaxy B in its distant past. Similarly, Galaxy B will observe Galaxy A in its distant past. At these much earlier times the CMB temperature would have been much higher (and the galaxies would probably have been in the early stages of their formation and evolution).
We can in fact test this by using information from the spectra of distant galaxies to put limits on the CMB temperature that is present at these early epochs (which is what observers at those times would observe). The answers are indeed that the CMB temperature was higher in the past, just as you expect in an expanding Universe.
The Hubble parameter is higher in the past. That is essentially what is measured using the brightness of distant supernovae.
If the Hubble parameter is a time variable at deferent epoch in the evolution
of the universe. as it is stated by cosmologists.
Galaxy A 10 GYs in the past light cone of our Observer with his HST, must
have a deferent expansion rate to the Observer on the HST.
For this exercise lat as give this Galaxy A at this early epoch in the
evolution of the universe an expansion rate of a 100Km/s/Mpc^-1
galaxy A emits a photon the wavelength of the photon increases as it travels
through deferent expansion rate of unit space time at each deferent epoch in
the evolution of the universe. To our Observer on the HST.
My Question :Our Observer with his HST,is hi measuring the proper value of the
expansion rate ,orthe average value of the expansion rate
Submitted by nickAT"tpg.com.au 9/09
That observer would measure the same Hubble parameter as us if you're assuming that they are making their observations at the same time as us. On the other hand, if you're asking about an observer that we can see in the past (i.e. "on our light-cone"), then they would observe the Hubble parameter that we would have observed at that epoch.
Now you're asking detailed enough questions, that you should probably find an introductory cosmology book and learn some of the real stuff, so you can do the calculations yourself!
Since the universe is expanding, then the matter in it was ever denser going
back into the past, approaching infinite density at the big bang. Surely
this means that at some point in time all the matter was within its own
Schwarzchild radius and was therefore a black hole? If so, then how did we
and the CMB get out? Or are we and the CMB still inside a black hole since
not even light can escape from one, according to Einstein's GR?
Submitted by edmund.wood"AT"wellbalanceduniverse.com 9/09
This is a very good question!
A "black hole" is a particular solution to Einstein's Field Equations, specifically for a point mass in a flat background space. The solution is quite simple because it is spherically symmetric and static (i.e. doesn't change in time). The resulting bending of space-time gives a "Schwarzschild radius" or "event horizon", inside of which nothing can get out, and this leads to all the familiar properties of a black hole (when I say "familiar", I mean from reading articles about black holes, rather than personal experience of course!).
There's a whole other class of solutions to Einstein's equations, those being relevant for describing the Universe as a whole. These solutions (usually called the "Friedmann-Robertson-Walker" space-times) are in a sense even simpler than the Schwarzschild solution, since they don't depend on position at all - the Universe is filled uniformly with matter and radiation, has curvature the same everywhere, and is expanding the same in every direction. These solutions are completely different from those that give you a black hole. And hence the early Universe was not inside its own Schwarzschild radius (because it didn't have one). There's a different kind of "horizon" in these models, sometimes called a "particle horizon", which defines the region that you already know about ("past horizon") or can ever know about ("future horizon"). So there are some analogies with black holes - but only some. The situations are really not the same at all. Black holes don't expand for one thing!
a super nova explodes at the epoch
when the universe was 3 Gy old,.the photons from the explosion spreads out as
the universe evolves to its present age.The expansion parameter varies with
time .the Observer in the present epoch makes a measurement of the red
shifted photons. And Z=1.8 the Hubble parameter works out to 71
Km/sec/Mps^-1 according to Hyper Physics***Astrophysics calculator. Which
implies that the expansion rate for every Mpc all the way back to the super
nova explosion is a constant 71Km/sec/Mpc^-1.but the statement (H)varies with
time implies that the Hubble parameter is not constant Question : is the Hubble
parameter of 71 Km the average expansion rate.
Submitted by nickst"AT"tpg.com.au 9/09
Supernovae can be used to estimate the value of the Hubble parameter today, as well as the changing acceleration and deceleration in the past.
Relatively nearby supernovae (on a cosmological scale at least!) can tell is H0 directly, if we assume they are "standard candles". Modern values come out somewhere around 71 (in units of km/s/Mpc).
Observations of distant supernovae do not give us a direct measurement of the Hubble parameter at the epoch of emission of the supernova light, or of the average epansion rate during that time. What is measured fairly directly is the "luminosity distance" out to the supernova. This is effectively an integral over the Hubble rate.
You're asking a relatively technical question here! So if you really want to know the full-blown answer, then you can look up the complete expression in any graduate level textbook on cosmology. However, you'll need to understand some background information in order to appreciate what all the symbols mean, and how they should be interpretted.
as I understand it, the Universe was initially half and half matter
and antimatter and underwent a massive annihilation phase. This would have
produced copious amounts of gamma rays. If we knew where to look, would we see
a red-shifted gamma ray background similar to the CMBR?
Submitted by soule1061"AT"verizon.net 10/09
You're correct that the simplest picture of the early Universe would be that it comes from pure energy, and hence has half matter and half anti-matter. But then the Universe today would still have a 50/50 split, and that's certainly not the case. So for some reason the early Universe (i.e. high energy particle physics) favoured matter over anti-matter. Exactly how this happened isn't known (it's called "baryosynthesis" sometimes), but it certainly gives us a clue about physics at the highest energies. It's neat that just the simple observation that you haven't annihilated with anything recently is actually a useful constraint on high energy physics!
Do you think that we will ever, if possible, have definitive proof that
Inflation, in fact, occured? And exactly what would constitute proof of
Inflation?
Submitted by andyarct"AT"yahoo.com 1/10
That's a tricky question! What exactly do you mean by the word "proof"?
Inflation has a number of generic predictions and some detailed predictions which depend on which specific inflationary model describes the Universe. The generic predictions are all basically confirmed. Except that many people would point out that they are really "post-dictions", because they were the things that inflation was invented to explain in the first place! So inflation "explains" why the Universe is expanding, has close to flat geometry, has structures of roughly the right amplitude, and has structures at scales which are apparently bigger than the causal length scale at early times.
For many practising cosmologists there are no sensible models which explain all those things and which aren't just some flavour of inflation. So from that perspective we already know that the Universe looks like it inflated, and now all that's left is to figure out what it did in more detail. However, for many other people this isn't very satisfactory, and they'd rather have something that seems more like a testable prediction, in the conventional sense of comparing a scientific hypothesis with data.
Inflation also predicts a gravitational wave component in the Universe, but of an unknown strength.
Perhaps the closest thing to a clearly testable prediction is the so-called "consistency" relation between the strength of the gravitational wave signal and its variation with scale. This will be a hard measurement to make, but may be feasible if the signal is strong enough. This is precisely the sort of thing that is being discussed for future CMB experiments.
Do you think that dark matter is actually some exotic form of matter that we
can't see, or is it more likely that we just don't fully understand how gravity
works on large scales. I tend to believe the latter; we know that General
Relativity "breaks down" at singularities, so it seems entirely possible (to me
anyway) that it fails on some level at very large scales as well. In other
words, maybe the mathematics need some adjustments. I suppose it could be a
combination of the two as well.
Submitted by andyarct"AT"yahoo.com 1/10
You're right that there are 2 basic explanations for the evidence relating to dark matter. One is that there's a kind of matter which has no electromagnetic interactions and only very weak interactions except through gravity. The other is that gravity is modified on large scales.
There have been many attempts to try to understand how modifications to General Relativity might explain what we see without the need for invoking a new form of matter. However, there are observations to explain over a range of scales, and this has proved to be difficult for any of the ideas which people have come up with. Meanwhile the Dark Matter hypothesis can successfully explain the entire range of observations.
It may be a matter of taste whether one regards modifying the theory of gravity or inventing a new kind of matter as being more speculative. But the fact is that the Dark Matter idea appears to work!
Spacetime even though now presumed to be flat will still not be so, due
to CBR?
How exactly would that be, because light (CBR) bends it?
Submitted by yor_on"AT"live.se 4/10
Universes which are close to being flat tend to get flatter during exponential expansion. In the simplest model that we have the Universe is now becoming dominated by the Dark Energy, and so the effect of the CMB becomes less and less relevant as time goes on. The Universe appears to have close to flat geometry today, and that seems likely to continue for an extremely long time!
And what is your take on the discovery that quasars don't show any time
dilation ?
Can you see a simple explanation for it?
Submitted by yor_on"AT"live.se 4/10
This is a result from one specific new study. My guess is that it might be telling us something about how quasars evolve over cosmic epochs. We certainly know that they do, because the main era of quasar activity was long in the past (corresponding to redshifts around 2), with very few powerful active galactic nuceli (AGN) existing in the Universe today. Hence we know that the average AGN billions of years ago is quite different from the average AGN today. So it's unsurprising that the variability of quasars (a poorly understood phenomenon) changes with time. And there's no reason to think that means the Universe isn't expanding!
It's hard to understand how you could have redshift without having time dilation. But I guess that in principle our whole picture (General Relativity etc. etc.) could be completely wrong, so it is always good to perform consistency checks. We certainly know that distant supernovae appear to last longer than local supernovae do, and this is completely consistent with what we expect in an expanding Universe.
what i really don't understand though, I'm fibbing of
course:) there's a lot of things I don't understand, is how expansion so
magically would be localized outside the galaxies. Even if we assume that
gravity is the 'thingie' keeping expansion away, we then seems to be
looking at matter, but not space and what keeps heavenly bodies close to
each other. So, assuming that space is space, well sort of, classically
looking that is. How can we say that there are no expansion inside the
galaxies? [abridged]
Submitted by yor_on"AT"live.se 4/10
A useful way to think about this is to realise that the formation of structure is fighting against expansion. Every region of the Universe was once in expansion, but the over-dense regions were expanding just a bit slower at early times, then later had enough excess density for their gravity to halt the expansion altogether. After that a bunch of complicated physics stops the region collapsing completely, and instead it turns into a galaxy. So the point is that the matter making up a galaxy was once expanding, but at some point in the past "turned around" and became a self-gravitating object, no longer caring that the space between it and the neighbouring galaxies was still expanding.
In all popular accounts on Cosmology, we are told that, when Einstein
introduced his cosmological constant lambda in 1917, it was because he
believed the Universe to be static. The effect of gravity would have caused
the Universe to collapse, hence the introduction of a repulsive cosmological
constant to prevent this from happening. Then, in 1928, when Edwin Hubble
discovered the recession of galaxies , Einstein withdrew the cosmological
constant, calling it "his greatest blunder". But how was Einstein convinced
that the Universe could expand under the effect of gravity alone? Recall
that in 1928, the Big Bang theory had not been invented yet: this had to
wait for the work first of of Friedmann, then of Lemaitre and finally of
Gamow, some 30 years later...
Submitted by georges_melki"AT"yahoo.com 7/10
That's a good question. And I'm not sure I can really tell you what Einstein and other physicists and astronomers were thinking back then!
Let me take a stab (with hindsight) though. In the simplest cosmological solutions to General Relativity it's "obvious" that the Universe should be either expanding or contracting. The static case is hard to arrange, and not stable. It was of course even more obvious once Hubble discovered empirically that everything is expanding. After that, the simplest picture was just that there was "regular stuff" (i.e. matter and radiation) in the Universe, and so it was expected to be decelerating. This was hard to measure, and so it is only much more recently that we discovered that the Universe is in fact accelerating.
It's true that the "Big Bang" model didn't come till later than this period. But that's because it's really the "Hot Big Bang" model - it was hotter in the past, as well as everything being closer together. The general "Friedmann-Lemaitre" models were around before 1920, they just didn't necessarily have a significant radiation content (which dominates at early times). And we didn't know that that was the case until we discoved the CMB in the 1960s.
According To Hubble's law the galaxies which are twice away from us are
moving
with twice the recessional velocity.....and 3 times away from us are moving
with still higher recessional velocity....
So ultimately will it violate the postulate of special theory of
relativity which says that the the highest velocity that can be achieved
is the velocity of light?
Submitted by sreerajt90"AT"gmail.com 9/10
Yes, there *are* galaxies that are moving away from us faster than the speed of light. But no, that doesn't violate Special Relativity. Things can seem a bit complicated in an expanding Universe, but remember that the usual cosmological picture is derived from Einstein's theory of gravity, which contains Special Relativity - so really it's not possible for there to be a contradiction.
Information can't travel faster than the speed of light. The fact that some distant galaxy is moving away from us at an arbitrarily high speed doesn't change the fact that the light leaving the galaxy travels towards us at the speed of light. If we see light from a distant that now is moving at some speed v>c then we'll never be able to send a signal back to it - it has gone!
How can we be sure the CMB represents only our universe and not the other
universes as well as ours?
Submitted by hwvolberg@yahoo.com 1/11
Normally we consider "the Universe" to mean the "observable Universe", i.e. the volume from which light can have reached us through cosmic history. Since that timescale is finite (about 13.5 billion years), and the speed of light is also finite (300,000 kilometres per second), then the distance is a finite number. We can only see effects on the CMB that come from within this volume, since no physical effect can travel faster than the speed of light.
I have read that to measure cosmic time we need to refer to the clocks of
"fundamental observers", whose relative motion can be fully accounted for by
the hubble flow (i.e. no peculiar motion). Even though these observers are
moving, we can use general relativity to show that their clocks will agree.
Therefore, it seems that not all relative motion is subject to the Lorentz
transformation, only motion in excess of the hubble flow -- am I correct? It
seems that the hubble velocity vs. distance relationship sets the standard
for what is in motion and what is at rest since only motions in excess of
this relationship should affect clock rates. Without expansion, then
commoving observers are reduced to observers at rest relative to one
another.
Now, here comes my point of confusion: If I were moving relative to the hubble flow, then I would not see an isotropic CMB and I would not see uniform expansion of the universe. If I formulated a model of the universe from such a frame, wouldn't I infer the need to include a preferred direction to the expansion of the universe (as evidenced by the anisotropic CMB and/or galaxy redshifts)? In other words, couldn't I interpret anisotropy as a fundamental part of the universe instead of as due to my motion relative to some preferred frame? If so, then how can we say that the universe is actually isotropic. If not, then don't we have a way to determine who is actually in motion, since only one particular frame will lead you to the correct conclusion of isotropy?
Submitted by beyer1981"AT"hotmail.com 1/12
I think you have this pretty close to correct!
One part that's a little wrong though is that it's not just motion relative to the Hubble flow that's subject to the Lorentz transformation. All motion is relative. So two observers, each in the Hubble flow, but moving relative to each other, would observe redshifts of each other's spectra. Comoving observers aren't the same as observers at rest raltive to one another. Although their motion (and observed redshift) relative to each other is particularly easy to calculate, because they have no "peculiar motion".
However, if you're moving with the Hubble flow, then you see no CMB dipole. That's because (in some sense) the CMB photons are also in the Hubble flow. Or in other words, the "rest frame" defined by the CMB is the same as the rest frame for the matter. This also makes sense from the point of view of asking about special directions. If I'm in the Hubble flow, then there's no special direction (like there would be if you were moving with some peculiar velocity vector). So I can't see a CMB dipole, because there's no way to choose which direction it would have its maximum in.
We can tell that we're moving relative to the Hubble flow because we can see the CMB dipole. All velocities are distorted a bit by our local motion. But we can remove this by looking at the CMB. And in any case, if we're only considering very distant objects, then the peculiar velocity becomes negligible compared with the relative expansion speed.
If I understand you correctly, it seems like we can tell that we are in an
isotropically expanding universe from any reference frame (not just
fundamental observers), provided we look deep enough into space? It seems
that regardless of our peculiar motion relative to the CMB, we can find a
background distance (lets say R), such that the maximum anisotropy in the
observed blueshifts/redshifts of the background stars is less than some
number, say eta. Therefore, the statement that the universe is expanding
isotropically is strictly true for fundamental observers and asymptotically
true for observers with peculiar motion?
Submitted by hwvolberg@yahoo.com 1/11
I think this is a bit confused.
An anisotropically expanding Universe would manifest itself as a shear in the expansion, i.e. a quadrupole, not a dipole. A special direction with blueshift and redshift on opposite sides of the sky simply implies motion of the observer. Genuine anisotropic expansion requires a "higher order" effect, like you get by squashing a sphere - so, for example, less expansion in both directions along some axis, compared with all perpendicular directions. That's an effect which you can't transform away by shifting to a frame with a different velocity.
Could gravity be the result of
times friction on the universe? Or do I have it mass backwards and it is merely
the mass of an object which causes space-time
to curve. To illustrate my thought I will attach a jpg. file showing the 4th
dimension as a depth, at an angle to 3D, as an ever-
expanding series of rings and 3D as a curved film over the surface.
As matter and possibly anti-matter expand around the
increasing depth of time it should appear to expand at an accelerated rate
expanding and simultaneously contracting, the
beginning being the end. Matter anti-matter compresses at the end the resulting
annihilation causing the high energy state of the early
universe. As time expands it pushes out at an angle to 3D matter which causes a
depression, Gravity then is a force of
pushing (Time friction) - rather then one of pulling. Denser more massive
objects cause - deeper depressions in space-time.
Time from this perspective is seen as a whole not linear as perceived by us.
Could this scenario be correct? The universe does not look like this it just
behaves like it.
Would our universe appear flat?
Would anti-matter then cause a lump where matter causes a depression?
Submitted by frostcarpentry"AT"gmail.com 4/12
Doug - This is an imaginative concept. But it has no mathematical rigour. We already have a theory to describe how mass curves space-time - it's called General Relativity, and it makes predictions which are good to many many decimal places. Of course what "causes" gravity is a much deeper question, and the issue of what made the Universe in the first place, and why it's expanding, are also questions to which we don't have the ultimate answers. However, it's pretty clear that GR describes the Universe on large scales very well. And we also know that that there's very little anti-matter in the Universe today (which is somewhat of an intriguing puzzle of course).
It's fine to keep speculating - but it has to be within the context of what we already know.
My Question is about the Friedman equation
Allow me to put forward my interpretation the of Friedman equation = Ho^2 =
( a dot / a ) ^2 = ( c / a ) ^2 = 8 pi G rho / 3 ...( k = 0 ) (lambda = 0 )
...
Solving for Ho = a dot / a = c / a = sqrt 8* pi *G rho critical /3
H = 68.67897 Km per sec per Mpc = 2.225736445 e-18 of a sec per sec per Mpc
C = 29979245800 cm
a = 1.346936016 e+28 cm
Solving for critical density = 3* Ho ^ 2 /8 pi G = 3 * ( 2.225736445 ) ^2 /
8 * pi * 6.67239 e -8 = 8.862054763 e-30 cm ^3/gram sec ^2
Solving for a = 29979245800 /2.225736445 e-18 = 1.346936016 e+28 cm = Hubble
length = radius of the visible universe
professor Scott there is a hidden coincidence in the Freidman equation which
I wood appreciate your comments to the following
(a dot /a ) ^ 2 = C * C / a ^ 2 = 8 pi G rho crit / 3
solving for G/C = 3 *C / 8 *pi *rho crit * a ^ 2 = 2.225736445 e-18 cm per
sec per Mpc = 68.67897 Km per sec per Mpc
sorry professor I had to go throw the above so I can put my question so here
it is ?
using the value stated above of Ho and rho crit of this epoch. How will the
value H rho cri and G very if the Hubble length is reduced by 1/2 =
6.734680080 e+27 cm
and kipping the coincidence of G/C = 3 * C / 8*pi*rho crit*a ^ 2 = H
Submitted by nick1st"AT"tpg.com.au 5/11
Sorry, I don't follow this.
The quantity "a" is usually thought of as a dimensionless number, set to equal 1 today (for example) and smaller in the past according to the Friedmann equation. You appear to have set it to some length scale by multiplying by the speed of light.
I'm not sure that what you have done is consistent, or that you have discovered anything new about this equation. In any case it is essentially just "kinetic energy = potential energy", and so not really a "new" equation.
I have questions about the accelerating expansion of the universe, mass, and
the speed of light.
Where is the energy coming from to continually accelerate expansion when
everything becomes more massive the faster it goes? Could this acceleration
reach the speed of light and if so, when? Could it go faster? Is light still
the limit if there is no apparent energy needed to increase speed regardless
of mass?
Has the rate of increase in mass been calculated, and is there a limit to
the potential mass reached? If mass or speed becomes infinite, what then?
Would the universe be full of particles or whole galaxies traveling at
infinite speed with infinite mass? What if there was a collision?
Submitted by benndoublenn@hotmail.com 12/12
These are good questions, which are mostly answered on other posts on this page! So I'll only be brief here.
The expansion of the Universe conserves energy locally - it has to do this, because the solutions we talk about are all derived from General Relativity, which has energy conservation built into it. The way this conservation makes sense is that pressure does "work" to make the expansion happen, and this exactly balances the energy density lost as everything gets more dilute.
If the question is about whether the total energy is conserved, or about why the Universe should be accelerating in its expansion, or even why it started expanding in the first place, then these are much harder to answer!
As to the relevance of the speed of light - certainly things can move apart at speeds faster than this. If you go far enough away right now, there will be galaxies moving away from us faster than the speed of light. This does not in fact contradict relativity (since, as I said, it's all consistent with General Relativity), because you can't observe anything to move faster than the speed of light.
And about mass: although sometimes it's said that mass increases with speed, I think that's a very cofusing and unhelpful way of thinking about the effects of special relativity. Really the mass stays the same (since it's just "rest mass") , while the momentum and the energy behave differently than they do at low speeds. So there's no increase in mass in the expanding Universe. Right now we're moving at faster than the speed of light relative to some very distant galaxies, but this has no effect on us!
How do we know that the Universe has no border? Is this more
of a philosophical statement, in the sense it "has to be borderless since it
is everything", or do we have any actual evidence for it?
Submitted by tuomas.kangasniemi"AT"hotmail.com 3/13
You're right, that there simply can't be an edge to the Universe, since otherwise what's beyond the edge would also be the Universe!
But the question is more physical in terms of searching for solutions for the whole Universe that are consistent with general relativity. Even a "positively curved" universe, with finite volume, still doesn't have an edge, for example.
As far as I have understood, the reasoning behind the flatness
or curvature of the Universe is based on empirical observation. However, the
Wikipedia article on the shape of the Universe left me quite empty-handed on
the question whether astronomers suggest we can infer the question of
inifinity vs. closedness on the basis of observation, or is this piece of
information just assumed. How is it?
Submitted by tuomas.kangasniemi"AT"hotmail.com 3/13
We assume that the Universe is the same everywhere (on sufficiently large scales), since that seems like it fits what we observe. Then we're looking for models with the same amount of curvature everywhere. Assuming this to be the case, then your question reduces to determining whether the overall geometry of the Universe is "flat", or "closed" (like the surface of a sphere in 4-dimensions) or "open" (like a negatively curved surface).
So far the Universe looks pretty close to flat. If it continues to look flat to more and more precision, then we will never know whether it is slightly closed or slightly open!
Only if we discover one day that the Universe is slightly closed, will be know the answer to this question.
I have watched a lot of
videos in which they say that, if anti matter hits matter, the whole
universe would explode, and they say they have never hit each other, would
you please answer this question and what exactly makes anti matter different
from matter?
Submitted by ryuhayabusa35"AT"gmail.com 3/13
You've been watching the wrong videos! Of course that doesn't happen, since there's plenty of anti-matter being created in cosmic rays etc. An anti-matter particle hitting a matter particle (of the same type) will result in annihilation of the 2 particles, and no more.
What is a scalar field?
Submitted by ryuhayabusa35"AT"gmail.com 3/13
Try this wikipedia page. The first part is quite understandable, and better than I would have written.
I just read "The Grand Design" by
Hawking/Mlodinow. It is over my head, but I was intrigued by a comment
that the expansion of space occurs outside of galaxy clusters but not
within them (somehow due to gravity??). It seems that this would lead to
different measuring sticks at different points in the universe. If the
speed of light is supposed to be constant then which measuring stick is it
constant relative to? How can a redshift be due to the expansion of the
universe if the yardstick also expands?
Submitted by waltertaylor"AT"shaw.ca 4/13
There are 2 ways to think about this. (1) You're only expanding if your local gravity is negligible compared with the effects of the Universe as a whole - and hence people, planets, solar systems, galaxies, and whole clusters of galaxies are stable self-gravitating entities, which are not expanding. It's just the space between them which is expanding - so they're getting further apart, even although their own sizes stay the same. (2) Everything was once expanding from everything else, but slightly more dense regions were expanding more slowly, and then as their own attractive gravity continued to do its work they slowed down and eventually started to collapse, then complicated physics took over, stars formed, things rotated, shared out energy and became stable self-gravitating entities (galaxies, etc.). Hence our region of the Universe was expanding once, but stopped a long time ago, and hasn't cared about the expanding Universe since then.
Could you please tell me the differnce between New and Chaotic
inflation.
Submitted by ryuhayabusa35"AT"gmail.com 5/13
Inflation is really just a very general idea. There are lots of specific implementations of this idea, which have been given different names. I suggest that a good place to start is the wikipedia article, which is here.
It sure looks like inflation has some of the right features to explain
where structure came from. But we don't know what flavour of inflation is
the best right now. Hopefully we can learn more by studying the CMB in
more detail.
H2>
I've been reading your website with
cosmological answers about black holes and so on. An interesting question
accrued to me regarding Schwarzschild radius Rs.
Rs = 2Gm/c2
According to general relativity, any body of mass m with radius less than Rs
is a black hole. This is the basic claim on which derivation of Planck
length and radius are based. If so, why there is Planck time even mentioned
in various universe timelines? As we know, it wasn't possible for black
holes to form in the early universe. If the formation of a black hole had
been possible, the Universe would have become a big black hole after the big
bang. But we know, this is not the case. This topic is also discussed on
your website.
Isn't then Schwarzschild radius meaningless, when explaining the young
Universe. When deriving the formula for Planck time, the possibility of
forming a black hole is essential. Logic conclusion would be, that Planck
time isn't important in the early universe cosmology. Please help me with
this issue.
Submitted by karlic.igor"AT"gmail.com 10/13
The issue here is simply that there's a time, earlier than which we don't know how to calculate physics, because we'd have to be able to do quantum mechanics in strongly curved space-time. One way to find this time is to equate the Schwarzschild radius (i.e. the gravitational "size" of the Universe) and the Compton wavelength (i.e. the wavelength of the Universe). However, this is just a convenient way to picture things. The core of the physics is simply that you can define a length scale (and a time scale) through fundamental constants which have to do with gravity and quantum mechanics.
No one considers that the early Universe was actually a black hole, since it doesn't have the "Schwarzschild geometry" (which is a point source embedded in a flat, no-expanding background), but it instead like the Friedmann-Lemaitre solution (uniform density in an expanding space).
Statement: There is no visible universe with out Me for Me.
Question is the Universe relativistic with out the Observer.
Is the Observer by his observation creates
the visible universe and changes the position of a galaxy of the Now
Universe.
Submitted by nick.stama"AT"gmail.com 12/13
This is a good question. It is related to some similar questions which have led to good debates among physicists for generations. For example, if there was just one electron in the Universe, and it was accelerating, then would it radiate? These kinds of hypothetical questions can be helpful for revealing underlying truths about the physics, even although they are far from practical.
I made a search thru your website and i found many questions similar to mine
and your answer is that the Big Bang was not from a single point but from
everywhere at the same time in an universe already very big. I find that
explanation hard to understand because it contradict Hubble Law saying that
as we go thru the past, the distance between any two points of the Universe
was getting shorter and shorter. So, at Time 0, the Universe must be reduced
to a single point and because of that the Universe was then infinitly hot
and dense.
Submitted by trai_nc"AT"hotmail.com 12/13
The point is that everywhere was closer together in the past, and so you can imagine running the clock backwards in time, with everything rushing towards you, but anyone else can also consider the same thing happening. So "everywhere" was the Big Bang. In other words you should picture the Big Bang happening everywhere, rather than in some localized region.
Can we point out towards the actual location of the big bang based upon the
direction of CMBs?
Submitted by "Muhammad Idris"
Yes! The big bang is located everywhere around us. So we can point out in any direction and we are pointing to the Big Bang!
What I want to say is:
[QUOTE]The inflation hypothesis explains the uniform distribution of
matter and energy by presenting the same argument used for the flatness
inconsistency - a small area of the nascent universe was "stretched" apart
resulting in an even distribution of matter and energy throughout the
cosmic plane. [Please note: This uniformity of distribution is applicable
for astronomically significant distances of galaxy scale.][END-QUOTE]
I want to mention the appropriate resolution for the observed isotropy.
Submitted by webmaster"AT"chapmanhilton.com 05/14
The usual idea is that inflation blew up all scales in the Universe by some huge factor. So that our patch of the Universe becomes very uniform. However, a crucial part of the picture is that at the same time the quantum fluctuations in the fields which made the Universe inflate, were also stretched to become very large, and these were the "seeds" for perturbations in density which grew into all the structure that we see in the Universe today.
So inflation smooths things out but also generates very low contrast lumpiness.
That The universe is accelerating according to current scientific theory
,witch means the expansion rate (H) per unit space is increasing .
What is confusing to me is the following the Hubble length HL=c/Ho if the
expansion rate is increasing,( HL) is decreasing. If the visible
universe,
is decreasing the critical density is increasing per unit space (
roh,crit = 3Ho^2/8piG) .Professor if you can give me an explanations
using the two
equations above it will be greatly appreciated.
Submitted by nick.stama"AT"gmail.com 01/15
The situation is a little different than what you describe here. It is a fairly common fallacy that in an accelerating universe, the Hubble parameter increases with time. In fact it is the scale factor that is accelerating, i.e. it's second derivative is positive. Since the Hubble parameter is (da/dt)×(1/a), then it turns out that today's Hubble parameter is slowly decreasing and will approach a constant in the far future.
You have been helping me to try to understand the Big Bang theory and its
postulations and Cosmology in general. I have a fair understanding about it
but now I have a problem with the flat universe postulation parroted by the
leading cosmologists. Surely the universe is not flat. sure its
curvatureless, Thats definitely true. Flat, No! All planets galaxies,
clusters etc are inside the universe right? That already throws away the
flat universe hypothesis. All diagrams trying to show the flatness of the
universe put the galaxies stars etc at the same level on top of the flat
plane purported to represent the universe. That is not the case with how
hosts of the universe are arranged in reality. They are at different levels
within the universe. My argument is that there are planets, galaxies all
around the earth and these that are all around the earth also have galaxies
all around them and so on. This gives a prismatic (prism shaped universe to
me) so why this flat universe crazy supported by all the cosmologists and
astronomers including Nasa.
Submitted by pd.delwaar"AT"gmail.com 02/15
In this context "flat" means not "curved", i.e. Euclidean space, as opposed to some non-Euclidean (or Riemammian) space. Within General Relativity it would be possible for the Universe to have a non-trivial overall curvature, but it turns out that the data indicate that space is just like Euclid described - except that it's expanding of course.
This isn't merely "parroting" by modern cosmologists, but is based on hard evidence. This can be reduced to a basic "triangle test", i.e. doing a large "quantity-surveying" type experiment and discovering that the angles of a triangle add up to 180°, as expected in flat space.
My point is, if available techniques to measure the shape of the universe
from within the universe point to a curvatureless universe this has several
inconclusive implications on the shape of the shape of the universe. It
does not mean that the universe is flat or Euclidean. A curvatureless
observable universe may still mean that the universe is still spherical but
it is so large, its curvature or spherical bend is so gentle, the
observable universe is simply too small in expanse to reveal any curvature.
A curvatureless observable universe may also mean that the universe is
still spherical but we are unable to identify the spherical curvature in
the observable universe from within the universe because the method we are
employing to establish the universe's curvature is flawed. A Universe which
is also endless/infinite in size/extent would not show a curvature just as
a prismatic universe (Prism shaped universe) would also not show a
curvature.
Submitted by pd.delwaar"AT"gmail.com 02/15
Ah, now we're in very good agreement!
In fact we only know from observations that the Universe is close to flat. But exactly flat is a kind of "knife-edge", which the Universe would evolve away from. Hence it's surely the case that on the largest scales we can probe, space is either slightly positively curved or slightly negatively curved. There are some theoretical reasons to prefer the positive case, and so that would be my best guess: the Universe has close to flat geometry, but is slightly positively curved. Although to be fair, there are also some theoretical reasons for preferring the negatively curved case instead!
For now this should be considered an empirical question. With the new Planck satellite data we know that the Universe is flat to within about 0.5 per cent. And hence for most purposes (i.e. calculating distances, etc.) we can assume that it's exactly flat and we'll be very accurate.
In the initial conditions of the
Universe, were there any space, or it created later?
Also, in physics how we can have HOT, very high density (condense)
state?
Submitted by ah.baghaeiarya"AT"yahoo.com 02/15
For the first question, I don't know what you mean by "initial conditions". If you mean the very very earliest times, then I have no idea what existed, or whether the concept of "space" is even useful. But for many cosmologists today, the earliest times to consider are the period of "inflation", which started off what we normally think of as a the "hot Big Bang model". And in the inflationary picture there is certainly the concept of "space".
For the second question, I'm also afraid I really don't know what you mean. There's nothing in principle that relates the density and temperature of a physical system. So you can have things that are hot and dense, just as you can have things that are cold and dense, or hot and "undense" (or cold and undense). The cosmological expansion naturally means that the early Universe was both denser and hotter.
It is well known that the ejecta from supernovae reaches very high
velocities and produces substantial blueshift in the center of the
observed object. These blueshifts have been observed and reported in
numerous papers.
The premise of the accelerating universe is based on the luminance of
distant supernovae being 10 to 15 percent dimmer than would be expected
from the redshift. Another way of stating this is that the redshift is
lower than would be expected for the observed luminance. Lower redshift
would result from the velocity of the ejecta. Yet the landmark original
papers which announced the acceleration of the universe made no mention of
correcting for the ejecta velocity.
What do you think about this?
Submitted by alanadler24"AT"att.net 03/15
Ejection is in both directions, so gives you redshift as well as blueshift. And you presumably have to use models of supernova explosions to fit this properly. I'm not an expert, but this isn't relevant for the accelerating universe result.
Through my interest to know
the universebetter, and with your help to do that, Iwill appreciate if
you assistance me to know the following questions. What
is the latest theory about the origin and fate of the universe?
2-Are Erwin Schrodinger equations, Heisenberg's uncertainty
principle,and Normal distribution applicable in modern physics?
3-What will happen if there is no gravity throughout
theuniverse? 4-Without gravity could a particle move at the
speed oflight?5-Also, kindlyassume that we have a box with
space and some amount of materials and there is alsogravity. What will
happen if suddenly, gravity switched off? Have wea normal distribution of
materials throughout the box?6-Would you please refer me to
the books or articlesabout space, gravity origin, theories of relativity,
big bang theory and other useful subjectsin this regard?
Submitted by ah.baghaeiarya"AT"yahoo.com 06/15
That's a lot of questions for one email! Let me try to answer them briefly:
(1) Inflation joining to the hot big bang model, evolving to endless coldness in a vacuum-dominated background; (2) Yes; (3) That's too hypothetical for me to answer (and some physicists would argue that you can't have space and time without gravity; (4) particles with rest mass can't quite reach c; (5) on a local scale nothing very exciting would happen if you switched off gravity; (6) there are lots of things on the internet, starting of course with wikipedia, which for these topics is typically written by physicists.
Is it possible to use universe expansion for energy generation?
Suppose we have a long massless rope. We tie one end to an object that is far
enough from Earth to experience universe expansion.
Then, we tie the end on the Earth to a power generator.
Due to universe expansion, the rope will stretch and we can get energy.
Of course, we will lose rope as time goes, but we can just attach more rope on our end.
Submitted by anaonymous 11/17
Thanks - this isn't one I've heard before (or at least it's a different variant).
Of course this is a hypothetical question, so obviously you couldn't ever do this in practice. But I don't think you can do what you suggest even in principle. One way to understand this is to realise that only objects in "the Hubble flow" are experiencing the universal expansion. Anything that has been affected by local gravity (e.g. a galaxy that started off a bit overdense and later collapsed to form an object) has stopped expanding at some point, and is now some self-gravitating part of the Universe, which doesn't care that the rest of the Universe is expanding. Thinking about this from the opposite point of view - anything that's an "object" (like a rope, for example) can't be expanding itself.
I read an article today on physics.org about the flaws in superconductor theory. It
stated "great increases in field can be seen I'm leaps rather than a slow steady
climb". This got me thinking. What if there is no dark matter at all and the affects
we see between galaxies is actually the affect of super cooled hydrogen in deep
space, which from what I understand is pretty abundant? What if the universe has a
mechanism ,within the physical properties of the matter that we actually experience,
that keeps things together and working as they should? What if the universe is just
a big superconductor and galaxies are all experiencing gravitational locking?I am
just spit balling a bit but it woukd be nice if we could prove once and for all that
either there is dark matter or isn't so we can get on with the progress and
experimentation with real life products that is to follow the discovery or
refutation.
Submitted by francis.mccann"AT"shaw.ca 4/18
There have been many attempts to connect ideas from condensed matter physics to situations in astrophysics, e.g. to perhaps explain phenomena that are related to dark matter or dark energy. However, I'm not aware of any such ideas that have proved to be useful. The basic reason is that the average density of the Universe is fantastically small - and hence the material isn't very "condensed"!
I would add two other comments. First of all, there is no dispute about the reality of dark matter. If you have read anything along these lines, then it's just the usual business of the internet being more chock-full of fringe science than real science. The evidence is plentiful and overwhelming. We can directly see the gravitational effects of matter that has to be "cold" and "collisionless", i.e. quite unlike the properties of regular matter. The second thing I'd add is that there are no realistic prospects of using this dark matter for anything! Although there are particles of dark matter streaming through us all the time, they are almost completely collisionless, i.e. they don't have a measurable effect on even the most sensitive pieces of measuring aparatus on Earth. So there's no way to harness them to do anything useful!
Given that the universe's expansion redshifts photons we receive from
components of the early universe, and that photon wavelength is inversely
proportional to photon energy, how exactly is the universe's total energy
conserved during expansion?
Submitted by rwortis"AT"trentu.ca 08/20
This is a very good question, which is often asked by people who are starting to understand the standard cosmological model. It has already been answered in various forms on this page. So if you don't like this answer, then please check out the other ones!
There's a basic fact about energy that's learned in introductory descriptions of thermodynamics, which states that for pressure to make a volume change work" is done. This is often called "PdV work" (i.e. pressure times a change in volume is part of the energy budget of a system). Taking any small piece of the Universe, the energy lost by the photons is exactly balanced by the "PdV work". This isn't surprising, since the standard cosmological picture is based on general relativity (GR), and GR is manifestly energy conserving.
What if LeMaitre erred when projecting backwards to a single event? What if
he had projected back to many, many events independent in space and time?
My question is regarding the degree of challenges (reinterpretations required)
vs. the benefits (tensions resolved, paradoxes and open questions resolved) if
scientists were to consider AGN SMBH and jets as the physical implementation of
the bang, inflation, expansion, and eventually crunch and bounce again in a
galaxy local cyclic process?
This requires suspension of disbelief of course, but we know that the
singularity does not make sense, and SMBH were rather rapidly thrust into LCDM
upon their discovery. For now let's suspend disbelief and imagine that an SMBH
can vent its extremely energetic core as polar jets under certain situations
(these jets sweeping up accretion disc material as well). Galaxy center SMBH
would do this intermittently and independently.
So here are my thoughts: [abridged] Submitted by 09/20
There are several things I'd like to say in response.
Firstly, I certainly don't picture the earliest moment of the Universe being a singularity. Rather I imagine there's some kind of quantum nature, which is difficult to picture and not yet fixed by observational constraints (plus perhaps not being properly understood until we have a full theory of quantum gravity). I think that most cosmologists think that the earliest moments were some kind of "quantum foam" (or whatever words you choose to describe it!), rather than a classical singularity.
Secondly, the standard cosmological model isn't just an idea that someone had one day and then everyone signed up as believers. It's a model that is based firmly on well-understood physics, with detailed equations governing its structure and evolution, enabling precise calculations to be made, which are compared with a huge body of observational data to test and refine the model. In order to propose a viable alternative, it's necessary to understand the conventional model in its full physics rigour, and then present the alternative in the same way, so that precise predictions can be made and compared with data.
Thirdly, the general idea you have here seems quite similar to ideas that have been suggested before. For xample, I would point you to articles on the Quasi-Steady State Cosmology", which were written around 1990s as a claimed alternative to the standard Big Bang picture (e.g. this historical review). However, this model is little more than a set of vague statements about how explosions associated with active galactic nuclei might somehow make a model that's a bit like the old "steady state" cosmomolgy viable. It is extremely hard to distill enough detail from these statements to enable precise calculations to be made - but when this has been done the model fails dramatically to fit the empirical information about our Universe.
[abridged]
I looked at various Large Numbers Hypotheses put forward over the last
100 years. And came to this relation ...
This equates the Hubble radius to fundamental constants.
H' is 1 / Hubble constant (I am subjectively using (4.383*10^17 seconds))
α' is 1 / fine structure constant.
G' is G/c^2.
k is Coulomb's constant.
e is the electron charge.
Do you think the equation is a numerological coincidence with or without
meaning?
Submitted by Sahil Gupta sahil"AT"spase.io 7/21
I'm afraid I think it has no significance. You appear to have found that the Hubble radius times the Schwarschild radius of the proton is approximately of the same order of magnitude as the fine-structure constant times the square of the Compton wavelength of the electron. The condidence is far from being exact, and it would be easy to make other combinations of various scales and constants that would be a closer match.
Does galaxy XMM-2599, a galaxy with stars burned out, stand as an observational
contradiction to the standard model? Why isn't there more discussion about
XMM-2599?
Submitted by Sahil Gupta sahil"AT"spase.io 3/22
I'm not aware of this particular galaxy being dramatically unusual. There are lots of galaxies out there and they all have different histories, depending on how they formed and how they interacted with their environments.
Given the variations in detailed properties, in general it's unlikely that a single object would be so extraordinary that it could rule out any model. Real progress in understanding cosmological structure formation is made through fitting the statistical information from large samples of galaxies, and not from looking at one object on its own.
Could micro organisms that our instruments can't pick out be part of the
supposed dark matter we conjecture in the Universe?
In either case, I would like an explanation if possible.
Submitted by Elie Bouroufail ebouroufail"AT"gmail.com 11/22
No, that's not possible. Although perhaps it depends how much you want to get into "science fiction" ideas!
We know that the dark matter isn't made of normal atoms, but is some other kind of stuff entirely. The technical jargon is that it has to be "non-baryonic". Since it's not made of atoms, then it presumably can't be something like space microbes.
I was watching a slow motion of a drop hitting the water.
It's my understanding that in our universe, at the very beginning, there was a
period of expansion. The the expansion subsided, but has started again. It's my
understanding that the universe is currently expanding faster than the speed
of light. In watching the video, I can't help notice the repeating motion as
the drop first hits the water, the ripples occur, but then the drop repeats
it's motion and effect but with less mass. I can't help thinking that due to
matter actually behaving like a wave that this might help explain the 2nd, 3rd
etc expansion of the universe. Is there an outside force such as the drop
creating these repeating cycles. Fractals?
Submitted by axel"AT"microzip.com 4/23
Those high-speed-camera movies of water drops are certainly fascinating to watch. What they're telling you about is that the physics of fluids is much more complicated than you might have expected. They don't have a strong analogy with what the Universe is doing.
As far as we can tell, the Universe started off in very rapid and accelerating expansion, a period called "inflation". During that period (at a time of something like a trillionth of a trillionth of a trillionth of a second) parts of the Universe expanded away from other parts at greater than the speed of light. This has consequences that match some observed properties of the Universe today (which is why we believe that this inflationary period might have actually happened).
A bit later in the history of everything, the expansion continued, but was no longer accelerating (i.e.g, inflation ended). I think that's what you're referring to in your question. But it's not the case that the Universe stopped expanding and started again. It has always been expanding, just at different rates.
I should add that although the water droplet videos have no direct connection with cosmology, there is an indirect relationship. The oscillating behaviour is like the acoustic modes (in other words, sound waves) that propagate through the Universe and leave their imprint on the cosmic microwave background. By studying the statistical properties (the CMB anisotropies) of these modes we can fit a precie model for what the Universe is made of and how it has evolved. It's all about waves!
We are grade five students researching dark matter. We have 3 questions for you.
What is dark matter?
Why did physicists think dark matter existed?
How is dark matter different from ordinary matter?
Thank you for your time.
Submitted by Molly.Robertson"AT"education.vic.gov.au 4/23
Those are good questions!
1. Dark matter is, as the name suggests, matter that's dark! More specifically it's a kind of substance that has mass, but doesn't give off any light.
2. We can tell there's dark matter there because of the effects of its mass through the force of gravity. This makes things move, and also bends the path of light rays. There's lots of evidence for the presence of dark matter, even although we can't "see" it in the same way that you can see a table or a planet.
3. We're made of ordinary matter, composed of atoms, which are themselves made of sub-atmoic particles (protons, neutrons and electrons). Ordinary matter can emit, reflect and absorb light. But dark matter does none of those things. Ordinary matter also interacts with itself, for example a ball will bounce off the ground - but two lumps of dark matter would basically pass through each other.
I hope this helps. Of course we don't fully understand what dark matter is, or why it exists!
I'm reaching out because I'm looking into this claim [on facebook] that the
un and moon are the same size. I would greatly appreciate a comment on
whether or not this is accurate.
Submitted by Anna Mock"AT"dailycaller.com 1/24
The Sun and the Moon are not the same physical size. The radius of the Sun is about 400 times the radius of the Moon. We know this from countless observations of the behaviour and motions of objects in the Solar System, as well as from spacecraft that have landed on the Moon or come close to the Sun.
The Sun and the Moon appear to be approximately the same angular size in our sky because the Sun is about 400 times further away than the Moon. So there is a sense in which they are "the same size" when viewed from the Earth, and that is indeed why eclipses occur (when the Moon closely covers the Sun from the perspective of Earth observers). This is the same sense in which a hand held out in front of you, so that it covers the Moon, could be said to be "the same size" as the Moon. However, most people would interpret "size" to mean the object's actual physical length that you would measure with a ruler - and this size is definitely quite different for the Sun and the Moon.
Why is the sky blue and why does the Sun appear red at sunrise and sunset?
Does the interstellar dust have anything to do with this?Submitted by yeunsung.park"AT"utoronto.ca
The atoms in the atmosphere preferentially scatter blue light more than red light. So the blue light that you see filling the sky has been scattered out of the sunlight and bounced around by all the atoms in the atmosphere. The sun appears red at sunset because the light is passing through more of the atmosphere when you see it low down rather than straight up. So enough of the blue light gets scattered that the remaining sunlight appears to be red.
This has nothing at all to do with interstellar dust, or anything else in the solar system. It's entirely due to the earth's atmosphere. However the light of many distant stars is "redenned" by passage through clouds of interstellar dust.
I have a pretty simple question that needs answering if you have the time.
OK, is it some sort of nuclear reaction that uses the microwave wavelengths
to excite molecules in foods?
I am familiar with the fact that nuclear reactions are caused by either fission
or fusion, but how does all of this work together (if it does at all)?
Thanks for your time and consideration.
Submitted by Autumn_Moon"AT"msn.com
There are lots of different sorts of "transitions" (moves between energy levels) in matter. Each transition will have a characteristic energy range. The basic point is that microwave have nowhere near the sorts of energies required for nuclear reactions, and so you needn't worry!
Transitions happening in the nuclei of atoms are very high energy things, and so they involve gamma-rays, or at least x-rays, ie photons of the highest energies. So when fusion or fission happens, there's a lot of energy involved, and the relevant photons are very high energy (very short wavelength).
If you wanted to zap the nucleus of an atom you'd need high energy gamma rays. This is not something you could do accidentally in the home! It would require a particle accelerator or a strong radioactive source.
Transitions between the electrons in an atom are a much lower energy phenomenon. These involve photons which are typically in the visible part of the electromagnetic spectrum. Their wavelengths are at least 1000 times longer (and energy at least 1000 times lower) than the lowest energy x-ray that might be involved in a nuclear reaction.
But there are even lower energy transitions which can occur in matter. Molecules (atoms bonded together by overlapping clouds of electrons) can vibrate and rotate. A particular molecule will have a discrete set of energy levels associated with these motions. Transitions between these levels typically involve photons in the microwave regime. Their energies are about a factor of 1000 less than those responsible for electron-level transitions, and maybe a million times below those involved in transitions within a nucleus.
Your microwave oven is a generator of microwaves, which have wavelengths which are measured in millimetres. When you zap your food what's happening is that the microwaves are causing some of the molecules to shake around. Then that shaking is transferred to the rest of the food as heat and your food cooks!
I am interested in plotting the course of the sun as it shines
throughout the day. More specifically I would like to be able to predict
the exact position of the sun in the sky from anywhere on the globe
any time of the year ... (abridged).
Submitted by jlebel"AT"ibm.net
OK, not exactly a question on the CMB, but let me answer it in the most useful way I can think of, and that is to suggest books which are useful for a whole range of similar questions.
If you are interested in figuring out the exact position of the Sun, the Moon, the Earth's direction relative to the CMB, or whatever, there are a number of avenues to pursue. First of all there are several decent pieces of software you can buy, which are fairly accurate at showing the positions of celestial bodies in the sky at any location on the Earth at any time, etc. Secondly you can try to write your own computer programs to calculate things in which you might be particularly interested. And finally you can dig deeply into all the corrections for this that and the other thing (non-spherical Earth, non-circular orbits, precession, etc.) in the more serious literature.
A very good place to start is the excellent book by Peter Duffett-Smith, called "Practical Astronomy with your calculator", or one of his recent additions: "Astronomy with your personal computer" or "Easy PC Astronomy" (all published by CUP). For more accurate formulae and tables the authoritative reference is the "Astronomical Almanac" (published annually by the US Naval Observatory and the UK Royal Greenwich Observatory). The final details of how to get things accurate to milli-arcseconds will be found in good books on celestial mechanics, spherical astronomy and geodesy. But be warned that getting the most accurate answers can be complicated, and you'd be advised to start with the simplest formulae!
My question is about cosmic radiation and how it might affect astronauts,
moon colonists, etc (abridged).
Submitted by Jay40swm"AT"aol.com 9/98
I've had several questions like this, which I think sometimes are confusing "cosmic microwave radiation" with "cosmic rays". Cosmic rays are high energy particles travelling through space, which are potentially hazardous to space travellers, so that astronauts have to have fairly thick suits and shielding on their vizors. Cosmic radiation is the general term for any old thing radiating from some cosmic source. Normally when we say "radiation" we mean photons rather than particles (although at the highest energies you can't really tell the difference). The dominant form of cosmic radiation is the CMB, although there are photons at other wavelengths kicking around in space too!
Cosmic Microwave Background photons have very low energy, and very low flux (compared with a terrestrial source of microwaves for example), and are completely harmless. That's a good thing, since most of them get through the Earth's atmosphere, and so they're streaming through you at the rate of zillions per second, irrespective of whether you are in space!
Is it possible, with progress in all areas (technology, biology, etc.)
that in billions of years, that intelligent life might survive forever in
an expanding universe, and change the ultimate fate of the Universe?
(heavily abridged)
Submitted by dbrodara"AT"sk.tel.hr 9/98
Your pondering about life and the fate of the Universe is certainly along similar lines to what many other people have thought about before you, and presumably many people will still be asking about long after we are gone! Let me say that some of this musing is perfectly sensible, but occasionally it goes off the rails (do I need to give examples?). Partly such questions are peripheral to Science, since there isn't obviously any detailed model from which you can make predictions and carry out tests. So often such questions are regarded as "metaphysical". However, I think it's important for scientists to acknowledge that it's obviously 's fun to speculate about such things. But it's also important to remember not to take such speculation very seriously!
Most physical scientists regard life as a very inconsequential part of the Universe. Exactly how far advanced we can become is the stuff of science fiction books (which we all enjoy!), but not necessarily something which is realistically achievable. It seems unlikely that life will continue "forever" in an expanding Universe. But in principle, if you can think of more and more elaborate ways of using available energy, then you could imagine life sustaining itself for a very long time. Whether life could ever change the fate of the Universe is way, way speculative - so your guess is as good as mine!
Still, the Universe isn't going to change too much for the next 100 billion years or so. So there's no need to get too worried about it now!
If light traveling through vacuum takes time to do
so, why? To my mind something can not take time to travel though a
nothing? What medium is light traveling through to be as slow as it is?
(dark matter?)
fleggfam"AT"recorder.ca 9/98
I'm trying to understand what assumptions you are making to ask this question, since I'm afraid you have things a little backwards here. You can think of light as either waves or particles (like anything else, this being at the heart of quantum mechanics). From the particle point of view, then there's no problem in imagining that photons (particles of light) just travel unimpeded through space at whatever speed they choose. The problem might come when you try to picture light as a wave, and ask questions like "a wave in what?"
Such questioning led people (100 years ago) to suppose the existence of an "ether", or a hypothetical substance spread throughout space which is the thing that light is a wave in. Thinking along these lines leads to speculation that there is an absolute frame of reference in which the "ether" is at rest. But experiments showed that light travels at the same speed in the direction in which the Earth is travelling through space as it does in the perpendicular direction. So where was this ether?
This was all elegantly sorted out through a combination of Maxwell's electromagnetic theory and Einstein's special theory of relativity. Maxwell showed (around 1860) that electric and magnetic fields are part of the same phenomenon. One outcome of his electromagnetic theory is that there exist waves of oscillating electric and magnetic fields which move through space at a particular speed, and this speed turned out to be identically the speed of light. So these oscillating electric and magnetic fields are light. In other words light is a form of electromagnetic radiation, and it doesn't need a medium in which to travel. It was in trying to understand these ideas at a more fundamental level which led Einstein to his Special Theory of Relativity, central to which is the idea that the speed of light is independent of the motion of the observer. This effectively did away with any need for the ether, and also the idea that there is an absolute reference frame (although there are subtle issues here to do with the CMB, which I have discussed above!).
Light travels through the vacuum at a speed of 299,792,458 metres per second. In a material (e.g. glass) light is impeded, and actually travels slower by typically a few per cent. This is also fully explained in Maxwell's theory, since the electrical and magnetic fields behave differently inside some material than they do in empty space. So CMB photons move at the speed of light through the Universe, maybe a teeny bit slower through the interstellar medium of our Galaxy (and any others they pass through), and then a little bit slower again when they pass through the Earth's atmosphere.
Can radation from a sattelitte dish or television set be harmful to me?
Submitted by pisanochas"AT"webtv.net 11/98
I answered a similar question somewhere higher up in this document, about whether microwave radiation is harmful, and the confusion with ovens etc. So let me just add a few extra comments here.
One thing to get very straight is that the word "radiation" just means something that radiates from a source. The colloquial connotation is that "radiation" is something that makes you grow two heads and glow in the dark! But all types of light are electromagnetic radiation, and mostly pass through us with no effects whatsoever. The highest energy form of electromagnetic radiation, gamma-rays (and high-energy X-rays), can indeed be harmful. Extreme ultraviolet radiation isn't too good for your skin either. But most infra-red radiation, microwaves and radio waves tend not to interact with your body much at all. Very intense microwaves of the right frequency range can interact with molecular bonds, causing the molecules to vibrate and heat up - which is how a microwave oven works. But the levels of radiation involved with radio and satellite communication are very very small indeed compared with this. So no danger that we're all being cooked by microwave radiation from satellites!
Another way of looking at it is that if such microwave radiation could possibly harm us, then we'd have been cooked by the CMB radiation long ago!
Back in the mid-eighties, I was loaned a physics book of cartoon
illustrations. It leaned heavily towards particle physics and quantum
cosmology. I can't recall either author, title or publisher. I thought
maybe someone such as yourself may have come across this book.
Submitted by s.fine"AT"utoronto.ca 12/98
Hmm. I'm not sure. Not a very CMB related question, but since I use such cartoons regularly when I give talks, I suppose I'm as good a person to ask as anyone.
There are books of cartoons by Sidney Harris (who has published in Scientific American and similar places), which contain many physics-inspired examples. There's a related web-site called Science Cartoons Plus! One of Harris' books with a lot of cosmology cartoons is called "Einstein Simplified". There's also a book called "The Cartoon History of the Universe; From the Big Bang to Alexander the Great" by Larry Gonick, which includes some cosmology in the first section. There's more in "The Cartoon Guide to Physics" by the same author.
Does anyone else have other ideas?
I have a report due in two days! I'm a bit lost! ...
Submitted by DenCharlie"AT"aol.com 4/99
I have received several requests like this. Let me try to answer in this way. I'm not trying to be rude or insulting, but, are you really suggesting that I do your homework for you?!
There's lots of information on these web-pages, as well as several others that I have provided links to. Obviously the trick is to efficiently find the places which have the level of information that you require. Good luck!
How can you transmit a message via radio, I mean like radio
stations or via cellular phone? and how can you receive those transmissions?
Submitted by cesarbaq"AT"gye.satnet.net 4/99
Not exactly a CMB question, but since I've received several like this, I'll answer it anyway.
Radio waves are electromagnetic radiation (like light, x-rays, UV, etc) - and are the name we give to EM radiation with the longest wavelengths. Microwaves are basically just the shortest wavelength sorts of radio waves. You transmit the radio wave by wiggling electrons in an aerial, and receive them the same way, by sticking an aerial in the radio waves, which wiggle the electrons and set up currents in a circuit.
The actual messages are made by sending out a radio signal which changes in some way. Either the frequency of the signal is varied, called frequency modulation (FM) or the amplitude is modulated (AM). You have some electronics at one end which makes the signal vary in some way as you speak into a microphone, and then at the other end similar circuitry decodes these variations and turns them back into sound. There's obviously a lot more to it than that, of course, but that's the basic picture!
In a cell-phone, the signals you receive tend to be quite weak, and so you need a fairly sensitive detector, which will amplify the signal so that the rest of the electronics can decode the message and play it through the ear-piece. The sorts of transistor detectors used in cell-phones are in fact very similar to those used to detect the Cosmic Microwave Background radiation.
I'm a student of (analytic) philosophy
and I have chosen to write a paper
on the relationship between metaphysics and science,
and insofar as it relates, the relationship between
cosmology and ontology. I was hoping that you would be willing to
give me your opinion on the statement that in order to have a complete
cosmology one must also have a complete ontology.
Submitted by "E.M. Kronoff" < deliciolae"AT"yahoo.com 5/99
Gosh, I'm not sure I understand this question!
Physical scientists are notorious for avoiding any hint of metaphysics in their research work, and cosmologists are no exception. Even if it is common to think about the philosophical aspects of studying the Universe as a whole, and to discuss such things over coffee with colleagues, it is very uncommon for any of this discussion to appear in papers.
I'm sure that you are considerably better informed on these aspects than I am. So it's unclear that I can offer very much help. However, I can at least tell you the basic philosophical framework in which physical cosmology is carried out -- a framework which is implicit in the conventional scientific approach. And that is that the physical Universe exists as the basic external reality. Physical objects are "real", at least in the sense that they follow laws which can be derived and understood, and that they will follow the same laws tomorrow, and that in general the scientific method (experimentation and theoretical calculation) works in understanding the detailed nature of this reality.
Having said that, there are questions which one can think of, which at least live on the edge of this world-view, if not outside it entirely! Things like "is this the only Universe?", "is there anything outside our Universe, or that existed before t=0?", "why does the Universe have the properties that it does?", "could it have had different properties?", "can we ultimately understand everything through grasping the full laws of physics?", "could there be some aspects of the Universe which are essentially incomprehensible?", "do we play any meaningful role?", etc., are all the sorts of question which cannot be entirely addressed within the study of physical cosmology. There is debate about whether such questions are testable, or whether they will always be metaphysical. And many people bring up Anthropic ideas to answer some of them. Certainly I have my own answers to such questions, but probably this has little to do with my expertise as a cosmologist, and it's equally certain that I can find colleagues who would disagree with me on each point.
That's enough rambling, and time to put my scientist hat firmly back on my head! I hope this has been at least some help to you.
Do you know where I might find literature on the debate on these big questions?
Submitted by "E.M. Kronoff" < deliciolae"AT"yahoo.com 5/99
A good discussion of Anthropic ideas, and related topics, can be found in the recently- published book by Prof. Sir Martin Rees, called "Before The Beginning: Our Universe and Others". I highly recommend this book (although of course I am biased, since he was my graduate supervisor!).
I have a theory about cosmic radiation and how it might be effectiing the
aging process. In a science
project I saw a few years ago I thought I noticed that these rays could be
stopped by water vapour... [abridged]
Submitted by Donbhafsf"AT"aol.com 5/99
Let me try to sort out one or two things for you.
Firstly, you may have confused the Cosmic Microwave Background (low energy photons, originating in the early universe), which I study, with Cosmic Rays (high energy particles created in the outer envelopes of stars, or explosions of stars, or in other active phenomena in our Galaxy, or some as secondary rays when CRs hit the Earth's atmosphere), which I don't study. Even although I've answered similar questions before (see above), I'm not an expert.
There's nothing mysterious about Cosmic Rays, they're just very high energy sub-atomic particles raining down on us from space. They get absorbed by pretty much any kind of substance, with thicker and thicker layers being required to stop higher energy ones - and the very highest energy cosmic rays pass through most anything.
If there was no atmosphere on Earth, then we might be in trouble from all the Cosmic Rays. Astronauts wear protective suits partly to shield them from some of the Cosmic Rays. I believe that there is a connection between cosmic rays and some cancers, but they're certainly not the reason for all human disease, aging etc.
There's no magical property of water that makes them stop cosmic rays better than other substances. I suspect that what you recall seeing was some sort of "cloud chamber" or "bubble chamber". This is a detector for high energy particles which uses water vapour (or something similar), which gets nucleated into droplets by the passage of a Cosmic Ray. Many science museums have such things set up as displays to show that there are Cosmic Rays passing through the room as you watch!
I hope this is of some help. For some more professional help on Cosmic Rays you might try here.
I need to know the effects of cosmic radiation on human DNA.
Submitted by stolau03"AT"stmarys.kzn.school.za 8/99
This is another question which is similar to one I've answered before. But let me do so again, and also give a useful url.
The basic thing to point out is that "Cosmic Rays" are entirely different from the "Cosmic Microwave Background" (which passes through you by the billions every second with no effects whatsoever!).
A good source of information on the harmful effects of high energy radiation can be found at the U.S. Environmental Protection Agency page here.
What is the for the length of time it takes light to travel one
centimeter in a vacuum?
Submitted by shanana"AT"desoto.net 9/99
The speed of light in a vacuum is a fundamental physical constant. In fact it has been fixed at a precise value, so that once you have a definition for the metre, then you also have defined the second. The definition is that c = 299,792,458 km/s. So light travels about 3 × 1010 centimetres per second.
Light travels slightly slower through any real material. Typically it's maybe a few per cent slower in glass for example. Microwaves are just another form of light, and so they also travel at c in a vacuum. Since the CMB photons have travelled through almost completely empty space for most of their existence, they travel at the speed of light almost the whole way, and a tiny little bit slower through the last bit of their journey towards us through the Earth's atmosphere.
Is it possible that in just few decades ,with theoritical advances and
technology, we are going to acheive a full understanding of the
Universe. And what might be the consequences?
Submitted by kalin"AT"blazemail.com 9/99 I certainly hope not!
It does seem feasible, with the potential of the Planck satellite, together with several other ambitious astrophysical projects, that within about a decade we may have the basic answers to some of today's biggest cosmological mysteries. We will probably have a good idea of how fast the Universe is expanding, exactly how much dark matter it contains, and whether it is likely to expand forever, as well as some strong hints about the very early history of the Universe, and in particular where all the structure came from, and how it developed into galaxies.
However, that's far from being a "full understanding of the Universe"! I can certainly think of many questions which I don't expect to be answered on that timescale. And I'm sure that further progress on today's big mysteries will lead to other questions that we haven't even thought of yet!
If we ever really came to understand the whole thing, then the obvious consequences are boredom. It's hard to imagine coming to work every day and having no obvious research projects to do because we understood everything!
Why is the night sky dark?
Submitted by Punkrocker111"AT"aol.com 10/99
I'm sure you know the answer to that question! Noone asks that unless they've heard of "Olbers paradox" and its resolution.
In case anyone else reading this is confused, let me explain that Olbers Paradox is an idea dating back hundreds of years and discussed independently by many philosophers and scientists (including Olbers). The idea is that if the Universe was static, infinite and eternal and filled with stars, then the sky would be incredibly bright. You can show this either by adding up the contribution from a bunch of spherical shells around you, or by realising that in such a universe every line of sight hits a star eventually.
The resolution is that of course the Universe is neither static nor eternal (and may or may not be infinite). Galaxies evolve and the Universe is expanding. So the sum over all those concentric shells has a cut-off, since eventually you get to a distance when you are seeing the Universe before there were any stars or galaxies. On top of that the light is redshifted in an expanding Universe, reducing its brightness.
Of course there is some brightness of the night sky, casued by the combined effect of all the stars and galaxies out there. So even the "dark sky" isn't absolutely dark. The brightness of this background light depends on what wavelength you look at. And in the microwave range it's the brightest of any wavelength. That's the Cosmic Microwave Background!
I was wondering if you could tell me the wavelength, ...
of a microwave oven?
Submitted by PlevyGirl"AT"aol.com 12/99
I've had several similar questions, so it's about time I answered one.
Let me be clear. I am not an expert on microwave ovens! The only relationship between microwave cooking and the CMB, is that they both involve radiation of approximately the same wavelength. However, in a microwave oven the energy density of the microwaves is many many orders of magnitude larger than it is in the rest of the Universe.
For more information about microwave ovens see the Microtech's Microwave Oven FAQ" page
You may be interested to add a link to your CBR site to a recently
created web site that offers a critical look at the Big Bang and the
interpretation that the CBR arises as the result of the BB.
Submitted by skeptica"AT"pacbell.net 2/00
Doesn't sound too much like a question to me. But in any case, here's the link.
I'm always happy to hear about alternative viewpoints. I have several such links in the "hat-stand" section of my Cosmology page! I must admit to never having understood the urge to try to disprove the Big Bang model. From any reasonable grounds it seems like an attractively simple idea. Everything else I've heard of is both more complicated and fails to explain the observed Universe.
I have been asked to deliver an introductory lecture on the topic
"Extreme high-energy cosmic rays in view of the microwave background
radiation" to a supposedly general audience.
Could you recommend some literature which might help ? What are
high-energy cosmic rays? What is their connection to microwave background
radiations?
Submitted by Sam.Subbey"AT"petec.com 3/00
I have to say I'm puzzled by why you are giving a talk on such a specialized topic without understanding the topic! Is this some form of torture imposed upon potential job candidates somewhere?
In any case, cosmic rays have very little to do with the CMB. They are high energy particles arriving at the Earth's upper atmosphere from space. They have a range of energies and composition, but are generally light nuclei arriving from the Sun, other stars, supernovae and external galaxies. The highest energy cosmic rays, about which we have been learning a great deal in only the last few years, can have energies above 1020Joules in a single particle - which is the kind of energy in a decent fast-ball!
One mystery is where such extremely high energy cosmic rays can come from. The connection with the CMB is that there's a process by which such ultra-high energy particles would scatter off the CMB photons on their way to us (technically referred to as the GZK cut-off). Since there don't seem to be any preferred directions, the best guess would be that they come from distant active galaxies - but in that case they would have been scattered off the ubiquitious CMB photons before they got here. There's a debate about whether this might imply some bizarre source for these cosmic rays, or whether they might be exotic particles of some sort (or whether some more mundane explanation is more likely).
One site which explains this in more detail is the Pierre Auger Project web page.
If all light from modern universe, corrected for redshift, (corrected for
large enough area to be representative) were averaged, what would be the
effective or average temperature?
Submitted by jjk"AT"ngdc.noaa.gov 5/00
This is a very good question!
To answer it, let me re-phrase it slightly differently. The diffuse emission coming from the sky can be estimated at different wavelengths. In appropriate units an estimate of the background light is just proportional to the energy density. You can find my own version of a plot of such estimates as a postscript file here, with the vertical axis being proprtional to energy density. The CMB dominates over the backgrounds at other wavelengths, by a fairly substantial factor. The next most significant background is the far-infrared background, caused by the accummulated emission from dusty galaxies. Then just a little below that is the optical background, caused by the optical photons from all the galaxies along an average direction. The UV background isn't too well determined yet, but is certainly lower. The x-ray and gamma-ray backgrounds are fairly well determined and are lower still (believed to be due to the agglomeration of active galaxies).
The answer to your question
depends on which wavelength region you are most interested in.
If we take the optical background light, then it's a factor of around 1000
less energy density than the CMB. Since the energy density of a blackbody
is proportional to the 4th power of the temperature, then the blackbody
temperature corresponding to the optical light would be about
41000 ( 5)
times smaller than the CMB
temperature. Let me be clear that the optical background is not
a blackbody! But if you spread out all that energy and let it relax into a
thermal spectrum, then it would correspond to a temperature of around
0.5 Kelvin.
Suppose: ...
Instead of
expansion, we are now experiencing duration or rate-of-event-occurance faster
than we were in the past. ...
As we look back in the past ...
we see a constant red shift because things happened slower then.
Proof:
The speed of light as measured over the last 300 years has been steadily
decreasing. ... [abridged]
Submitted by DLZC"AT"aol.com 6/00
The premise of this question seems to be based on the idea that there is evidence for the speed of light having changed over recorded history. There is no such evidence. This is one of those myths that refuses to die, despite the evidence having been quite poor in the first place, and lots being written about how the claims don't stand up to detailed scrutiny.
Despite that, it is of course possible that over much longer periods of time the speed of light could have been different than it is today, without violating any direct experimental limits. The idea that the speed of light may have been different in the early Universe is one which has been looked at in some detail recently by theoretical physicists. However, one has to be very careful about what the speed of light may have been varying with respect to! In fact when you go through the details of physical thoeries, it turns out that there are only observational consequences if you vary dimensionless constants. So, for example, you can ask how things would be different if gravitons (which are involved with the gravitational force) had a different speed than photons. But the speed of light varying on its own makes no sense. In fact today there are various indirect means of determining that gravitons move at speeds within about 1 per cent of c, the speed of light. This could in principle have been different in the early Universe.
There is no way I know of in which a variable speed of light could be used to explain cosmological redshift. However, there are ways of making the Universe avoid an early period of "inflation" by having the speed of light be much faster then, so that it only appeared to have gotten exponentially bigger. This is at least something of the flavour that you are suggesting, and is an idea which is taken at least mildly seriously. However, although these ideas have been looked at, there is currently no good motivation for believing that the speed of light really may have been different in the past. And certainly not during the tiny amount of time that humans have been doing experiments to measure its value.
Is there any connection between Cosmic photons and life [abridged]
Submitted by d_sideris"AT"yahoo.com 8/00
This is a question, I think about Cosmic Rays, rather than the Cosmic Microwave Background. Particle from the CMB (microwave photons) are such low energy that they play no obvious role in our lives, or in the history of life in the Universe - other than the fact that the CMB affected the evolution of the whole Universe at very early times of course!
Cosmic Rays, on the other hand, are high energy particles from the Sun, other stars, supernova explosions etc., whizzing through our Galaxy and raining down on Earth. Really the only thing in common between Cosmic Rays and the CMB is the word "cosmic". For more information on Cosmic Rays you might want to try this Cosmic and Heliospheric Learning Center page. It is believed that cosmic rays are one of the factors that can lead to mutations, which may be important for the evolution of life. However, this is way, way out of my area of expertise. I suggest that you search the web - but beware that there's a lot of junk out there on related topics!
I am having a bit of trouble finding background information on
the subjects of Pressure, Vacuums and Density... (abridged)
Submitted by ARubinlat"AT"aol.com 10/00
Although this isn't specific to the CMB, I'll try to answer this since it allows me to point to some places where you can find basic information on some fundamental concepts in physics. A clear idea of what is meant by things like "energy", "density", "force", "temperature", "mass", etc., will help understand what is going on with this cosmic microwave background business, as well as with the rest of Physics!
One good place to start is with the Physics FAQ from usenet. I'm not sure that there's an ideal dictionary of Physics available free on the web. But you might like to try Eric Weisstein's Treasure Trove of Physics or the Academic Press Dictionary of Science and Technology, which are quite useful. At a simpler level, but more relevant to these pages is the Imagine the Universe! Dictionary.
For one of my projects ... I have chosen
to study the relationship between the brightness of a star you can see,
and the brightness/amount of background light. ... However I was
having a bit of trouble finding some information about this topic [abridged].
Submitted by iwasaki"AT"mail.cstudies.ubc.ca 11/00
This is a question about the sky background at optical wavelengths casued by the glow of the sky, rather than about the CMB. Hence I am far from being an expert. So let me just point you at some useful places.
A good technical paper is "The 1997 reference of diffuse night sky brightness" by C. Leinert et al., Astronomy & Astrophysics Supplements, volume 127, page 1. This contains a great deal of information on glow from the night sky, as well as diffuse emission from astronomical objects. It was prepared by members of the Commission on "Light of the night sky" appointed by the International Astronomical Union, and so it is the authoritative reference. However, it probably has more detail in it than you ever imagined!
There is a great detail of material available on the web on the related topic of what astronomers call "light pollution", i.e. the problem of stray artificial light interfering with astronomical observations. I suggest that you search for relevant links to find out more about this topic, and that this may in fact be what you are looking for.
I need to know the ratio of the number of photons generated when
the frequency is changed. I am aware that the "energy" per photon
doubles if the frequency doubles, but what about the "number" of
photons. [abridged]
Submitted by mpaulk"AT"abc32.com 11/00
Of course this depends on whether you are making new photons or not. Let's focus just on the CMB, where the spectrum stays very close to a blackbody as the Universe expands (except at very early times, when there are particle-antiparticle annihilations etc.). So if we consider the CMB and run the clock backwards, then as the Universe shrinks, the frequencies of all the photons get higher and the density gets higher too. The number of photons per unit volume is simply proportional to the third power of the CMB temperature, or alternatively the third power of the peak frequency. For an individual photon, the energy is proportional to the frequency (Planck's Law). The energy density is then proportional to the fourth power of the temperature.
For blackbodies things are pretty simple!
Do we know whether Mars ever had life at any time during its past? What
argues in favor of the position that it may once have harbored life?
Submitted by flirtalert007"AT"hotmail.com 12/00
This is way off topic! There are many web-pages devoted to it though, and I would suggest starting at the JPL Mars page. Let me not shrug this off entirely - it is a fascinating question. There is certainly evidence to support the idea that ancient Mars had liquid water, and indirect evidence for the possibility of life. You should appreciate that the study of this topic is effectively a combination of astronomy and archaelogy, both of which are observational (and hence indirect) rather than experimental (and hence more directly verifiable) sciences. So the evidence is hotly debated among experts in that field.
The CMB plays essentially no role in the question of the development of life, although the study cosmology does teach us that the Universe is a big place, and that there are lots of chances for life to have developed elsewhere. Hence proects like SETI@home.
What is the connection between the average lifetime of Galactic
civilizations and the possibility of our someday communicating with them?
Submitted by collegechick247"AT"hotmail.com 12/00
Another unrelated question! I wonder if you know the last questioner?
In any case, this is related to the famous "Drake's Equation", which is a meant as a guide for assessing how likely it is that we will communicate with extra-terrestrial civilizations. You can find out more about this topic on the web (e.g. at the SETI institute Drake Equation page), or in many introductory astronomy textbooks.
One thing that i'm puzzled with is how does math/physics play a role in
the explanation of the operation of the solar system.
Submitted by boolani"AT"sprint.ca 1/01
I'm tempted to say "mathematics plays the same role in the solar system as it does everywhere else in the Universe"! But let me try to be a little more helpful. Basically you can't really understand the workings of the physical universe without studying mathematics and physics. So if you are a high school student (for example) who is interested in learning more about how the Universe operates, then you need to work hard at those subjects! There are plenty of books and web-sites out there where you can learn, for example, the principles behind the dynamics which operate within the solar system. It's all physics and mathematics!
The relationship between how a radio wave is reflected off a hole smaller
than its wavelength and the way the radio wave is represented propogating
through the air as a SINE WAVE does NOT mix. ...
It seems that ... the AMPLITUDE would be what's
keeping the wave from entering the hole, because the amplitude may be too
fat. It's like taking a broomstick that would fit through a small hole and
saying it won't go through because it's too long(kinda like wavelength).
What gives? [abridged]
Submitted by trixae999"AT"hotmail.com 1/01
I think you've slightly misinterpreted the drawings of electromagnetic waves, which are meant to be an analogy.
But let me back up. All forms of light, radio, X-rays, etc., are different kinds of electromagnetic radiation. In other words they are travelling disturbances in electric and magentic fields. This includes the radiation making up the Cosmic Microwave Background. The amplitude of electromagnetic waves is the strength of the electric and magnetic fields involved. The analogy here is with water waves, or waves on a string, where the amplitude is the displacement (or height) of the wave in the direction perpendicular to the direction the wave is travelling. But this is just an analogy. And if books describing these waves sometimes draw them as things that look like waves on a string, it's just because it's hard to draw oscillating electric and magnetic fields and have it look very helpful!
So the amplitude of an electromagnetic wave has nothing to do with a length - it's not a displacement or a height, like the wiggles on a rope. This amplitude then has nothing to do with diffraction (and related phenomena) for such waves, all of which is determined by their wavelength. It's hard to get radio waves through a small hole, while X-rays will pass through quite small holes. One way to think about this (which I hope will be helpful, and not replace one limited analogy with another!) is that the little packets of electromagnetic energy are only properly described by quantum mechanics - this says that they behave more like waves when looked at on scales shorter than their wavelength, and more like particles when looked at on larger scales. So if the hole is much larger than the wavelength then the electromagnetic wave-packet just behaves like a particle and passes straight through. While if the hole is small enough then you have to consider the wave effects.
i need some data on experiments made with black holes and stuff
Submitted by DsSw33ti3sM"AT"aol.com 1/01
I'm not aware of any experiments done with black holes. It would be cool though if someone could make black holes in their lab and investigate their bizarre properties!
This would make it very much easier to prove the existence of black holes. At the moment the evidence is quite indirect, although very compelling. It comes from a combination of observations of stars with unseen binary companions and detailed observations of the nuclei of some galaxies.
The "tired photon" hypotheses, to explain the
smooth redshift variation with respect to distance/time,
have a number of (surmountable) problems. But, the
generally accepted solution for this smooth variation,
(namely: BigBang), also has many problems.
If you would, could you supply me with your short list, in
links or references, describing why you may or may not
support this tired photon thinking? [abridged]
Submitted by slawsone"AT"ispchannel.com 1/01
There are NO problems with the Big Bang model which I am aware of. Most cosmologists today are concerned with figuring out precisely what sort of Big Bang model we live in (the amount of dark matter, dark energy, expansion rate etc.), how galaxies etc. formed in detail, and what sort of physics led to the expansion in the first place. There are many discussions about how some specific model ("standard Cold Dark Matter") may not be a good fit, but cosmologists moved on a long time ago from discussing the old alternatives to the Big Bang. The standard cosmological picture fits an extraordinarily wide range of different sorts of data and fits them with stunning success.
One alternative which was discussed from the 1920's and last considered seriously perhaps in the 1960s, was that redshits of galaxies might not be caused by expansion of the Universe, but by some new physical process which somehow causes the light to lose energy on its way to us. This concept fails a number of very simple tests, the simplest being the surface brightness of galaxies. If you are interested you can read a 1991 application of that test in a paper by Sandage & Perelmuter, in the Astrophysical Journal, volume 370, page 455. It is also extremely unclear where the CMB would come from in such a model, how we are to understand absorption clouds along the line of sight to distant quasars, and how to explain estimates of higher temperatures for the CMB at moderate redshifts, to mention a few other examples.
Do you know anything about cosmic radiation and the effect on airline
passengers? I'm particularly interested in the effect on babies, as I
want to take my 4 month old daughter on a 3-hour international flight.
[abridged]
Submitted by kirsten.f"AT"start.com.au 2/01
Let me repeat (again!) that there is a big difference between Cosmic Rays (high energy particles from space, which are the subject of this question) and the Cosmic Microwave Background (very low energy photons produced in the early Universe, which is the subject of these web-pages).
I am not an expert on Cosmic Rays. Although I'm sure that a single short flight is unlikely to expose them to an increased enough level of cosmic rays to be harmful. Some Q&A information can be found at this Pierre Auger Project page, for example. There's an answer to a very similar question to at this this Straight Dope page.
I recently read an article about small particles which travel through the
atmosphere at such speed that they actually pass through us. I don't think
this has anything to do with microwaves but wondered if you could tell me
what they are called.
Submitted PatB"AT"avi.co.za 2/01
There are actually lots of different particles passing through you all the time!
One likely candidate is whatever kind of particle might make up much of the dark matter of the Universe. Those particles are presumably whizzing around the Galaxy and pass through the Earth at high speed with almost no interactions with other particles they meet on the way. But of course this is all hypothetical, since we currently have little evidence for what the dark matter might be made of (although lots of evidence for its existence).
A concrete example of particles which are passing through you all the time are the Cosmic Rays. I've talked about these a little before - they are high energy and cover a range of particle types (protons, electrons, muons, positrons, heavier nuclei, etc.). We are protected from many of them by the shielding effect of the Earth's atmosphere. Nevertheless there are many passing through you every second. And occasionally they will even interact with nuclei of atoms in your body.
Another particle which travels at very high speeds (actually the speed of light!) are the photons. The CMB photons, coming from all directions, amount to about 30,000 particles crossing a square meter per second. Most of them get through the atmosphere and therefore many thousands pass through your body (quite harmlessly) every second.
More prevalent by far though are the neutrinos. Since we are so close to the Sun, the local number of neutrinos is dominated by the solar ones. These amount to something like 1015 neutrinos passing through you every second! And neutrinos interact so weakly that you needn't worry they're doing anything to you in the process - almost all of them pass straight through the Earth without interacting too!
The antimatter asymmetry had its roots at the end of Grand
Unification. That means that after that there wouldn't be any extra
antimatter kicking around, so that things like Mesons wouldn't be able to
form. So is there only regular particles like the quarks and leptons, etc,
so that they can't anihilate or produce mesons?
Submitted by zemmy"AT"paralynx.com 3/01
This is a somewhat technical question, and I'm not really a particle physics expert, but let me tell you how I think things went in the simple Big Bang picture.
As we go further and further back in time, to higher and higher energy, the various quarks will be produced, starting with the lightest ones and then the heaviest ones at the highest energies (earliest times). So now let's start at early times and work forward in time, with the energy getting lower and lower. Top and anti-top quarks, bottom and anti-bottom quarks, and charm and anti-charm quarks annihilated one after the other. And all of these annihilated before the "quark-hadron phase transition". This happened about 10-6 seconds after the Big Bang. Before then quarks could exists freely, while after that point they are "confined" to live in hadrons (groups of 3 making up baryons, or quark/anti-quark pairs in mesons). This is the first time that there have really been bound state of quarks in the Universe. But certainly at this point there are free mesons. At about 10-5 seconds the strange and anti-strange quarks annihilate, along with any baryons or mesons with strange quarks. This leaves just the pions (made of up and down quarks and anti-quarks) and the neutrons and protons (groups of three up and down quarks). But almost right after that the pions also annihilate as the temperature drops below their rest mass. And so after about 10-5 seconds there are no mesons (pions or any other types) left in thermal equilibrium with the other particles, which are just protons, neutrons, electrons, positrons, neutrinos, anti-neutrinos and, of course, photons.
I live in Isfahan,Iran. I like Astronomy and Astrophysics very much.
Will that be possible for you to let me have pictures and articles [abridged]
Submitted by dawod_ast"AT"yahoo.com 11/01
There is no shortage of information about Astronomy and Astrophysics on the internet. Astronomy is a "pure science", i.e. it is essentially useless, and has no direct humanitarian or financial consequences! People only study it for the sheer fascination they have to understand the Universe in which we live. As a result most new research information is quickly made freely available. It is also easy to obtain images from major telescopes, such as the Hubble Space Telescope. Such images are generally usable for any educational, recreational or other non-commercial purpose.
I suggest you browse around, starting with Yahoo or some search engine, to find sites that particularly appeal to you. And remember that the most reliable information comes from established organizations and unversity research groups. Have fun and keep looking up!
I have heard that you have made a studie of the redshift of quasars and =
found no quantization... [abridged]
Submitted by lars.engdahl"AT"telia.com 12/01
The basis for this question is some claims that the redshifts of quasars are not cosmological in origin, but have some other (mysterious) physical explanation. One of the arguments used is that some quasar redshifts appear to be periodic rather than uniformly distributed. There have been several such periodicities claimed. I have not exhaustively investigated these possibilities, although I did once look into one such claim in some detail. What became clear to me was that the claimed evidence was rather weak to start with, and that it was entirely due to selection biases in the data. So that with better data the effect goes away.
This is generally true of all the arguments which have been suggested for quasars not being at cosmological distances - thay have become weaker with time (or disappeared entirely, to be replaced by entirely new weak arguments!), while the conventional picture has gone from strength to strength. So there is no good reason to doubt that quasars really are incredibly bright beacons at vast distances.
It's also worth remembering that the conventional view is far from being conservative! After all it suggests that each quasar contains a roughly billion solar mass star which is actively tearing apart matter and shooting out jets of material at nearly the speed of light. On top of that the whole Universe is expanding, and we see the most distant quasars when the Universe was only about a tenth of its current age.
Do you know why the term milky way galaxy makes no sense?
Submitted by Yellihe"AT"aol.com 1/02
I'm not sure how to answer this question! I wondered whether it might be some sort of joke, with an answer like "to get to the other side". But then I thought it might be wodering about the tautological aspect of the phrase "Milky Way Galaxy"i, so let me answer that.
The Milky Way is the name given to the band of light which stretches across the sky, and around the beginning of the 20th century was identified with the edge-on view of the flattened system of stars that we live in. Then it was discovered that there were many more of these systems of stars, which were called galaxies. Our own galaxy is sometimes referred to as "The Galaxy" (with a capital G) or "The Milky Way", or sometimes the Milky Way galaxy (to distinguish it from the billions of other galaxies out there).
How did they take this picture, if no one has sent a probe above the
galaxy?
Submitted by markwick"AT"telus.net 4/02
The picture in question can be found here.
You're right that it would take thousands of years to send a probe outside of our Galaxy to take a good picture of it.
In visible light we see light from young stars, gas clouds, etc. in all directions through the plane of the Milky Way. Hence a picture of the sky shows the band of the Milky Way going all the way round. Because of the presence of obscuring dust clouds, we don't actually see more than about 10% of the way to the centre of the Galaxy. Hence we can't tell very easily from an optical image that we are actually on the outskirts of the disk.
However, things are very different in the infra-red. Here we are seeing light emitted by dust (as well as from cool stars, etc.), and the Galaxy is transparent at these wavelengths. So we can see pretty much all the way to the other side. Hence, from our vantage point (about 20,000 light years from the centre) we see the disk puffed up towards the centre, with its characteristic bulge. The image looks remarkably like an image of our Galaxy taken from outside it. And that's because in infra-red light we can see that we really are pretty far out from the middle. So in a sense this is an image from outside our Galaxy!
my question is about microwave oven. i want to know who invented microwave
oven?
Submitted by NashatarWindow98"AT"aol.com 4/02
This is not a page about microwave ovens, cosmic or otherwise!
The answer is Percey Spencer, working for the Raytheon company. This application of microwaves grew out of work on radar just after the second world war. Just as detectors for astronomical microwaves did, which led to the detection of the CMB.
Let me add that it would have been less effort to type "microwave oven inventor" into a search engine as it was to send me an e-mail!
photons have no mass but they do have energy.
Using Einstein's E=mc^2, an energy corresponds to a mass.
So please help me putting those things together.
Submitted by 5/02
That simple formula of Einstein's really says that mass can be considered as another form of energy, not that mass and energy are the same thing.
I can take a photon of a given energy and convert it into a particle (at rest) of mass m given by that formula (actually I have to take 2 photons and convert them into a particle and an anti-particle).
Photons have no mass, although they carry energy and momentum. You can't stop a photon to measure how massive it is, since it always moves at the speed of light. That's the definition of a photon, if you like.
We are trying to determine the measurements of planets from the
Sun and each other within our Solar System. Is there a formula or
equation that can be used and also is there a way that we can convert
this to light years?
Submitted by charrison33"AT"juno.com 5/02
I've been trying to think of something relatively straightforward that you could do.
It may help to go back in history hundreds of years to when the scale of the solar system was first being worked out, and use Kelper's Laws. In particular the third law is that the square of the period of an orbit is proportional to the cube of the radius of the orbit. If you use Earth-Sun units, then this is just P2=R3 (where P is in years and R for the Earth-Sun is 1).
Assuming that the planets move in circles, and using this law (which can be easily derived using Newton's gravitational force law, and balancing gravitational forces with centrifugal ones), then if you can estimate the period of a planet's orbit you can get its distance from the Sun. So if I watched Venus for a month, say, so I could guess how long it would take to go all the way round the sky, then I could estimate P for Venus, and hence get R for Venus.
In principle you could make observations to estimate P for all the solar system planets and hence determine R for each of them. But the R's would still be in Earth-Sun units. In other words you could scale your "model" of the solar system by any constant and it would still work. So you need to make one observation of the distance in "real" units. This can be done in a number of approximate ways, and the most accurate ways are to bounce laser light or radar off nearby planets.
If you were to use this method, then the time in years that a signal takes to bounce off, say, Venus and return, is equal to twice the distance in light years.
The Sun does not give off its radiation uniformly in all directions into
space. Why does the sun not give off radiation uniformly all through the
solar system?
Submitted by kojack"AT"codenet.net 12/02
I confess to not entrely understanding this question! The Sun does indeed give off radiation in all directions (although of course the intensity drops off like distance squared from the Sun). The Sun isn't quite a sphere, but it's pretty close, and so there will be a very small correction to this "isotropy". The solar wind and related phenomena are not radiation, nvolve magnetic fields, and are more complicated. But the radiation itself is pretty darned isotropic.
A related question (and one with some relevance to the CMB) is: how far would you have to get from the Sun before the energy flux s about equal to that from the CMB?
I can find nothing yet that states whether the galaxies move clockwise
or anti-clockwise. Can you advise please?
Submitted by tania_lenton"AT"hotmail.com 01/03
This depends whether you're looking at them from the top or the bottom! Since there's no "up" in space, then there's no way to define "clockwise".
During Orbital motional of planets, they are moving at constant speed under the
gravitational force between them and sun. There has to be some extra force
acting on planets which keeps them in constant velocity and prevents them from
falling into sun as apple fail from the tree. I know the velocity of the
planets gen erates the centrifugal force which balances the centripetal force
generated by gravitational force. What force gives this constant velocity to
planets.
Submitted by maple1"AT"vsnl.com 02/03
I believe that you should read an introductory physics textbook about Newton's laws of motion. There is no force needed to keep something in uniform motion. A "force" is precisely the thing which stops bodies from moving at a constant velocity.
Planets in orbit, or galaxies interacting with their neighbours are experiencing the gravitational force, which leads to an acceleration towards the local centre of mass. If they have enough sideways speed (unchanged by a perpendicular force) they continue to accelerate towards the centre, but "miss". This means they continue to be accelerating, but have a sideways motion which keeps them in orbit. It was Newton's realisation that this is what an orbit is which led him (as I understand it anyway, but I'm not a science historian!) to make the connection between apples and planetary bodies.
Is it possible that the black holes are the anti-matter that we are looking
for? The annihilation would absorb all lights and that's the reason we are
unable to see them.
Submitted by RS2DS2"AT"aol.com 02/03
I think you may be confusing "anti-matter" with "dark matter". Assuming this to be the case, can the dark matter by black holes? This question has been considered in some detail. There are quite strict limits on the fraction of the dark matter that can be in black holes of various masses. Very heavy black holes would mess up the structures of galaxies for example, while planet-size black holes would give effects from their gravitational lensing which would have been seen.
It's just about possible for there to be a population of very low mass black holes distributed everywhere throughout the Universe. However, the ideas for trying to form such black holes in the very early Universe are not very promising. Hence most astronomers don't regard such black holes as very likely candidates. But I think it's fair to say that they cannot be ruled out entirely.
Now, no one can possibly answer to these coments here, but I believe
that we aren't capable of understanding how existance came into being. I
believe that we were desingned not to be able to, just as we can not make a
machine that relies on its' own energy. [abridged]
Submitted by Tayjaysap"AT"aol.com 02/03
It is of course entirely possible that we will never fully understand where everything in the Universe came from! However it is certainly the case that our current level of understanding of the early Universe goes well beyond where previoius generations of scientists imagined would be possible. Yesterday's "metaphysics" has turned out to be today's verifiable physics, so who knows where this will lead? We currently have a very robust picture of how the Universe has been evolving since the first small fraction of a second, based on well tested physical theories. And from detailed cosmological observations we have a pretty good description of the Universe we live in, and how it has been changing over billions of years. So at the moment it's anyone's guess as to whether we will ever come to an "ultimate understanding" or whether we'll reach some sort of intellectual impasse.
Until proven otherwise, the working assumption is that there is an ever deeper level of understanding to be discovered. And you can bet that cosmologists and theoretical physicists are having a lot of fun in the meantime figuring out just how far we can go!
If there were such a thing as a neutrino
spectrograph, I gather it would it show that neutrinos from distant
galaxies are redshifted like photons are. Since neutrinos have mass how
would their energy be shed?
Submitted by erckjcbsen"AT"att.net 03/03
In fact there are neutrino spectrographs! It's just hard to detect neutrinos, so at the moment we don't have any obvious sources other than the Sun. But certainly for the Sun you can distinguish the energy of many of the neutrinos that are detected. And it may also be possible to do this for any nearby supernovae which go off. So perhaps some day it will be routine to see spectral lines in neutrino spectra from distant galaxies, and confirm that they are redshifted.
To answer the second part of your question, although neutrinos do appear to have mass, these masses are very small, and so the neutrinos behave essentially in the same way as photons. In other words they are highly "relativistic" particles, meaning that they move at near to the speed of light. So the momentum and energy of a neutrino are related pretty much like they are for photons. Hence you can think of them losing energy to redshift in just the same way that photons lose energy to the expansion of the Universe.
Does the universe expands at the same
velocity as the light? I suppose so, as the expanding
light (EM radiation) is what defines the Universe.
Submitted by amrespi2000"AT"yahoo.es 03/03
The Universe doesn't expand at a constant speed, but at a certain speed per unit length (determined by the Hubble constant, which is slowly varying with time). So, nearby parts of the Universe are expanding away from us at a slow speed, while things which are far enough away from us are expanding faster than the speed of light (and hence we can't see them).
Is the energy density of the vacuum the same as zero point energy from
quantum mechanics?
Submitted by atabeygi"AT"interchange.ubc.ca 04/03
These concepts are certainly very strongly related. The "zero point energy" usually means the energy (associated with the uncertainty principle) which an ideal oscillator has even at zero temperature. It is a very real phenomenon, with many measurable effects.
In "quantum field theory" one imagines space filled with virtual oscillators at every imaginable frequency. So a simple calculation shows that the energy density of empty space should be infinite! The fact that this is manifestly incorrect is one of the greatest mysteries of modern physics. And the fact that the energy density of the vacuum has a small but measurable value (the cosmological constant) is something which many theoreticians are searching for a good way to explain.
My question is, can electromagnetic
radiation escape a black hole? I know visible light cannot but how about
other wavelengths in the electromagnetic spectrum?
Submitted by cdaska"AT"earthlink.net 08/03
There's fundamentally no difference between visible light and other wavelengths of electromagnetic radiation. So, no, they can't escape from a black hole either.
Except for the complicationof "Hawking Radiation", a quantum mechanics effect through which mini-black holes could evaporate.
I was wondering if anyone an idea what would happen if you starve a Black
Hole of matter, then some how erased the effects of gravity on it. Would any
of the matter ingested previously come back with a bang or would it be
simply gone?
Submitted by kgarner"AT"sasktel.net 09/03
I confess that I don't fully understand this question.
But there's a related question about what happens to the information content of a black hole if it evaporates. The puzzle requires that you understand at least 3 things. The first one is that black holes can lose energy (and hence mass) through "Hawking radiation", which is incredibly slow for high mass black holes, but gets faster as the mass of the black hole goes down. The second point is that "black holes have no hair", meaning that every black hole of the same mass (and charge and spin) is exactly the same as every other, irrespective of what it was made of. So the information about what made the black hole is entirely contained within its horizon. And the final thing to understand is that information is related to entropy, which isn't normal allowed to decrease.
So what happens to the information when a black hole evaporates entirely? It turns out that this is still a big puzzle for theoretical physicists.
could you explain to me, why light travels in a straight line please.
Submitted by Aambourne"AT"aol.com 09/03
One of Newton's Laws of Motion is that things travel in a straight line unless some force acts on them. So light moving through free space travels in a straight line.
You can apparently bend light around massive objects - it's called "gravitational lensing" and is commonly observed for distant objects in the Universe. But one of the fundamental principles of General Relativity (the most complete theory of gravity that we have) is that light still travels in a straight line, it's just that space itself is curved. This turns out to be both a deeper description of what's going on, and a more accurate one. So light always travels in a stright line, it's just that straight lines look bent!
if you could produce a magnetic field large enough and
strong enough, what would happen to the electron as it neared the speed
of light? The second part of the question is if the electron continued
of it's circlular path, would the energy required to produce the
centripital acceleration be greater than E=mc2? How can this be?
Submitted by cheer2002"AT"hotmail.com 09/03
Let me start by saying that this is not a subject on which I am an expert. But this is exactly what particle accelerators do every day - so you can probably find out more by looking for information at the web-sites of places like CERN or Fermilab.
However, the short answer to your question is that the electron starts behaving "relativistically", i.e. you need ideas of Special Relativity to understand what's happening as the electron gains more and more energy. Certainly the total energy can be much larger than the equivalent of the electron's rest mass. But it gets harder and harder to increase the speed as it approaches the speed of light. On top of that an electron circulating in a magnetic field will also radiate, and the energy lost in this way makes it even harder to accelerate particles to the highest energies.
Does the fact--one last stab at the key to the mystery-
-that 15 B years ago everything was much closer together have
anything to do with the fact that from any point in the current
cosmos one would be observing as if from the center?
Submitted by steveg"AT"spa.net 12/03
The best way to understand the "no centre of the Universe" thing is to do the following exercise with 2 overhead transparancies. Cover one transparency with a random pattern of dots using some colour. Then take it to a photocopier with a zoom function and copy it on to the other transparency at something like 110% enlargement. Then you can project the two images together, lining up some particular dot. You should see that all the pairs of dots appear to move away from the dot you chose.
But if you choose another dot as your "centre" and repeat the exercise, then you should see that all the dots appear to be moving away from that one too! In other words all of the dots are equally valid centres for the expansion, and it just depends on your point of view. So it is better to say "everyone is the centre" of the Universe" rather than "there is no centre of the Universe"!
What you've done is show that uniform expansion looks like recession of everything away from everything else. An even better way to demonstrate this is by making measurements on your transparencies. Get out a ruler and measure the separation between some chosen dot and a bunch of others, and do this on each transparency. The speed at which things are moving away (or in this case the distance apart on the second image minus the first, divided by some fixed time interval between these two "snapshots") is proportional to the distance - in fact it's just equal to 10% of the distance if you enlarged by 110%. But this recession velocity doesn't depend on which dot you chose as the "central" one in the first place. You have just proved that Hubble's Law (recession speed proportional to distance) is exactly the same thing as uniform expansion!
Because, as
you have indicated in previous answers, we are in a pretty normal galaxy in
a small cluster of galaxies- why wouldn't life have formed other places? One
only needs to see the deep field pictures to realize how many galaxies there
really are. Also, do you think different techniques will soon confirm the
existence of life outside of the solar system?
Submitted by lisaacson123"AT"earthlink.net 04/04
I am not an expert on this topic. But let that not stop me giving you an answer!
There are a range of opinions about the likelihood of life elsewhere. To me (and you I gather) it seems pretty amazing to imagine that our little corner of the Universe could be the only one to harbour life. But to some people, the emergence of life seems so unlikely, that they imagine that it might only have happened once.
The exciting thing is, now we know there are planets around some other stars, that there are direct observational ways of finding potential signatures of life on those planets. This may still be a long way off, but it's no longer science fiction!
I'd like to access more
of the files you have available on it, but for some reason I can't open the
files with extension '.ps' and for all my worth I can't find out which
application runs these files.
Those would be "postscript" files, which is a common format in the physical sciences. You need something like "ghostscript" to view them (depending on your operating system).
Why is the cosmic radiation that hits Canada more intense than that which
hits Mexico?
Submitted by robmiller"AT"hawaii.com 04/04
This is a question about Cosmic Rays (i.e. high energy particles hitting the Earth from space), rather than the Cosmic Microwave Background (i.e. low energy photons generated in the very early Universe). I may claim to be an expert on the latter topic, but not the former, sorry!
Having, said that, there is clearly a latitude dependence in the amount of cosmic rays reaching the ground, because of the Earth's magnetic field (which in fact protects us from most of the cosmic rays). You can check out the official Canadian word on this topic here.
I would appreciate if you could answer this:
Would living in a residential compound too close to
the microwave/communication tower be harmful to one's
health? Some people say it could affect your health if
you live nearby this facility for a period of time.
Submitted by jeremiah012556"AT"yahoo.com 06/04
This is a topic on which I am not an expert. However, common sense would suggest that there are enormously more significant health risks in your life than some weak radio or microwave emissions. So I personally would not worry about living near a microwave tower (of course you probably don't want to stand directly in front of a transmitting dish for too long). However, the exact amounts of low-level electromagnetic radiation required to have any noticeable effects on someone's health are not really known. But I do know that the Cosmic Microwave Background, which is passing through us all the time, has no effect whatsoever!
You might try looking up the answer on other web-sites such as this, and other things you can probably find easily. However, I should caution that much of what you find on people's web-pages (as I just discovered when I did this exercise) is quite alarmist and ill-informed!
-we had this argument at the office
-what is the life span of the sun
-when will it end
-what will happen to old sun and will there be a new sun or some other
planet will come along and act like a sun
-please advise
Submitted by ben"AT"oayec.org 08/05
Based on the current properties of the Sun in comparison with models of stella structure and evolution, which have been staggeringly successful at explaining observations of other stars, we have a pretty clear idea of the Sun's future. Right now the Sun is about half-way through its natural life. So in about 5 billion years it will start to run out of its main fuel source (hydrogen in the core, which is being converted into helium through nuclear fusion). It will then become a red giant, swelling enormously in size and getting much cooler. Depending precisely on how much mass the Sun loses during its life (something the experts argue about), the Earth may or may not be swallowed up. But it will be pretty hot at the Earth's orbit in either case! And shortly after tha (by astronomical timescales at least), the Sun will explode and become a "planetary nebula" with the core cooling as a white dwarf.
So we probably need to figure out a way of moving to some other part of the Galaxy. And we've only got 5 billion years to figure out how to do it!
Plz tell me "what is meant by polarization of proton?"
Submitted by sadia_saadia"AT"hotmail.com 10/05
Protons are sub-atomic particles, which have a property called "spin", in analogy with the spin of macroscopic partciles. The spins of a bunch of protons can be aligned, or not, and this is what polarization means. For more on proton polarization you could try the web-page of the news article.
Photons, on the other hand, are particles of the electro-magnetic field, the oldest of which formed about 13 billion years ago, which we can detect today as the Cosmic Microwave Background. The CMB is slightly polarized, meaning that the photons arriving have their (say) electric fields oscillating more in one plane than another.
For information on polarization in general, you might like to try the Wikipedia article.
How do i put a picture from my PC to become my website background ???
Submitted by sexytom_felton"AT"hotmail.com 10/05
OK, so this takes the prize for the least relevant question that has ever been sent to me!
I want to know why a hot body will emit em wave (mainly infrared). Is it
because the electrons in the hot body lose energy and the energy is in the
form of em wave?
Submitted by nc_leung"AT"hotmail.com 10/05
This is an excellent question!
Thinking along these lines was what led Planck and others to come up with the basics of quantum mechanics in the early 20th century!
You're right that this is to do with electromagnetism and with the energies of particles. But, the classical (i.e. pre-quantum mechanics) theory of electromagnetism, combined with statistical mechanics doesn't fully explain the blackbody emission spectrum (it would predict too much emission at high frequencies). The addition of the idea that radiation comes in quanta is what allowed physicists to finally explain the blackbody function.
The basic principle is that anything with a temperature has "motion energy" associated with its particles, and that this energy is converted to photons (through the osillations of charges). The characteristic energy of the photons depends only on the temperature of the matter (assuming it is in an equilibrium situation), with a spread of energies given off, according to the mathematical blackbody function.
That's what your body does, with a peak wavelength in the infrared part of the spectrum. And that's what the early Universe did, with a peak wavelength in the high-energy part of the electromagnetic spectrum, but redshifted by the expnading Universe so that we observe it today as the Cosmic Microwave Background.
Hello, I am an astrophysics student, I was hoping you could help me with
a question I am having difficulty with solving..
The question is consider a star like the Sun falling towards a
supermassive black hole in the centre of a galaxy. At some point, the
star will start to be torn apart, for what black hole mass (MBH,crit)
does this happen at the event horizon? Would you except to observe
anything from such events for black holes with masses above or below this
limit?
Submitted by sweet_and_joyful11"AT"hotmail.com 09/07
There are 3 answers to this question.
A: I make it a rule not to do student's homework for them.
B: I'm not really an expert on black holes.
C: The answer is pretty simple in any case!
Light ( and other forms of energy) interact with matter in various known
ways. Light also travels through 4-dimensional spacetime according to
principles of General Relativity (which I confess to have read very
casually). What I am wondering about is that after leaving its source and
travelling through spacetime, can ( or does) light exactly retrace its path
through spacetime? Spontaneously?
Submitted by docgsb"AT"telus.net 09/07
I'm afraid I don't follow what is being asked here.
Light is emitted by matter - whether it's stars, flashlights or even bits of the early Universe (that we see as the CMB). It travels outwards from the emitting object at the speed of light and often (but not always of course, e.g. the flashlight!) in all directions. It goes in straight lines, unless it travels through a place where space is curved by a concentration of mass.
Light doesn't retrace its path, unless of course you put a mirror in its way! And it doesn't really "travel through 4-dimensional spacetime", it just travels through space at the speed of light.
Maybe you're trying to make things more complicated than they really are?
In the 4th chapter titled 'The Relation of the Four Co-ordinates to
Measurement in Space and Time' in the section A titled Fundamental
Cosiderations on the Postulates of Relativity', Albert Einstein's
calculations showed that if the ds belonging to the element dX1....cX4 is
positive, we follow Minkowski in calling it time-like; if negative, we call
it space-like.
In the introduction by Richard Price in the book 'The Future of Spacetime';
it was explained that, in the Minkowski spacetime, a 45-degree worldline
would be moving at the speed of light c. Is this cut-off the same as the
positive and negative for the ds above?
If so, I am wondering whether
whether it would still reconcile with Albert
Einstein's calculations (all Greek to me) if it was proposed
that worldlines right of the
above-mentioned 45-degree cut-off were to be considered 'blackhole-like' and
those to the left, in turn, were considered 'time-like' if I were to
hypothetize that, in stead of 4-dimensional spacetime, time is
three-dimensional and blackholes are forms of densely packed time
concentrations (time banks).
Submitted by docgsb"AT"telus.net 11/07
I remember reading that old book of Einstein's when I was in High School, and finding it surprisingly readable - even if there were a few technical parts that I didn't fully understand! So I agree that this is still a good place to start trying to understand relativity. There are of course lots of other books on that subject. The trick is to find the one at just the right level for you, so that it pushes your understanding a bit deeper.
I think you already have some of the right ideas though.
In this language "ds2=0" represents events separated by the speed of light, which are 45 degree lines on a "space-time diagram". Black holes can be thought of as regions of space which are only connected to ordinary parts of space by lines that would be steeper than 45 degrees, i.e. you'd have to go faster than the speed of light to get out of the black hole region. I'm not sure if that's equivalent to what you say at the end of your question.
I'm trying to understand the following, an electron has mirror image ,the
positron or anti electron which are the same in every way accept their
charge is deferent.The same applies to mater and anti mater we can have
Galaxy's of mater ore anti mater which will behave in a mirror image.
My Question is about gravity, Why is the speed of gravity 300000 km/s
and anti gravity is aloud to have speeds which are many times the speed
of light. The Question is asked in relation to inflation.
Submitted by nickst"AT"tpg.com.au 03/08
A positron is the anti-matter version of an electron. The "mirror image" thing is an analogy - anti-matter isn't literally the mirror-image of matter, it's just that the particles have opposite properties, like charge, spin, etc.
It doesn't look like there are appreciable quantities of anti-matter anywhere in the Universe, even although individual particles of anti-matter are being created (and annihilated) all the time. So it's incredibly unlikely that there are any anti-galaxies. In fact the observation that our Universe is dominated by matter, rather than being half matter and half anti-matter, is one of the big puzzles of early Universe physics.
Matter and anti-matter both have positive mass and energy. And all particles with mass experience the gravitational force, which is not an instantaneous force, but travels (if you like to put it that way) at the speed of light.
What is the ratio of supernova explosions per galaxy's,in
Galaxy's 3.75 Gly from the Big Bang to Galaxy's in our group of
Galaxy's.is there data available to answer my Question
Submitted by nickst"AT"tpg.com.au 03/08
This is the sort of thing that astronomers are just now trying to understand. It's related to the general problem of determining the star formation history of the Universe. This is because some kinds of supernovae (usually called "Type II") come from the most massive and short-lived stars, and so estimating the rates of these supernovae allows you to estimate the total rate of star formation (or vice versa of course). But finding supernovae in the most distant galaxies is difficult, and so right now our knowledge of these early times is is pretty sketchy.
If the anti-particles and matter particles annihilated each other for the
last time and by some asymmetry some more matter particles were present
that resulted in the formation of the modern day galaxies,where does the
anti-particles come into existence now?as they must have been annihilated
in the early universe,otherwise they would not allow matter to be formed
if they were present to this very day..
Unless some barrier results in their isolation from the matter
particles.Could u please solve this analogy?
Submitted by resurrection_mastermind"AT"yahoo.co.in 11/08
You can make particle/anti-particle pairs out of pure energy. You basically just need to make enough energy in a small enough volume. You can also make some anti-matter particles when you smash up atomic nuclei. So this happens in space when cosmic ray particles hit each other, and it also happens in nuclear reactors and particle accelerators.
So there are some anti-particles existing today, but this is small potatoes compared with conditions in the early Universe.
Today there are (on average) about a billion CMB photons for every atom in the Universe. At very early times there were about equal numbers of particles, anti-particles and photons. The vast majority of the particles annihilated with the anti-particles to make a bunch more photons, and leave the Universe with lots more photons than atoms.
why is it you can see the stars by day if you look at the water level at the
bottom of a well?if you don't believe me try it.
Submitted by info"AT"drnabilhassan.org.uk 11/08
Although this is a fairly persistent claim, it is unfortunately completely mythical. And if you don't believe me, then by all means try it yourself!
The difficulty in seeing stars in the daytime is caused by the brightness of the sky, which comes from sunlight scattered by the atmosphere. Blocking the direct light from the Sun doesn't make any difference. From down a deep well you see a small patch of the sky, but that patch is bright and blue (or white of course) just as that same patch would look if you weren't down the well.
When particles are speeded up to relativistic velocities,
does their gravity increase when their mass does?
Submitted by werle@att.com 01/09
The short answer is "no".
In fact the mass of a particles doesn't really increase as it speeds up. Although this is sometimes stated in popular descriptions of special relativity (and even some technical ones) it's just not a helpful way to describe things. That's because it leads to misleading lines of questioning like yours!
When a massive object speeds up, its rest mass stays the same, because the rest mass is a property of the object, and not how fast it's moving. However, the momentum and kinetic energy of a particle do change, and they change in a way which is different as you approach the speed of light. Sometimes this is described as the mass increasing, so that the momentum (for example) looks just like mass × speed. But really it's that the momentum in special relativity has an extra velocity-dependent part. And if you try to "shoe-horn" it into Newtonian mechanics you just get yourself confused.
So the gravitational effect doesn't really change as a particle speeds up.
Of course there can be more subtle effects. For example, you have to ask the question of when the relativistic particle feels the force, because in relativity the gravitational effect can only travel as fast as the speed of light. And if you have a "gas" of relativistic particles, then the pressure also acts as a source of gravity. To do these things properly you have to calculate things within General Relativity.
My question this time is, of the dimensional unit of expansion
Ho=2.225736445^-18 %of a cm ,m,Km per/s Mps^-1e
which can be derived by G/c. and G/c is my creation by accident then by
intention [abridged]
Submitted by nickst"AT"tpg.com.au 03/09
The dimensions of H0 are 1/Time, and so although the conventional units are km/s/Mpc, this can be reduced to just "per second" by converting Mpc to km (or vice versa).
The dimensions of the gravitational constant G are Length3/Mass/Time2 and if G is divided by the speed of light, c, then the dimensions are Length2/Mass/Time. The units of G/c are therefore m2/kg/s.
So the dimensions of H0 and G/c are not the same (or equivalently, they can't be converted into the same units).
So the coincidence between these quantities, using a particular choice of units, can have no physical meaning. It's like saying (for example) that your age in years is equal to your height in feet times your weight in stones (a British unit, equal to 14 pounds). That would just be a coincidence, since it wouldn't be true if you chose to use seconds, metres and kilograms (or any other random choice of units). Only dimensionless ratios of quantities have physical meaning - or in other words you can only compare quantities which are dimensionally the same.
Ibm an electronics technician, and in the later half of the last century
(1991) it is claimed that Roland De Witte detected absolute motion of the
earth through space.
http://www.ptep-online.com/index_files/2006/PP-06-11.PDF
less formal version:
http://www.teslaphysics.com/Chapters/Chapter160-DeWitte.htm
Do you have any take on that, and also- is sidereal time related to the CMB?
Submitted by servicetech"AT"navair.com 06/09
I've tried to read this paper. I should be blunt and state up front that I don't take it at all seriously. It seems like so many other pieces of fringe science - poorly written, badly researched, not published in a formal peer-reviewed journal, difficult to understand, full of self-citation, etc. These are all the sorts of things which are hallmarks of what has been called the "pottery magician", i.e. something which masquerades as science, but really isn't. The internet is full of such stuff. Fortunately it's usually easy to distinguish it from a careful scientific study, because it typically so poorly written!
Sorry that I'm not mincing words here.
I should point out that de Witte seems to have never published his results himself. Instead we have a report on his experiment by someone else. The journal it appears in looks like it was set up by a group of other people on the fringes in order to promote their own stuff (i.e. the editorial board and the list of authors are strikingly similar). The paper doesn't mention the huge amount of mainstream work which followed the Michelson-Morley experiment (which was more than a century ago!), but instead cites either very old studies or the author's own work. I could go on.
The fact that the physics makes no sense to me is hardly surprising after all the flags tell me this is not a serious study.
I don't know of any connection between sidereal time and the CMB. But the CMB itself points to the fact that there's no such thing as an "absolute rest frame". The CMB "dipole" (one side of the sky being hotter than the other because of our motion) tells us that the Earth is moving "through the CMB photons" at about 600 km/s. This is much bigger than the Earth's motion round the Sun (the focus of the Michelson-Morley experiment and others). In fact you can see the annual variation in the CMB dipole caused by the fact that the Earth's velocity vector changes direction (relative to the CMB frame) throughout the year. And you can even see the daily modulation of the CMB dipole if you have an experiment on the spinning Earth. What you realise is that there can be no special reference frame, otherwise the CMB dipole would make no sense.
We know the established equation, p=-rho. But pressure and density have no
direction. So, which one is negative?
Submitted by bd_abdussamad"AT"yahoo.com 01/10
I don't really understand the question, since "direction" isn't involved here. Energy density (just like mass density) can only be positive. Pressure is also positive for all normal kinds of stuff, i.e. "matter" and "radiation". However, in principle there's nothing to stop pressure being negative, and indeed it turns out that for vacuum energy it is maximally negative, with a magnitude equalt to its energy density.
So is positive and P is negative for Dark
Energy.
I am a citizen interested in physics and "dark matter" theories.
I have been searching for a possible explanation for these phenomena.
While I have at various times come up with several possible explanations,
unfortunately I don't have access to enough raw experimental data to test
these predictions to see if they are consistent with existing experiments
and to develop and formalize mathematical models.
I was wondering if there is any way I could get access to data collected
from various experiments, and how to go about downloading data for automated
analysis by computer programs? I would love to try attempting to solve the
dark matter/dark energy problems, even if ultimately I don't find the solution.
Submitted by exaeta"AT"protonmail.com 03/19
In fact a lot of data from astronomical surveys is available online. That's because it's common in astronomy to make data public (even if that's not true in all areas of science). So you really just need to figure out what data you are interested in and then go and look for it on the internet.
I should warn you that of course it's not that simple in practice. First of all some of the data sets can be quite large. But secondly, you tend to need to know a lot about how the data were taken, in order to properly use those data. That means that there's no substitute for reading the original published papers in detail, so that you can understand the nature and limitations of the data.
Good luck!
I am currently doing a project on black holes and the second part of this
project is to reach out to an expert on it. I have a few questions that I am
hoping that you can answer for me.
What first got you interested in black holes or just space science in general?
What do you find most interesting about black holes or just space science in
general?
How does a black hole form?
Are black holes "doorways" to other parts of the universe?
Submitted by austinbai9187"AT"@gmail.com 12/19
Everyone who knows a little about black holes finds them fascinating - they are places where physics is quite extreme compared with the everyday world of humans, and hence there are many weird and wonderful phenomena.
I'm not sure what first got me interested in pursuing astrophysics - but I certainly have never regreted it, since I can't think of anything more interesting to do for a living than to study the Universe!
Perhaps the most amazing thing about black holes is that we have good evidence that they actually exist!
There are two distinct kinds of black holes. Those that are around 10 times the mass of our Sun and undoubtedly formed from the deaths of high-mass stars. The second type are "supermassive" black holes, which are millions to billions of times the mass of the Sun. We don't currently know how they form.
Are they doorways to "worm-holes" or something like that - probably not! I would say that real black holes are interesting enough that we don't need to invent extra properties from science fiction for them to have!
I read a book recently by an Australian physicist who claims that all theories
and hypotheses that attempt to explain the apparent "fine-tuning" of the
universe, fall short. According to him, the best explanation is that the
fine-tuning is the result of a Creator or Higher Intelligence.
May I please ask for your opinion as a physicist on why the universe seems
to be fine-tuned? Postulating a Creator just seems to replace complexity with
something more complex.
Submitted by pjwlouw"AT"gmail.com 04/20
I usually try to avoid discussing religion, since it's not something that I'm an expert on. So let me only comment on the science part of this question. The phrase "fine-tuning" means different things to different people. If you're talking about the physics that defines the Universe, then such a discussion pre-supposes that the Universe could have turned out differently, which essentially means that you're proposing a set of possible universe, i.e. a multiverse.
This means that you're really talking about aspects of the so-called anthropic principle. This is something that physicists disagree about. There's a broad spectrum of opinion from "this is the most profound idea that we can think about, and might lead us to understand why everything is the way that it is" to "this is the stupidest thing I've ever heard of, and I don't even think it should be dignified by giving it a name!" It's an entirely reasonable position to take to assume that the Universe is simply the way that it is, with no possibility of being any other way. In that case, "fine-tuning" has no meaning.
If dark matter forms haloes around gravity wells with structure and
gradients would we not be able to infer the effect of these gradients by
using Professor Carlos Franks models to map the solar system and history of
interplanetary probe course corrections?
Submitted by sta6"AT"hotmail.com 09/20
I'm not sure specifically about Carlos Frenk's model that you're referring to. But I think you don't quite have the right idea about the scale of dark matter halos. The dark matter distribution is fairly smooth on the scale of the whole of out Milky Way Galaxy, and very smooth on the scale of the Solar System. Moreover, in the Solar System, the density of non-dark matter (i.e. regular atoms) is much higher, because it's a special part of the Galaxy, containing a star and several planets (rather than the low density of an average part of space). So within the Solar System, there's very little hope of inferring any local effects of dark matter.
I had a philosophical question to ask so I emailed you and other best
cosmologists and neuroscientists in the world. The question is this:
Which scientists know more about the secrets of this world(or which one knows
more whether there's a secret or not)?
Cosmologists as scientists who know lots of things about the existence of this
world and how it has been formed or neuroscientists who know about how we
humans can perceive this world.
Submitted by
They're completely different spheres of knowledge. Cosmologists know more about cosmology and neuroscientists know more about neuroscience.
We are working on a project that works to find a solution to the large amounts
f garbage produced on Earth.
We thought of the solution of launching a missile which contains garbage
in the suns direction.
Our problems are: the amounts of garbage on Earth are very large, flying
the garbage will cost a great deal of money.
So we decided to work together with the group of the venture: air pressure.
We thought of launching the missile with the help of air pressure.
We have some questions: 1. Is it possible to use the missile multiple times
and send new garbage each time?
2. With the amount of garbage on earth, is our venture relevant and possible?
3. Can we compress the garbage to reduce the the amount of space the garbage
takes on the ship?
Submitted by daniellemor100"AT"gmail.com 1/22
I'm not really an expert in this area.
However, let me offer the suggestion that you look into the energetics of the processes that you're thinking about. How much energy might it take to get a certain weight of garbage into space, and then how much additional energy to get it to go directly into the Sun? The physics is all about escape velocities and orbital speeds.
Good luck!
[abridged] I looked deeper into Planck's
constant, and realized it could be understood as
proton mass * proton radius * c * pi/2.
Yet for some reason this knowledge hasn't made its way into the world.
With this in my back pocket, I then realized the fine structure constant
could be understood as
4 * electron mass * electron radius / (proton mass * proton radius).
I think this is important, because this defines the constants in terms of
quantities that map to real phenomena. For example, the proton radius.
What's your take on the decomposition of Planck's constant and the fine
structure constant?
Submitted by Sahil Gupta sahil"AT"spase.io 7/21
Subatomic particles, such as the proton and the electron don't have sizes in the same way as everyday objects, such as the ball used in your favourite sport. However, there are various ways to define some kind of size for such particles, depending on the physics you're considering.
When charged particles interact with electromagnetic radiation they do so over a characteristic scale that comes from considering the electric force. This is called the "classical radius". Since it depends on the charge squared, and with the inverse of the mass, then this radius goes like α/me.
When quantum mechanics is involved, there's another size that can be defined, which is usually called the "Compton wavelength". This is basically Planck's constant divided by the speed of light and the particle's mass, i.e. h/mpc for the proton.
Your descriptions of deriving Planck's constant and the fine-structure constant from the radii of electrons and protons is just rediscovering the relationships that defined these radii in the first place.
Is there any life outside of Earth?
Is it possible for more life to live outside of Earth?
Submitted by ahubn38"AT"lewiscass.net 4/22
Of course no one knows the answer to your first question! Most astronomers would probably bet that there are multiple planets with life, somewhere in the Universe, simply because the Universe is so large. That view has become stronger in the last couple of decades, as we've discovered more and more planets around other stars. So at least we know that planets are very common. And presumably planets that are quit like the Earth aren't that unusual. So now the search is on for evidence of biological activity in the atmospheres of distant planets.
If I understand your second question correctly, then I think the answer is basically the same as for the first one!
I stumbled onto your homepage
and I was wondering what are the job opportunities in Canada for
Astronomy?Submitted by star_diana_tran"AT"hotmail.com
That's a pretty general question, but I'll have a stab at an answer!
Of course the answer all depends on what stage you are at currently, and what you have in mind for your future. To become a professional astronomer (studying the CMB, or anything else) requires a bachelors degree and generally a PhD as well! But there are plenty of jobs related to astronomy which require less training. It's also important to realise that if you choose this career path, there are many possibilities open to you besides simply becoming a professional astronomer. Many people who graduate with degrees in astronomy (or in astronomy with physics, astrophysics, or whatever) go on to jobs in high-tech industries, government labs, computer companies and all sorts of other places. You should think of astrophysics as being an applied physics qualification - you can't get very far in it without a thorough background in physics and maths - and when you finish your education you are as much (or perhaps more) capable of finding a good job as the average physicist.
As far as careers in Canada go, the opportunities are much the same as in other western counties. This may partly be because professional astronomers often find themselves spending some of their careers working in other countries! For more information about astronomy-based careers, you should check out the American Astronomical Society Careers in Astronomy page.
Since I was young, I've been
extremely interested in Science, especially physics, and I hope that I
can one day become
a physicist. I was asked to do a project in which I have to interview a
professional or anyone with the occupation I'm interested in.
I'd like to ask if you could answer some of the questions that
I've arranged in order to gain more insights into your job?
Submitted by maryfang"AT"tieus.com 9/98
This was such a polite and well-phrased e-mail, that I had to oblige! Since it has nothing particularly to do with the CMB, I don't want to clutter up this page with a lengthy answer. But for anyone else who is interested in the sordid details of life as an astrophysicist at a Canadian university, the questions and answers can be found here
I am looking for universities that have programs in cosmology...
I also have one more question, and that is if I
should be trying to study cosmology or not, if
sometimes the details of astronomy can be
boring to me ... ? (abridged)
Submitted by Zillah21"AT"aol.com 4/99
Many people use the label "cosmology", and mean different things by it. This ranges from purely observational cosmology (what is the value of the Hubble constant? how do galaxy properties change with time?) through physical cosmology (fitting models for how structure arose and developed - understanding the CMB, dark matter, etc), to early universe cosmology (inflation, baryogenesis, nucleosynthesis, etc) and ultimately to quantum cosmology (origin of the Universe, and other studies bordering on metaphysics).
It sounds like your interests may lie towards the end, rather than the beginning, of that spectrum. On the other hand, it may be that you have a narrow view of what astronomy is! There is still a perception that astronomers spend their time staring through telescopes and naming stars! In fact almost all professional researchers spend their time studying particular objects, or samples of objects, applying their physics knowledge to understand the conditions in very distant systems. And so it may be much more like physics than you imagine.
The second thing I'd say in favour of "astrophysical cosmology" is that we've only made any real progress in understanding the Universe through observations. Whether it was Hubble's examination of galaxies to discover they are expanding away from us, or Penzias and Wilson's discovery of the CMB radiation, the big conceptual leaps have come about from observations (and I say this as a card carrying theorist!). The reason that cosmology is currently so exciting is that there are a number of observational projects underway (including those studying the CMB) which seem able to allow genuine progress in putting together a more detailed picture of the Universe. And there are theoretical models which are mature enough that they will be discriminated amongst using the new data. If either the theoretical work had hit a dead end, or there was no imminent prospect of vastly better data, then cosmology would not be the feverishly exciting field that it current is!
And now to answer your first question - there are many universities where you can pursue graduate studies in various aspects of cosmology. Probably the best way of finding out what's best for you is through the web. Check out what research is done at some universities that you are already thinking about. To get more ideas you might want to look at who has been writing papers recently on topics that are the most interesting for you. Current preprints of papers can be found at the xxx.lanl.gov archive. Anyone actively working on things you think sound cool could be considered as a potential graduate advisor.
I am currently enrolled as a junior at High School ...
I have been studying Cosmology on my own ...
I was wondering if you knew of anything that I may be able to do either over
the summer or during the school year that may help me further my knowledge of
the subject. [abridged]
Submitted by keithbubba9"AT"aol.com 1/02
I would recommend that you keep reading and studying. Try something a little more challenging, like a college level textbook. And if you want to realistically pursue cosmology later, you're going to have to put in a lot of effort to be good at mathematics and physics.
One other possibility is to try to get some direct experience working over the summer with an astrophysics researcher in your area. Some of the big labs have programmes aimed at high school students (although there is much more for undergraduates of course). You might try looking around for possibilities. If you have a nearby university you might try and offer your services to someone who works in an area of interest to you. If you imporess them that you are very keen, and you can offer to help for free, then it's feasible that someone might be prepared to take you on. From your point of view it will be great experience to help directly with some research project - but obviously from their point of view it has to be clear that you'll be more of a help than a hinderance! Still, it doesn't hurt to try!
1. What drew you to the study of cosmology over other
sub-specialties in physics and astronomy?
2. Did you have a clear set of objectives regarding
your chosen line of research? If so, have you noticed
any change in your primary objective(s) with your
accumulated experience as a researcher?
3. What do you like most about your work environment?
Dislikes?
4. Funding for research seems a perpetual uphill
struggle. In your view/experience are the requirements
for funding a limiting constraint on academic freedom?
Do systematic constraints make it tough for one to
pursue less popular and/or more esoteric areas of
research?
5. Is funding as big of an issue for theoreticians as
it is for experimentalists? (Although, at some point,
the work of both sides must meet, I won't assume that
this scientific fact is reflected in the bureaucracy).
6. I'm curious to know if the undergraduate physics
curriculum has kept abreast with scientific paradigm
shifts. (I'm thinking here about the traditional
treatment of real physical systems as perturbations of
well-behaved exactly solvable ones. In the last twenty
years or so, I believe, more emphasis has been placed
on developing the mathematics of non-linear systems as
a tool to describe the "real world". Has this change
of perspective reached down to math courses for
physics undergrads?)
7. Is there anything you can think of that would be
helpful to me that I've failed to address and that you
think I should know - regarding my look at returning
to academia to pursue a research-science career?
Submitted by henrythehorse1967"AT"yahoo.ca 8/03
Let me try to give brief answers to these: 1. Cosmology is BIG and COOL! 2. I wanted to work in cosmology from the time I first went to university. Precisely what I work on varies over time since there are lots of interesting things to do and I get bored working on the same thing for too long! 3. I like the fact that as an academic I don't really have a boss. I dislike unnecessary paperwork and beaurocracy! 4. Of course I would like more research funding. But in fact the funding which is available enables me to more or less work on what I want. I have never carried out "applied" research and never intend to! 5. Theorists don't usually need as much money as experimentalists. Pencils are cheap! (But of course funding mostly goes on support for students and postdocs, computing equipment and travel). 6. This sort of thinking isn't terribly relevant to the sorts of astrophysics I work on. Undergraduate teaching is always trying to reach a compromise between covering the essential ground-work for what will come later and being up-to-date. 7. You have to work extremely hard to be a successul academic. You will make less money than you might in industry or commerce. But I assume that the job satisfaction is considerably higher!
i want to know if a do my bacherlor's degree in
astronomy, what kind of job i can get and what kind of income range i can
expect.
Submitted by mandeep127"AT"hotmail.com 5/07
There's a new web-page which summarises lots of astronomical career information from the Canadian perspective. It's hosted at the CASCA (Canadian Astronomical Scoiety) web-site, and I've put a link here.
I am Iranian and now I'm 16 years old.
I really appreciate your help if possible please answer my question:
1) What are the requirements to enter in astronomy and astrophysics field?
2) what are the conditions of finding a job in this field after graduation?
3) How can i qualify myself at this age and start preparing myself for studying astronomy? (so that I have a better chance of being accepted)
I've been taking astronomy classes and as a result I have some informations
about basics and fundamentals of astrophysics and cosmology.
Submitted by atoosaomranian"AT"gmail.com> 3/24
To succeed in astronomy and astrophysics, it's important to do well in physics and mathematics courses. Those are probably more important than astronomy courses!
The professional societies of astronomers in many countries have usually studied what careers people go into after a degree in astronomy or astrophysics, and they also provide information about how to pursue a career in astronomy. For example, you might want to look at this page from the American Astronomical Society or this leaflet from the UK Royal Astronomical Society. These will give much more comprehensive answers than I could manage here.
Will you answer my question about the CMB?Maybe. Send e-mail to dscott at my address astro.ubc.ca and see what happens.
Please let me know if you find any errors on this page!
The answers posted on this page are Copyright 1997-2022, Douglas Scott.
Douglas Scott
dscottATastro.ubc.ca
Last revised: 18th March 2024
