
|
Welcome to the Solutions site for Practical Statistics for Astronomers, Second edition (2012). |

|
Welcome to the Solutions site for Practical Statistics for Astronomers, Second edition (2012). |
The exercises in the book span a wide range of difficulty. Some are relatively simple algebraic exercises and others are mini research projects. Many of them are open-ended and involve constructing the right question as well as deducing the right answer. In this respect they are much like the process which goes on in real-life research. The solutions given here, correspondingly, are often not stage-by-stage answers, but rather a set of hints and suggestions, with numbers provided in cases where we have real numerical data available. This is useful for the simulations in particular, as then you can use the same set of random numbers as we did.
We welcome comments and errata, both for the solutions and for the book.
A note on data files: some are in fixed formats, and some are in free-format. The latter do not have any embedded comments so their contents are described in the relevant solution.
You may contact the authors via
jvw@phas.ubc.ca
1.1 At first sight, discovery of a new phenomenon may not read as an experiment as described in Section 1.1 How is science done. But it is. Describe the discovery of pulsars (Hewish, A. et al., 1968, Nature 217, 709) in terms of the six experimental stages.
1.2 The significance of a certain conclusion depends very strongly on whether the most luminous known quasar is included in the dataset. The object is legitimately in the dataset in terms of pre-stated selection criteria. Is the conclusion robust? Believable?
2.1 A Warm-Up on Coin-Tossing. This is not an astronomical problem but does provide a warm-up exercise on probability and random numbers. Every computer has a way of producing a random number between zero and one. Use this to simulate a simple coin-tossing game where player A gets a point for heads, player B a point for tails. Guess how often in a game of N tosses the lead will change; if A is in the lead at toss N, when was the previous change of lead most likely to be? And by how much is a player typically in the lead? Try to back these guesses up with calculations, and then simulate the game. For many more game-based illustrations of probability, see Haigh, J., 1999, Taking Chances, Oxford University Press.
2.2 Efficient choosing. Imagine you are on a ten-night observing run with a colleague, in settled weather. You have an agreement that one of the nights, of your choosing, will be for your exclusive use. Show that, if you wait for five nights and then choose the first night that is better than any of the five, you have a 25 per cent chance of getting the best night of the ten. For a somewhat harder challenge, show that the optimum length of the "training sample" is a fraction 1/e of the total. Check your results with random-number generation.
2.3 Bayesian inference. Consider the proverbial bad penny, for which prior information has indicated that there is a probability of 0.99 that it is unbiased ("ok"); or a probability of 0.01 that it is double-headed ("dh"). What is the (Bayesian) posterior probability, given this information, of obtaining 7 heads in a row? In such a circumstance, how might we consider the fairness of the coin? Or of the experimenter who provided us with the prior information? What are the odds on the penny being fair?
2.4 Laplace's Rule and priors. Laplace's rule (Section 2.3) <ρ>=(N+1)/(N+M+2) depends on our prior for ρ. If we have one success and no failures, consider what the rule implies, and discuss why this is odd. How is the rule changed for alternative priors, for example Haldane's?
2.5 Bayesian reasoning in an everyday situation. The probability of a certain medical test being positive is 90 per cent, if the patient has disease D. If your doctor tells you the test is positive, what are your chances of having the disease? If your doctor also tells you that 1 per cent of the population have the disease, and that the test will record a false positive 10 per cent of the time, use Bayes' theorem to calculate the chance of having D if the test is positive. Simulate the experiment via Monte Carlo.
2.6 "Inverse" χ2 statistic. For a Gaussian of known mean (say zero), show that the posterior distribution for the variance is inverse χ2. Use the "Jeffreys Prior" for the variance: prob(σ)=1/σ. Comment on the differences between this result, and the one obtained by using a uniform prior on σ.
2.7 Maximum likelihood and the Poisson distribution. Suppose we have data which obey a Poisson distribution with parameter μ, and in successive identical intervals we observe n1, n2 ..... events. Form the likelihood function by taking the product of the distributions for each ni, and differentiate to find the maximum likelihood estimate of μ. Is it what you expect?
2.8 Maximum likelihood and the exponential distribution. Suppose we have data X1, X2 ..... from the distribution 1/2a e(-|x|/a). Compute the posterior distribution of a for a uniform prior, and Jeffreys's prior prob(a) α 1/a. Do the differences seem reasonable? Which prior would you choose? If a were known, but the location μ was to be found, what would be the maximum likelihood estimate?
2.9 Birth control. Imagine a society where boys and girls were (biologically) equally likely to be born, but families cease producing children after the birth of the first boy. Are there more males than females in the population? Attack the problem in three ways: pure thought, by a Monte Carlo simulation, and by an analytic calculation.
2.10 Univariate random numbers. Work out the inverses of the integral functions required to generate (a) f(x) = 2x3, (b) a power-law, representative of luminosity functions, f(x) = x-γ . Use these results to produce random experiments following these probabilities by drawing 1000 random samples uniformly distributed between 0 and 1; verify by comparison with the given functions.
3.1 Means and variances. Find the mean and variance of a Poisson distribution and of a power law; find the variance (= ∞) of a Cauchy distribution.
3.2 Simple error analysis. Derive the well known results for error combining, for two products, and the the sum and difference of two quantities, from the Taylor expansion of Section 3.3.2.
3.3 Combining Gaussian variables. Use the result of Section 3.3.2 for errors on z when z = x + y to find the distribution of the sum of two Gaussian variables. Test this with a Monte Carlo experiment.
3.4 Average of Cauchy variables. Show that the average value of Cauchy-distributed variables has the same distribution as the original data. Use characteristic functions and the convolution theorem.
3.5 Poisson statistics. Draw random numbers from Poisson distributions (Section 2.6) with μ = 10 and μ=100. Take 10 or 100 samples, find the average and the rms scatter. How close is the scatter to √μ?
3.6 Robust statistics. Make a Gaussian with outliers by combining two Gaussians, one of unit variance, one three times wider. Leave the relative weight of the wide Gaussian as a parameter. Compare the mean deviation with the rms, for various relative weights. How sensitive are the two measures of scatter to outliers? Repeat the exercise, with a width derived from order statistics. Check your results with a Monte Carlo experiment.
3.7 Change of Variable. Suppose that φ is uniformly distributed between zero and 2π. Find the distribution of sin φ. How could you find the distribution of a sum of sines of independent random angles?
3.8 Order statistics. We record a burst of N neutrinos from a supernova, and the probability of recording a neutrino at time t is, in suitable units, e(t-t0) where t0 is the time of emission. The maximum likelihood estimate of t0 is just T1, the time of arrival of the first neutrino. Use order statistics (Section 3.4) to show that the average value of T1 is just t0 + 1/N. Is this MLE biased, but consistent (i.e. the correct answer as N → ∞)?
4.1 Correlation testing (D). Consider the Hubble plot of Figure 4.3. What is (a) the most likely value for ρ via the Jeffreys test; (b) the significance of the correlation via the standard Fisher test, and (c) the significance via the Spearman rank test? Estimate distributions for these statistics with a bootstrap (Section 6.6); and compare the results with the standard tests.
4.2 Multivariate random numbers. (a) Give the justification for why the prescription (Section 6.5) for generating (X,Y) pairs following a Gaussian of given variance and correlation coefficient is correct. (b) Using a Gaussian Monte-Carlo generator, find 1000 (X,Y) pairs following a given prescription, i.e. σx2, σy2 and ρ. Plot these on contours of the bivariate probability distribution, as in Figure 6.2, to check roughly that the prescription works. (c) Find the error matrix for the (X,Y) pairs to verify that the prescription works.
4.3 Permutation tests (D). (a) Take a small set of uncorrelated pairs (X,Y), preferably non-Gaussian. By permutation methods on the computer, derive distributions of Fisher r, Spearman's and Kendall's statistics. (b) Try the same numerical experiment with correlated data, using the bootstrap and the jackknife to estimate distributions (Section 6.6). (Correlated non-Gaussian data are provided for the multivariate t-distribution, which is Cauchy-like for one degree of freedom and becomes more Gaussian for larger degrees of freedom.) How robust are the conclusions against outliers?
4.4 Principal-Component Analysis (D). Carry through a PCA on the data of the quasar sample given in Francis et al. 1999 (Francis, P.J. and Wills, B.J. 1999, in ASP Conf. Ser. 162: Quasars and Cosmology, p363). Compute errors with a bootstrap analysis or jackknife (Section 6.6).
4.5 Lurking third variables. Consider the following correlations, and speculate on how a third variable might be involved. (a) During the Second World War J.W. Tukey discovered a strong positive correlation between accuracy of bombing and the presence of enemy fighter planes. (b) There is a well-known correlation between stock market indices and the sunspot cycle. (c) The apparent angular size of radio sources shows a strong inverse correlation with radio luminosity.
5.1 Kolmogorov-Smirnov (D). Use the data provided, two datasets, one with a total of m = 290 observations, the other with 386 measurements. The former is of flux densities measured at random positions in the sky; the latter of flux densities at the positions of a specified set of galaxies. Using the Kolmogorov-Smirnov two-sample test, examine the hypothesis that there is excess flux density at the non-random positions.
5.2 Wilcoxon-Mann-Whitney (D). Repeat the test with the Wilcoxon-Mann-Whitney statistic. Is the significance level different? How would you combine the results from these two tests, plus the chi-square test in the text?
5.3 t-test and outliers (D). Create two datasets, one drawn from a Gaussian of unit variance, the other drawn from a variable combination of two Gaussians, the dominant one of unit variance and the other three times wider. All Gaussians are of zero mean. Perform a t-test on sets of 10 observations and investigate what happens as contamination from the wide Gaussian is increased. Compare the effect on the posterior distribution of the difference of the means. Now shift the narrow Gaussian by half a unit, and repeat the experiment. What effect do the outliers have on our ability to refute the null hypothesis? How does the Bayesian approach compare?
5.4 F-test (D). Create some random data, as in the first part of Exercise 5.3. Investigate the sensitivity of the standard F-test to a small level of contamination by outliers.
5.5 Non-parametric alternatives. (D) Repeat the analysis of the last two exercises, using a non-parametric test; the Wilcoxon-Mann-Whitney test for the location test, and the Kolmogorov-Smirnov test for the variance test. How do the results compare with the parametric tests? Can you detect genuine differences in variance, apart from the outliers?
5.6 Several datasets, one test. Suppose you have N independent datasets, and with a certain test you obtain a significance level of pi for each one. A useful overall significance is given by the W statistic (Peacock, J.A., 1985, Mon. Not. R. astr. Soc., 217, 601) which is
W=∏ pi, and the product is over i = 1 to N.
Find the distribution of logW and describe how it could be used. Note this contrasts to the case discussed in the text, where we might perform several different tests on the same dataset. (Each pi will be uniformly distributed between zero and one, under the null hypothesis. The distribution of logW is the sum of these uniformly distributed numbers, and tends to a Gaussian of mean N and variance N.)
5.7 Gram-Charlier (D). Take some data drawn from a Gaussian and investigate the posterior likelihood if just one term (the quadratic) is used in a Gram-Charlier expansion as an assumption for the "true" distribution. Take the location as known. Find the distribution of the variance, marginalizing out the Gram-Charlier parameter. Also, find the odds on including the parameter in the model. What does this tell you about assuming a Gaussian distribution when the amounts of data are limited?
5.8 Odds versus classical tests. Use the small dataset from the Example in Section 5.2.3. Perform a classical analysis, using t- and F-tests. Compare and contrast to the odds calculated in the text. Does the Behrens-Fisher distribution give a better answer than either or both? See Jaynes' comments on confidence intervals (Jaynes, E.T. 1983, Papers on Probability Theory, Statistics and Statistical Physics, Ed. Rosenkrantz, R.D. ESO Garching).
6.1 Covariance matrix. Consider N data Xi, drawn from a Gaussian of mean μ and standard deviation σ. Use maximum likelihood to find estimators of both μ and σ, and find the covariance matrix of these estimates.
6.2 Weighting data. Show that the optimum weight for an observation of standard deviation σ is just 1/σ2 . This weight turns up naturally in modelling using minimum-χ2.
6.3 MLE and power laws. In one example of Section 6.1 we fit a power law truncated at the faint end, and assume we know where to cut it off. What happens if you try to infer the faint-end cutoff by ML as well? Formulate this problem at least.
6.4 Maximum Likelihood estimators. Find an estimator of μ when the distribution is (a) prob(x) = exp [-|x-μ|] and (b) the Poisson prob(n) = μn e-μ / n!.
6.5 Least Squares linear fits. Derive the "minimum distance" OLS for errors in both x and y, assuming Gaussian errors.
6.6 Marginalization. Using the data supplied, use maximum likelihood to find the distribution of the parameters of a fitted Gaussian plus a baseline. Test to see how the estimates are affected by marginalizing out the baseline parameters.
6.7 The Jackknife and Bootstrap Methods. Using the MLE for a power-law index (Section 6.1), work out and compare the confidence intervals with the analytic result from that section using the jackknife and bootstrap tests. Check how the results depend on sample size.
7.1 Goodness-of-fit. A goodness-of-fit statistic, for example χ2, has a significance level p defined by p = ∫ f(χ2) dχ2 where the integral is defined from C to ∞, C is the observed value of χ2, and f is the appropriate distribution of χ2. Show that p is uniformly distributed if C is indeed drawn from f.
7.2 Monte Carlo integration. The Gaussian or Normal distribution function 1/(σ√ 2π) exp[ -x2 / 2σ2] does not have an analytic integral form. Use Monte Carlo integration to find erf, the so-called error function of Table A2.1. Show that (a) approximately 68 per cent of its area lies between ± σ, and (b) that the total area under the curve is unity.
7.3 Metropolis algorithm.Use the Metropolis algorithm to draw samples from a simple distribution, say the Laplacian exp | -x |. Check the match to the target distribution along the chain, using a selection of non-parametric tests (e.g. Kolmogorov-Smirnov).
7.4 Metropolis algorithm continued. Using the chains developed in Exercise 7.3, test the amount of correlation in the chain against various choices of the proposal distribution. Use the standard Fourier methods (Section 9.2) to do this, as outlined in this Chapter. Experiment with direct calculation of the correlation coefficient between elements of the chain separated by various amounts.
7.5 Burn-in.Using the chains of Exercise 7.3, make a direct check of the duration of burn-in by comparing with within-chain and between-chain variances.
7.6 Bayes Factor. A very common example of the issues around model complexity is given by the simple polynomial fit: adding another term to a polynomial often gives a better fit (smaller chi-square per degree of freedom) but introduces an additional parameter. Use some random data (say, 20 numbers drawn from a Gaussian distribution) and the Bayes factor method to examine the odds in favour of adding one more polynomial term. Test that the Laplace approximation can be used to avoid a multi-dimensional numerical integration.
7.7 Markov-Chain Monte-Carlo. Extend the previous Exercise to compute the actual posterior probabilities for three possible polynomials from a constant through to a quadratic. In this case the evidence will have to be calculated: use a MCMC method to compute the evidence by a thermodynamic integration.
7.8 Consistency of Observations. Refer to Press's paper (Press, W.H., 1997, in Unsolved Problems in Astrophysics, ed. J.N. Bahcall & J.P. Ostriker, Princeton University Press, 49) to derive the formula quoted in the text for the probability of a given observation being `good'.
8.1 Source counts and luminosity function. Derive the relationship between the number count and the luminosity function for a general luminosity function; show that the result takes a simple form for a power-law luminosity function.
8.2 Noise and source-count slope. Generate data from a power-law source count and add noise; by a maximum-likelihood fit, investigate the effect of the noise level on the inferred source-count slope. Use the results from Exercise 8.1 to show the effect of the noise on the luminosity function.
8.3 Survey completeness and noise. Make a 1-D Gaussian signal plus noise plus baseline, fit a profile, verify completeness versus signal-to-noise ratio. Do the same for an empty field.
8.4 Reliability and completeness. Calculate the relationship between reliability and completeness for an exponential noise distribution. This shows the effect of wide wings on the noise distribution. Compare with the result for a Gaussian.
8.5 Vmax method (D). Simulate a flux-limited sample of galaxies by populating a large volume of space with galaxies drawn from a Schechter distribution. (The cumulative form of the Schechter distribution is rather complicated so you may prefer to use a power law.) Apply the Vmax method and see if you can recover the input distribution. Check the simple √N error bars against repeated runs of the simulation.
8.6 Error estimates (D). Adapt the simulation of Exercise 8.5 to produce bootstrap error estimates. Compare these with √N and Monte Carlo estimates, especially for the case of few objects per bin. (The data here are the same as for 8.5)
8.7 Luminosity-distance `correlation' (D). Adapt the simulation of Exercise 8.5 to the case for which each galaxy has two independent luminosities assigned to it (at different wavelengths, say). Check that these luminosities show a bogus correlation unless upper limits are included in the analysis. Adapt the simulation to produce intrinsically-correlated luminosities and show that the Kendall test can detect these correlations. (The data here are the same as for 8.5)
8.8 Parameter error estimates. Use the X-ray and radio data from Avni et al. (Avni, Y., Soltan, A., Tananbaum, H. and Zamorani, G., 1980, Astrophys. J., 238, 800) as given in the example in the text, to work out the mean spectral index in their survey. Using their likelihood function as a starting point, work out error bounds on the mean, using a likelihood ratio. You will need to use a Lagrange multiplier in the maximization of the likelihood.
8.9 Source counts from confusion (D). In a confusion-limited survey where there are potentially several sources per beam, the apparent source count can be very different from the true one. On the assumption that sources can lie anywhere in the beam and are not clustered, derive the result for the source count.
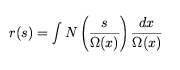
as given in Section 8.6.
8.10 Monte Carlo and confusion. Design your own confusion-limit experiment. Use a version of the toy universe to derive a source count: produce a patch of sky like that of Figure 2.10; pick a beam size such that your sky survey becomes totally confusion limited; convolve the points in the patch of sky with your beam; compile a p(D) distribution of at least 1000 samples more than one beam area apart; analyse this distribution to find parameters which describe the count below the confusion limit; assess errors; compare with the source count originally prescribed for the source population.
9.1 Fourier transform and FFT. Use a direct numerical integration to do a numerical Fourier transform of an oscillatory function, say a sine wave or a Bessel function. Compare the timings with an off-the-shelf FFT routine, checking how many oscillations you can fit in your region of integration before the FFT accelerates away from the direct method.
9.2 Wiener filtering and 1/f noise (D). Make some synthetic data along the lines of the example in Figure 9.1, and make it work with a Wiener filter for uncorrelated Gaussian noise. Now generate some 1/f noise. Add this in to the input spectrum, and perform the filtering again, without taking account of the extra low-frequency noise in the form of the Wiener filter. Does the 1/f noise affect (a) the line profile parameters (b) the baseline parameters?
9.3 Periodogram (D). Consider the Lomb-Scargle periodogram method as formulated by Press et al. (Press, W.H., Teukolsky, S.A., Vettering, W.T. and Flannery, B.P., 2007, Numerical Recipes, CUP); use the Numerical Recipes routines to test the following issues.
a) If we can sample at much above the pseudo-Nyquist rate, how much? Where does this run out? Why in practice can we not realize the sampling at these high frequencies provided by scattered time measurement?
b) The lines of probability in Figure 9.5 are roughly correct for the random uniform coverage of the left set of data. For the data on the right, uniformity has been assumed and the probabilities in the diagram are incorrect. Use the Numerical Recipes routine and the Monte-Carlo technique outlined to determine how they should be adjusted.
9.4 Properties of the power spectrum of periodic data. From the max/min statistics analysis of Section 3.4:
a) Find the probability density function equivalent to equation 7.11 for minimum values.
b) Show that the peak of the distribution function of the max in the power spectrum of data N long is ln(N).
9.5 Power spectrum of signal + noise. For a signal containing a deterministic signal S and Gaussian noise x, show that the noise distribution in each component of the power spectrum is in general a non-trivial combination of χ2 and Gaussian noise.
9.6 1/f noise. Harmonic analysis (sampling, Fourier transforming) of Beethoven's symphonies indicate that their power spectra follow the 1/f law to a good approximation. Consider why this should be so. See Press 1978 (Press, W.H., 1978, Comments Astrophys., 7, 103) for a few hints.
Example piece of rock
Jazz phases, rock amplitudes combined
Rock phases, jazz amplitudes combined
9.7 Filtering and mean values. Take your favourite implementation of the FFT, and form the power spectrum of a scan consisting entirely of uncorrelated Gaussian noise. Integrate the power spectrum; is the answer the variance of the input data? If not, why not? Now convolve the data with your favourite (normalized) filter. From the zero frequency of the power spectrum, what is the variance in the mean? Does it change if you change the width of the filter? Explain.
9.8 Baselines (D). Fit a Fourier baseline interactively to a spectrum containing a moderately obvious but contaminated line. Now, separately, fit a Gaussian to the line and give your best estimate of the uncertainty in the total flux in the line. Compare this with a complete Bayesian analysis, fitting the same number of harmonics plus Gaussian ab initio, and then marginalizing out the baseline parameters.
10.1 Rayleigh's test. Why should the test statistic for Rayleigh's test be asymptotically χ2? Compute the statistic for small numbers, say <10; see Section 3.3.3.
10.2 Variance of estimators for w(θ) (D). Generate 20,000 data points randomly in the region 00 < α < 50, 00 < δ < 50. Estimate w(θ) using the Natural estimator w1, the Peebles estimator w2, the Landy-Szalay estimator w3 and the Hamilton estimator w4. (Average DR and RR over say 10 comparison sets each of 20,000 random points). Plot the results as a function of δ showing Poisson error bars 1/√DD. Comment on the results - which estimator is best?
10.3 Integral constraint on w(θ). (a) Show that the factor C in equation 9.27 is 1/(1+W) where W = ∫ w(θ) dGp. (b) Derive an approximate expression for W, assuming a power-law form for w(θ) = (θ / θ0)-b.
10.4 The effect of surface density changes on w(θ) (D). (a) Estimate the magnitude of the offset in w(θ) taking a simple model in which a survey is divided into two equal areas between which there is a fractional surface density shift ε (Equation 9.29). Find the expected step in w(θ) as a function of ε; verify that a step of 20 per cent results in Δw = 0.01. (b) Confirm this prediction with a toy-model simulation, putting say 100,000 random points in the region 00 < α < 600, -200 < δ < +200 with a 20 per cent step at δ = 00. Then calculate the w(θ) using say Landy-Szalay (w4) estimator over the small-angular-scale range θ < 10, checking that w(θ) agrees within errors with the prediction from equation 9.29.
10.5 The effect of surface-density changes on c-in-c (D). (a) Use the 100,000 random points generated in the region 00 < α < 600, -200 < δ < +200 for Exercise 10.4. Generate a set of 10 grid patterns for circular non-overlapping cells over the area, with diameter 0.030 to 30, evenly spaced in logθ. Compile P(N) for each of these and show that the means and variances are as expected for Poissonian distributions. Calculate and plot the variance statistic y(L) (equation 10.15) as a function of cell size; verify that there is no significant offset from zero. (b) Put in a 20 per cent step in surface density, dividing the field in half at δ = 00. Recalculate the y(L) and verify that the apparent offset in y(L) is of the expected magnitude Δy = 0.01 (equation 10.25).
10.6 w(θ) and the angular power spectrum (D). Simulate a square piece of sky 100 x 100 , using 10000 points placed at random. (a) Verify that there is no significant signal either in w(θ) or in the angular power spectrum. (b) Build a hierarchy of galaxy clusters and clusters of clusters using perhaps another 10000 points, adopting Gaussian shapes for clusters, cluster-clusters, etc. (c) Show that with a few adjustments to the parameters (see Figure 10.2), it is possible to produce an approximate power law of slope ~-1 for a single hierarchy of clustering. Relate the resultant form of the angular power spectrum and its information content to this w(θ).